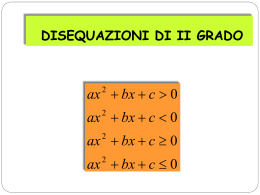
DISEQUAZIONI INTERE
DI 2° GRADO
ax  bx  c  0
2
ax  bx  c  0
2
ax  bx  c  0
2
ax  bx  c  0
2
Prof. V. Scaccianoce
Esempio 1
x  14 x  13  0
2
Si considera l’equazione associata
x  14 x  13  0
2
Prof. V. Scaccianoce
x 2  14 x  13  0
Si risolve, trovando le eventuali
soluzioni
x
0
14  196  4 1  13
2
14  144
x
2
Prof. V. Scaccianoce
14  12

2
x1  1
Prof. V. Scaccianoce
x2  13
x 1
x  13
Si posizionano le soluzioni sopra
una retta orientata.
1
Prof. V. Scaccianoce
13
1x -14x +13 > 0
2
Si disegna la parabola che passa
per i punti trovati e,
poiché il primo coefficiente a è
positivo,
avente la concavità verso l’alto.
1
Prof. V. Scaccianoce
13
x 2  14 x  13  0
Poiché nella disequazione si è
interessati a quella parte di parabola
positiva,
>0
1
Prof. V. Scaccianoce
13
Si evidenzia la parte della parabola
e si proiettano sulla retta i punti
corrispondenti.
>0
1
Prof. V. Scaccianoce
13
x -14x +13 > 0
2
L’insieme dei punti che soddisfa la
disequazione data è costituita dai
numeri tali che:
x  13
x 1
1
Prof. V. Scaccianoce
13
Esempio 2
x  6x  9  0
2
Si considera l’equazione associata
x  6x  9  0
2
Prof. V. Scaccianoce
x  6x  9  0
2
Si risolve, trovando le eventuali soluzioni
6  36  4 1 9
x
2
0
6 0
x
2
Prof. V. Scaccianoce
60
x
2
x3
x3
SOLUZIONI REALI E COINCIDENTI
Prof. V. Scaccianoce
x3
Si posiziona l’unica soluzione
sopra una retta orientata.
3
Prof. V. Scaccianoce
1x  6 x  9  0
2
Si disegna la parabola che passa
per il punto trovato e,
poiché il primo coefficiente a è
positivo,
avente la concavità verso l’alto.
3
Prof. V. Scaccianoce
x2  6x  9  0
Poiché nella disequazione si è
interessati a quella parte di
parabola positiva,
>0
3
Prof. V. Scaccianoce
Si evidenzia la parte della parabola
e si proiettano sulla retta i punti
corrispondenti.
>0
Prof. V. Scaccianoce
3
x2  6x  9  0
L’insieme dei punti che soddisfa la
disequazione data è costituita dai
numeri tali che:
x3
x3
3
ossia
Prof. V. Scaccianoce
x  R  3
Esempio 3
x  2x  5  0
2
Si considera l’equazione associata
x  2x  5  0
2
Prof. V. Scaccianoce
x2  2x  5  0
Si risolve, trovando le eventuali soluzioni
2  4  4 1 5
x
2
  0 x  2   16
2
Prof. V. Scaccianoce
NON ESISTONO SOLUZIONI REALI
Pertanto non si possono posizionare
le soluzioni sopra la retta orientata.
Prof. V. Scaccianoce
1x  2 x  5  0
2
Si disegna una parabola che
non tocca la retta e,
poiché il primo coefficiente
a è positivo,
avente la concavità verso l’alto.
Prof. V. Scaccianoce
x2  2x  5  0
Poiché nella disequazione si è
interessati a quella parte di
parabola positiva,
>0
Prof. V. Scaccianoce
Si evidenzia la parte della
parabola
e si proiettano sulla retta i punti
corrispondenti.
>0
Prof. V. Scaccianoce
x2  2x  5  0
L’insieme dei punti che soddisfa la
disequazione data è costituita ...
….da tutti i numeri reali
ossia
Prof. V. Scaccianoce
SR