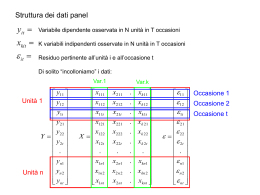
Struttura dei dati panel
yit 
Variabile dipendente osservata in N unità in T occasioni
xkit 
K variabili indipendenti osservate in N unità in T occasioni
 it 
Residuo pertinente all’unità i e all’occasione t
Di solito “incolloniamo” i dati:
Var.1
 y11 
y 
Unità 1
 12 
 y1t 
 
 y21 
 y22 
Y  
 y2t 
 . 
 
 yn1 
 
Unità n  yn 2 
 ynt 
 x111
x
 112
 x11t

 x121
 x122
X 
 x12t
 .

 x1n1
x
 1n 2
 x1nt
Var.k
x211
.
x212
.
x21t
.
x221
.
x222
x22t
.
.
.
.
x2 n1
.
x2 n 2
x2 nt
.
.
xk11 
xk 12 
xk1t 

xk 21 
xk 22 

xk 2 t 
. 

xkn1 
xkn 2 

xknt 
 11  Occasione 1
 
 12  Occasione 2
 1t  Occasione t
 
 21 
 22 
  
  2t 
 . 
 
  n1 
 
 n2 
  nt 
Vediamo un esempio:
60
C=40+0.45 R
50
C=30+0.45 R
Consumi
40
30
C=20+0.45 R
20
C=10+0.45 R
10
C=1.5+4.12 R
0
0
5
10
15
Reddito
Stessa “pendenza” diverse “intercette”!!!!
20
25
In altri termini la elasticità del consumo rispetto al reddito
sono le stesse per tutti gli individui,
ciò che cambia è il “punto di partenza, cioè il consumo
che corrisponde ad un reddito 0
I dati sezionali “nascondono” questo fatto:
Sottostimano il “punto di partenza” (l’intercetta)
Sovrastimano l’elasticità (la pendenza)
Vi è Distorsione: essa distorsione si annulla solo se
l’intercetta per ogni individuo è la STESSA
Cioè una stima sezionale ipotizza un MODELLO di
comportamento in cui la parte non spiegata della
relazione (l’intercetta) è la stessa per tutti gli individui
Cioè nega l’ETEROGENEITA’ tra individui
1) E’ venuta alla luce una ipotesi del modello che non era
stata esplicitata: l’omogeneità tra le parti non osservate di
ciascun individuo.
2) Solo una certa configurazione dei dati (osservazioni in
più occasioni) consente di esplicitare ed affrontare
l’eterogeneità
3) Il modo in cui rappresentiamo con dati (simboli) il
fenomeno (modello) hanno una influenza diretta sulle
leggi che regolano il linguaggio (la tecnica ) e quindi
sulle conclusioni
4) Dobbiamo sempre occuparci del processo che ha
generato i dati che può non essere neutrale per il modello
Casistica di non neutralità delle misure.
Consideriamo un collettivo di unità statistiche, il DGP ha tra le sue
caratteristiche più importanti la relazione (se c’è) che lega le
misure effettuate sulle diverse unità. La casistica possibile è
ampia, tra le assunzioni più comuni:
1. Indipendenza (nota e utile, tuttavia un DGP poco verosimile: ad
es: imprese di uno stesso settore, pazienti di una stessa città….)
2. Di solito misure ripetute relative ad una stessa unità sono più
“simili” di quelle tra unità diverse
3. Di solito misure vicine nel tempo e nello spazio tendono ad
essere più simili di quelle più lontane
Un problema dei dati sezionali:
l’eterogeneità non osservata
•Molte caratteristiche individuali non sono osservate, alcune sono
anche non osservabili (es. Capacità imprenditoriale, entusiasmo,
propensione al rischio)
•Queste variano tra gli individui e sono denominate “eterogeneità
non osservata”
•Se queste caratteristiche sono correlate con la variabile di interesse
e/o con le variabili osservate, allora la stima dei coefficienti è
DISTORTA
•DISTORSIONE DA VARIABILE OMESSA.
•I dati di panel consentono di correggere questo BIAS
(digressione sulle variabili omesse)
Supponiamo che il modello “vero” sia (in forma vettoriale):
y  X11  X 2 2  
Se ignoriamo X2

b1  X 1 X 1'
sarà

1

X 1' y  1  X 1 X 1'

Eb1   1  X 1 X

' 1
1

1

X 1' X 2  2  X 1 X 1'

1
X 1'
X 1' X 2  2  1  P1.2  2
La matrice P contiene le pendenze OLS di X2 su X1. Ad esempio nella relazione
consumo   * prezzo   * reddito
sia reddito   * prezzo
ignorando il
reddito :
Eb       
Cov( prezzo , reddito)

Var ( prezzo )
Sulla matrice di var-covar il discorso è più complesso:
X X 
Var (b )   X MX 
con M  I  X X X 
Var (b1 )  
' 1
1
2
1
' 1
1
2
1.2
1
2
2
' 1
2
X 2'
cioè

 1 
1
Varb1   Var (b1.2 ) 1   2  X 1' X 2 X 2 X 2'
 

1
X 2' X 1
Con due variabili:
Var (b1 ) 
2
con
s11
Var (b1.2 ) 
2

s11 1  r122

s11    xi1  x1 
2
con
r122  correl ( x1 x2 )
Distorsione nella stima sia sui coefficienti che sulla Var
Dobbiamo specificare la forma della eterogeneità, ciò implica ipotesi sulla
matrice di varianza-covarianza, cioè sulla struttura dei residui del modello
In generale le varianze dei (residui) del modello non saranno omoschedastiche
saranno caratterizzate da diverse componenti che vanno “scorporate” in modo
ottenere stime corrette.
Questo tipologia di modelli è detta “a componenti di varianza”.
Naturalmente si avranno diversi tipi di modelli a seconda delle ipotesi
sulle componenti di varianza che potranno essere, in prima istanza,
di tipo deterministico o stocastico
Un discorso analogo vale anche per la Covarianza che, però, definisce modelli
Diversi, in gran parte legati alla analisi di serie storiche
Un esempio Costi e produzione di 6 imprese per 4 anni:
I DATI
impresa
1
2
3
4
5
6
t=1
3,5
3,9
19,0
35,2
33,2
73,1
Costi (Y)
Produzione (X)
t=2
t=3
t=4
t=1
t=2
t=3
t=4
4,3
4,6
5,8
214
419
588 1025
5,5
8,1 16,4
696
811 1640 2506
26,0
32,4 44,7 3202 4802 5821 9275
51,1
61,0 77,9 5668 7612 10206 13702
40,0
43,1 57,7 6000 8222 8484 10004
98,8 138,9 191,6 11796 15551 27218 30958
LOGARITMI:
impresa
1
2
3
4
5
6
t=1
1,25
1,35
2,95
3,56
3,50
4,29
Costi (Y)
t=2
t=3
1,45 1,52
1,71 2,10
3,26 3,48
3,93 4,11
3,69 3,76
4,59 4,93
t=4
1,77
2,80
3,80
4,36
4,06
5,26
Produzione (X)
t=1
t=2
t=3
t=4
5,37 6,04
6,38 6,93
6,55 6,70
7,40 7,83
8,07 8,48
8,67 9,14
8,64 8,94
9,23 9,53
8,70 9,01
9,05 9,21
9,38 9,65 10,21 10,34
Adattiamo un modello lineare:
OLS: a=-4.18
b=0.89
ln(Y)=a+bln(X)+
Var=0.04
r²=0.98
7
6
5
Impr.1
Impr.2
4
Impr.3
Impr.4
3
Impr.5
Impr.6
Stima
2
1
0
4
5
6
7
8
9
10
11
12
13
Abbiamo una PRIMA stima del modello quindi possiamo stimare i residui
eˆi ,t  yi ,t    xi ,t
E dai residui Varianze individuali e correlazioni
Ovviamente dobbiamo ipotizzare una “forma” per Varianze e Covarianze
IPOTESI:
Per le varianze individuali: Costanti nel tempo
Per le correlazioni: processo AR(1)
• Sotto queste ipotesi la stima è possibile mediando (rispetto al tempo)
i quadrati dei residui per ogni individuo
T
 i2 
2
ˆ
e
 it
t 1
T
•Calcolando l’autocorrelazione con lag=1
 eˆ
T

eˆ
i ,t i ,t 1
t 2
 eˆ 
T
t 2
2
i ,t

Consideriamo i residui per per ciascuna impresa:
t=1
t=2
t=3
t=4
t=1
t=2
t=3
t=4
t=1
t=2
t=3
t=4
t=1
t=2
t=3
t=4
t=1
t=2
t=3
t=4
t=1
t=2
t=3
t=4
y
x
1,25 5,37
1,45 6,04
1,52 6,38
1,77 6,93
1,35 6,55
1,71 6,70
2,10 7,40
2,80 7,83
2,95 8,07
3,26 8,48
3,48 8,67
3,80 9,14
3,56 8,64
3,93 8,94
4,11 9,23
4,36 9,53
3,50 8,70
3,69 9,01
3,76 9,05
4,06 9,21
4,29 9,38
4,59 9,65
4,93 10,21
5,26 10,34
y*
0,65
1,23
1,53
2,02
1,68
1,81
2,43
2,81
3,02
3,38
3,54
3,96
3,52
3,78
4,04
4,30
3,57
3,84
3,88
4,02
4,17
4,41
4,90
5,01
e
-0,60
-0,22
0,01
0,25
0,33
0,10
0,33
0,01
0,07
0,12
0,06
0,16
-0,04
-0,15
-0,07
-0,06
0,07
0,15
0,12
-0,04
-0,12
-0,18
-0,03
-0,25
Var
correl
0,13
0,99
0,03
-0,95
0,00
-0,92
0,00
-0,62
0,01
-0,25
0,01
-0,95
Scopriamo che le varianze per impresa sono diverse cioè c’è eteroschedasticità:
(significatività test F per l’uguaglianza delle varianze)
impresa1 impresa2
impresa3 impresa4 impresa5 impresa6 overall
impresa1
1,000
0,225
0,006
0,007
0,039
0,050
0,083
impresa2
0,225
1,000
0,060
0,069
0,307
0,369
0,828
impresa3
0,006
0,060
1,000
0,934
0,317
0,262
0,029
impresa4
impresa5
0,007
0,039
0,069
0,307
0,934
0,317
1,000
0,356
0,356
1,000
0,295
0,894
0,034
0,176
impresa6
0,050
0,369
0,262
0,295
0,894
1,000
0,220
E che le autocorrelazioni tra i residui della stessa impresa sono MOLTO diverse da 0
impresa1
0,99
impresa2
-0,95
impresa3
-0,92
impresa4
impresa5
-0,62
-0,25
impresa6
-0,95
Infatti se utilizziamo GLS (con stima elementare della matrice Var/covar)
(varianze residui sulla diagonale e AR1 nei blocchi di impresa)
0,05
0,83
0,69
0,48
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,83
0,05
0,83
0,69
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,69
0,83
0,05
0,83
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,48
0,69
0,83
0,05
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,39
0,99
0,98
0,96
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,99
0,39
0,99
0,98
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,98
0,99
0,39
0,99
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,96
0,98
0,99
0,39
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,13
0,98
0,96
0,92
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,98
0,13
0,98
0,96
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,96
0,98
0,13
0,98
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,92
0,96
0,98
0,13
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,11
0,96
0,92
0,84
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,96
0,11
0,96
0,92
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,92
0,96
0,11
0,96
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,84
0,92
0,96
0,11
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,05
0,82
0,68
0,46
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,82
0,05
0,82
0,68
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,68
0,82
0,05
0,82
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,46
0,68
0,82
0,05
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,18
1,00
1,00
1,00
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1,00
0,18
1,00
1,00
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1,00
1,00
0,18
1,00
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1,00
1,00
1,00
0,18
Otteniamo stime diverse per i coefficienti:
a= -5.91 b=1.10
NB. Non è stima FGLS! Dimostra solo che
i residui non sono omoschedastici e incorrelati
Avvertenze sulla notazione:
D’ora in poi i simboli utilizzati nella notazione indicheranno VETTORI/MATRICI
Per i residui, in generale
il simbolo u indicherà residui OMOSCHEDASTICI e INCORRELATI
Il simbolo  indicherà un residuo “composto” da u e una componente
ETEROSCHEDASTICA e/o correlata, DETERMINISTICA o STOCASTICA
A questo punto dobbiamo modificare il modello semplice:
Formuliamo una ipotesi di dipendenza:
yit  f ( x1it , x2it ,..., xkit )
Sviluppiamo un modello: (a componenti di varianza)
yit   0   ' xit   it
Variabili
esplicative
 it  i  uit
Errore “Composto”
uit ~ N (0,  u2 )
Componente individuale
Deterministica o stocastica
Costante nel tempo
Diversi modi per specificare l’errore
(ce ne sono altri…)
 it  i  uit
Effetto
Individuale
Effetto
temporale
 it  i  t  uit
Errore
casuale
Effetto individuale
Due possibilità di trattamento (due dgp):
• Effetti FISSI: i sono constanti e vengono trattati come una
intercetta
yit   0  i    ' xit  uit
• Effetti CASUALI: i sono estrazioni da una distribuzione di
probabilità data e diventano componenti stocastiche dell’errore,
cioè i i hanno una “loro” varianza
yit   0   ' x1it  (i  uit )
Il Modello “zero” nessun effetto
Pooled regression
• Si suppone che non vi sia eterogeneità o che l’eterogeneità sia
stata eliminata in qualche modo: i sono constanti tra gli individui e
identificano una UNICA intercetta.
• Le procedure di stima possibili si differenziano per il trattamento
“preliminare dei dati:
• OLS “usuale” sui dati non trattati :
• OLS sugli scarti per ciascun individuo (stima within)
• OLS sulle medie (nel tempo) di ciascun individuo (stima between)
• Altri trattamenti (ad. Es. Sulle variazioni nel tempo)
Prima strategia :OLS “usuale”
yit   0   ' xit   it
E ( it | xit )  0
Var ( it | xit )   2
i, t
Cov( it ,  js | xit , x js )  0 per i  j or t  s
Attenzione agli indici nelle ipotesi sulla varianza/covarianza:
Per la Var si ipotizza che i residui siano omoschedastici per ogni individuo e per ogni occasione
Per la Covar si suppone pari a 0 in ogni individuo e in ogni occasione
Naturalmente se c’è effetto individuale
Si ottiene stima distorta
Modello “vero”
yit   0  i    ' xit   it
Modello stimato
Con (ci torneremo)
Si ha:
yit   0   ' xit  uit
E (i | xit )   0
yit   0   ' xit   it  i  E (i | xi ) 
yit   0   ' xit   it  ui
yit   0   ' xit  wit
Quindi il residuo stimato non è  ed ha una componente u che si “ripete” nel
tempo per lo stesso individuo, quindi è ETEROSCHEDASTCO e
CORRELATO (nel tempo sullo stesso individuo)
Seconda strategia : stimatore within:
OLS sugli scarti dalla media calcolata in t per ciascun i
( yit  yi. )   xit  xi.    it   i. 
ma
 it   i.   i  uit   i  ui.   i  i  uit  ui. 
In questo caso i i vengono eliminati e con essi la distorsione nella
stima, ma non abbiamo stime per le intercette individuali.
Quindi avremo problemi, ad esempio in termini di previsione.
Terza strategia : stimatore between
OLS sulle media calcolata in t per ciascun i
yi.  xi.   i.
Stessi problemi del modello OLS “usuale per quanto riguarda la
distorsione,
In più forte perdita di dati, quindi perdita di efficienza
Altre strategie: stimatore alle differenze prime
OLS sulle variazioni t per ciascun i
yit   yit  yi ,t 1 
xit  xit  xi ,t 1 
yit  i   ' xit    it
yit   ' xit   uit
 it   it   i ,t 1 
i i vengono eliminati e con essi la distorsione nella
stima,
ma non è una strategia raccomandabile, ad esempio
elimina tutte le variabili esplicative “time invariant”
Cioè modifica la specificazione del modello
Effetti FISSI
Abbiamo visto che alcune strategie eliminano le distorsoni ma, quantomeno, non
forniscono una stima delle intercette individuali
Occupiamoci, ora, esplicitamente della stima dei i
cominciando dal caso in cui essi siano deterministici, cioè costanti nel tempo e
variabili tra gli individui
Stima delle intercette individuali:
Least Square Dummy Variables (LSDV)
I metodi di eliminazione non stimano i i,cioè non forniscono una
misura delle caratteristiche non osservate.
Se si è interessati alla stima dei i è necessario adottare un altro
stimatore.:
 y11 
y 
 12 
 y1t 
 
 y21 
 y22 
Y  
 y2t 
 . 
 
 yn1 
y 
 n2 
 ynt 
1
1

1

0
0
X 
0


0
0

0
0 0
0 0
0 0
1 0
1 0
1 0
.
0 1
0 1
0 1
x211 . xk11 
x212 . xk12 
x21t . xk1t 

x221 . xk 21 
x222 . xk 22 

x22t . xk 2t 
. 
.
.

x2 n1 . xkn1 
x2 n 2 . xkn 2 

x2 nt . xknt 
  11 
 
 12 
  1t 
 
 21 
 22 
  
  2t 
 . 
 
  n1 
 
 n2 
  nt 
Riassumendo: EFFETTI FISSI
4 stimatori
pooled
yit   0  xit   it
within ( yit  yi )   xit  xi   uit
between yi  xi   i
LSDV
yit   0  i  xit  uit
Stimatore "overall"
70
y = 3,4975x + 6,2438
2
R = 0,8331
60
50
y
40
30
20
10
0
0
2
4
6
8
10
x
12
14
16
18
Stimatore "overall" RESIDUI
20
15
10
y residuo
5
ind1
ind2
0
0
2
4
6
8
10
12
14
16
18
ind3
ind4
-5
-10
-15
-20
x
Stimatore "within"
5
y = 0,7691x + 7E-16
4
R2 = 0,5272
3
2
1
y
0
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
-5
x
1
2
3
4
5
Stimatore "within" RESIDUI
4
3
2
1
y
0
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
x
1
2
3
4
5
Stimatore "beetween"
60
y = 4,1195x + 1,5372
R2 = 0,9927
50
y
40
30
20
10
0
0
2
4
6
8
x
10
12
14
Stimatore "LSDV"
60
50
y
40
30
Y= 10,6+0,77 X +10,6 ind2 +21,6 ind3 +32,7 ind4
r²=0,99
20
10
0
0
2
4
6
8
10
x
12
14
16
18
Stimatore "LSDV residui"
4
3
2
y
1
0
0
2
4
6
8
10
-1
-2
-3
-4
x
12
14
16
18
I coefficienti della X
Pooled
3.4974
Within
0.7691
Between
4.1195
LSDV
0.7691
2 considerazioni:
1. LSDV=Within per quanto riguarda le “pendenze
2. Overall = media ponderata (within e between)
Abbiamo visto che 3 delle strategie proposte hanno diversi
limiti, tuttavia esse rimangono importanti perché forniscono
la base per test inferenziali sul modello LSDV
Infatti collegati a ciascuna strategia è possibile ottenere una
valutazione dell’errore di stima fondata sulle ipotesi di
ciascuna strategia
Tali quantità si prestano ad un insieme di test,
sostanzialmente ispirati dallo schema di Analisi della
varianza.
Esempio e test di ipotesi
Procedimento:
1 calcolo RSS per il modello within
2. Calcolo RSS per il modello “totale”
3 Trovo per differenza RSS between
NB. Dati lievemente diversi
Rispetto all’esempio precedente
I DATI
impresa
1
2
3
4
5
6
Costi (Y)
Produzione (X)
t=1 t=2 t=3 t=4 t=1
t=2
t=3
t=4
3,2 4,3 4,6 5,8
214
419
588 1025
3,9 5,5 8,1 11
696
811 1640 2506
19 26 32 41 3202 4802 5821 9275
35 51 61 78 5668 7612 10206 13702
33 40 43 58 6000 8222 8484 10004
73 99 139 192 11796 15551 27218 30958
LOGARITMI:
impresa
1
2
3
4
5
6
t=1
1,2
1,4
3
3,6
3,5
4,3
Y
t=2 t=3 t=4
1,5 1,5 1,8
1,7 2,1 2,4
3,3 3,5 3,7
3,9 4,1 4,4
3,7 3,8 4,1
4,6 4,9 5,3
MEDIE PER INDIVIDUO:
impresa
1
2
3
4
5
6
Totale
Y
1,5
1,9
3,4
4
3,8
4,8
3,2
X
6,2
7,1
8,6
9,1
9
9,9
8,3
X
t=1
5,37
6,55
8,07
8,64
8,7
9,38
t=2
t=3
t=4
6,04 6,38 6,93
6,7
7,4 7,83
8,48 8,67 9,14
8,94 9,23 9,53
9,01 9,05 9,21
9,65 10,21 10,34
Stima within: incolonniamo i
dati:
Dati
impres Occas
a
.
1
1
1
2
1
3
1
4
2
1
2
2
2
3
2
4
3
1
3
2
3
3
3
4
4
1
4
2
4
3
4
4
5
1
5
2
5
3
5
4
6
1
6
2
6
3
6
4
Y
1,15
1,45
1,52
1,77
1,35
1,71
2,1
2,39
2,95
3,26
3,48
3,72
3,56
3,93
4,11
4,36
3,5
3,69
3,76
4,06
4,29
4,59
4,93
5,26
Stima within: a
b
Media di impresa
X
5,37
6,04
6,38
6,93
6,55
6,7
7,4
7,83
8,07
8,48
8,67
9,14
8,64
8,94
9,23
9,53
8,7
9,01
9,05
9,21
9,38
9,65
10,21
10,34
Y
1,47
1,47
1,47
1,47
1,89
1,89
1,89
1,89
3,35
3,35
3,35
3,35
3,99
3,99
3,99
3,99
3,75
3,75
3,75
3,75
4,77
4,77
4,77
4,77
X
6,18
6,18
6,18
6,18
7,12
7,12
7,12
7,12
8,59
8,59
8,59
8,59
9,09
9,09
9,09
9,09
8,99
8,99
8,99
8,99
9,90
9,90
9,90
9,90
-3,79E-16
0,676531
Scarti
impresa
Y
-0,32
-0,02
0,05
0,30
-0,54
-0,18
0,21
0,50
-0,40
-0,09
0,13
0,37
-0,43
-0,06
0,12
0,37
-0,25
-0,06
0,01
0,31
-0,48
-0,18
0,16
0,49
X
-0,81
-0,14
0,20
0,75
-0,57
-0,42
0,28
0,71
-0,52
-0,11
0,08
0,55
-0,44
-0,15
0,15
0,45
-0,29
0,02
0,06
0,22
-0,51
-0,24
0,32
0,45
RSS within=
Residu
i
Residui^2
0,23
0,05
0,07
0,01
-0,09
0,01
-0,21
0,04
-0,15
0,02
0,11
0,01
0,02
0,00
0,02
0,00
-0,05
0,00
-0,02
0,00
0,07
0,01
0,00
0,00
-0,13
0,02
0,04
0,00
0,02
0,00
0,07
0,00
-0,05
0,00
-0,07
0,01
-0,03
0,00
0,16
0,03
-0,13
0,02
-0,01
0,00
-0,05
0,00
0,19
0,04
0,266
Stima “Overall”:
incolonniamo i dati:
Stima within: a
b
media
"totale"
Dati
impre Occas
sa
.
1
1
1
2
1
3
1
4
2
1
2
2
2
3
2
4
3
1
3
2
3
3
3
4
4
1
4
2
4
3
4
4
5
1
5
2
5
3
5
4
6
1
6
2
6
3
6
4
Y
1,15
1,45
1,52
1,77
1,35
1,71
2,1
2,39
2,95
3,26
3,48
3,72
3,56
3,93
4,11
4,36
3,5
3,69
3,76
4,06
4,29
4,59
4,93
5,26
X
5,37
6,04
6,38
6,93
6,55
6,7
7,4
7,83
8,07
8,48
8,67
9,14
8,64
8,94
9,23
9,53
8,7
9,01
9,05
9,21
9,38
9,65
10,21
10,34
Y
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
3,20
1,85E-17
0,8884514
Scarti
impresa
X
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
8,31
Y
-2,05
-1,75
-1,68
-1,43
-1,85
-1,49
-1,10
-0,81
-0,25
0,06
0,28
0,52
0,36
0,73
0,91
1,16
0,30
0,49
0,56
0,86
1,09
1,39
1,73
2,06
X
-2,94
-2,27
-1,93
-1,38
-1,76
-1,61
-0,91
-0,48
-0,24
0,17
0,36
0,83
0,33
0,63
0,92
1,22
0,39
0,70
0,74
0,90
1,07
1,34
1,90
2,03
RSS within=
Resid
ui
Residui^2
0,56
0,31
0,26
0,07
0,03
0,00
-0,21
0,04
-0,29
0,08
-0,06
0,00
-0,29
0,09
-0,39
0,15
-0,04
0,00
-0,09
0,01
-0,04
0,00
-0,22
0,05
0,06
0,00
0,17
0,03
0,09
0,01
0,07
0,01
-0,05
0,00
-0,14
0,02
-0,10
0,01
0,06
0,00
0,14
0,02
0,20
0,04
0,04
0,00
0,25
0,06
1,013
Definiamo 3 stime corrette di RSS secondo tre ipotesi di modello
Dw  S1  0,266
Db  DT  Dw  S 2  0,747
DT  S 3  1,013
Dev. within
Dev. «spiegata» - between
Dev. Totale
avendo
N 6
T 4
K 2
Divise per gli opportuni gradi di libertà si otterranno tre stime della Varianza:
Vw = Varianza within
Vb = Varianza beetwen
Vt = Varianza totale
Rapportando le Varianze (test F), possiamo «testare» 3 ipotesi :
H 3 : 1   2  ....   6
1   2  ....   6
H1 : 1   2  ....   6
H 4 : 1   2  ....   6
datoH1 : 1   2  ....   6
I test (F)
F3 
S 3  S1 /N  1K  1  1,12(0,472)
S1 /  NT  N K  1
H 3 : 1   2  ....   6
1   2  ....   6
F1 
S 2  S1 /N  1K   1,08(0,479)
S1 /  NT  N K  1
H1 : 1   2  ....   6
F4 
S 3  S 2 /N  1  1,13(0,381)
S 2 /  N (T  1)  K 
H 4 : 1   2  ....   6
datoH1 : 1   2  ....   6
Il TEST dice che né le PENDENZE né le intercette sono
significativamente diverse
Costi e produzione (log per anno)
6
5
4
impresa 1
ln(costi)
impresa 2
impresa 3
3
impresa 4
impresa 5
impresa 6
2
1
0
5
6
7
8
ln(produzione)
9
10
11
S1
S2
S3
0,266126693
N=
6
0,746846584
T=
4
1,012973278
K=
2
NUM
GDLNUM DEN
GDLDEN
F3 0,746846584
15 0,266126693
6
F1 0,480719891
10 0,266126693
6
F4 0,266126693
5 0,746846584
16
VALORE
Signif.
1,122542914 0,474252428
1,08381437 0,482236631
1,140268211 0,379585972
Stima intercette variabili – Effetti fissi
Matrici:
Y
costi
1,15
1,45
1,52
1,77
1,35
1,71
2,10
2,39
2,95
3,26
3,48
3,72
3,56
3,93
4,11
4,36
3,50
3,69
3,76
4,06
4,29
4,59
4,93
5,26
matrice
X
dummy 1 dummy 2 dummy 3 dummy 4 dummy 5 dummy 6 prod
1
0
0
0
0
0
5,37
1
0
0
0
0
0
6,04
1
0
0
0
0
0
6,38
1
0
0
0
0
0
6,93
0
1
0
0
0
0
6,55
0
1
0
0
0
0
6,70
0
1
0
0
0
0
7,40
0
1
0
0
0
0
7,83
0
0
1
0
0
0
8,07
0
0
1
0
0
0
8,48
0
0
1
0
0
0
8,67
0
0
1
0
0
0
9,14
0
0
0
1
0
0
8,64
0
0
0
1
0
0
8,94
0
0
0
1
0
0
9,23
0
0
0
1
0
0
9,53
0
0
0
0
1
0
8,70
0
0
0
0
1
0
9,01
0
0
0
0
1
0
9,05
0
0
0
0
1
0
9,21
0
0
0
0
0
1
9,38
0
0
0
0
0
1
9,65
0
0
0
0
0
1
10,21
0
0
0
0
0
1
10,34
x'x
4
0
0
0
0
0
24,71
0
4
0
0
0
0
28,47
0
0
4
0
0
0
34,35
0
0
0
4
0
0
36,34
0
0
0
0
4
0
35,97
0
0
0
0
0
4
39,58
24,71 28,47 34,35 36,34 35,97 39,58 1699,72
x'y
5,89
7,55
13,40
15,96
15,01
19,07
676,78
(x'x)-1x'Y
-2,694
-2,912
-2,440
-2,134
-2,311
-1,904
0,674
x'x-1
9,43
10,58
12,77
13,50
13,37
14,71
-1,49
10,58
12,44
14,71
15,56
15,40
16,94
-1,71
a1
a2
a3
a4
a5
a6
beta
12,77
14,71
17,99
18,77
18,58
20,44
-2,07
13,50
15,56
18,77
20,10
19,65
21,62
-2,19
13,37
15,40
18,58
19,65
19,71
21,41
-2,16
14,71
16,94
20,44
21,62
21,41
23,80
-2,38
-1,49
-1,71
-2,07
-2,19
-2,16
-2,38
0,24
DIAGNOSTICA:
impresa Tempo Costi Costi
residuo
(i)
(t) osservati stimati
Ai
beta prod residuo ^2
1
1
1,149 0,925 -2,694 0,674 5,366 0,224 0,050
1
2
1,452 1,378 -2,694 0,674 6,038 0,074 0,006
1
3
1,523 1,606 -2,694 0,674 6,377 -0,084 0,007
1
4
1,766 1,981 -2,694 0,674 6,932 -0,215 0,046
2
1
1,350 1,502 -2,912 0,674 6,545 -0,151 0,023
2
2
1,711 1,605 -2,912 0,674 6,698 0,106 0,011
2
3
2,095 2,080 -2,912 0,674 7,402 0,016 0,000
2
4
2,395 2,365 -2,912 0,674 7,826 0,029 0,001
3
1
2,946 3,003 -2,440 0,674 8,072 -0,056 0,003
3
2
3,260 3,276 -2,440 0,674 8,477 -0,016 0,000
3
3
3,480 3,406 -2,440 0,674 8,669 0,074 0,005
3
4
3,718 3,720 -2,440 0,674 9,135 -0,002 0,000
4
1
3,562 3,693 -2,134 0,674 8,643 -0,131 0,017
4
2
3,934 3,892 -2,134 0,674 8,937 0,042 0,002
4
3
4,112 4,090 -2,134 0,674 9,231 0,022 0,000
4
4
4,355 4,288 -2,134 0,674 9,525 0,067 0,004
5
1
3,501 3,555 -2,311 0,674 8,700 -0,054 0,003
5
2
3,690 3,767 -2,311 0,674 9,015 -0,078 0,006
5
3
3,764 3,789 -2,311 0,674 9,046 -0,025 0,001
5
4
4,056 3,900 -2,311 0,674 9,211 0,156 0,024
6
1
4,291 4,418 -1,904 0,674 9,376 -0,127 0,016
6
2
4,594 4,605 -1,904 0,674 9,652 -0,011 0,000
6
3
4,934 4,982 -1,904 0,674 10,212 -0,048 0,002
6
4
5,255 5,069 -1,904 0,674 10,340 0,186 0,035
RSS=
gdl= NT-N-K
S^2
0,2640619
17
0,0155331
Lo SQM dei coefficienti è la radice della diagonale di S^2 (X’X)-1
Matrice di var-covar dei coefficienti
0,147
0,164
0,198
0,210
0,208
0,228
-0,023
0,164
0,193
0,228
0,242
0,239
0,263
-0,027
SQM dei coefficienti
a1
a2
a3
a4
a5
a6
beta
0,383
0,440
0,529
0,559
0,553
0,608
0,061
0,198
0,228
0,280
0,292
0,289
0,318
-0,032
0,210
0,242
0,292
0,312
0,305
0,336
-0,034
0,208
0,239
0,289
0,305
0,306
0,333
-0,034
0,228
0,263
0,318
0,336
0,333
0,370
-0,037
-0,023
-0,027
-0,032
-0,034
-0,034
-0,037
0,004
Calcolo di R2 per il modello con intercette variabili:

R 2  1   ei2 /  yi2  N y 2

R 2  1  0,2640 / 280,94  246,34  0,992375
Per il modello con unica intercetta:
R 2   2Txx / Tyy
R 2  (0,888) 2 42,633 / 34,632  0,970686
TEST PER LA SIGNIFICATIVITA’ DELLE INTERCETTE
USUALE test t:
a1
a2
a3
a4
a5
a6
beta
coeff.
-2,694
-2,912
-2,440
-2,134
-2,311
-1,904
0,674
sqm
0,383
0,440
0,529
0,559
0,553
0,608
0,061
test t
-7,037
-6,624
-4,615
-3,820
-4,177
-3,130
11,030
IL TEST DICE CHE LE INTERCETTE SONO SIGNIFICATIVAMENTE
DIVERSE DA 0
MA E’ PIU’ APPROPRIATO VALUTARE SE TUTTE LE INTERCETTE
SONO DIVERSE DA UN QUALCHE VALORE FISSATO (INTERCETTA
COMUNE)
VALUTIAMO L’INCREMENTO DI VARIANZA SPIEGATA TRA IL
MODELLO CON UNICA INTERCETTA (r) E QUELLO NON RISTRETTO
(6 INTERCETTE)
F( N 1, NT  N  K ) 
F(5,17)
( Ru2  R p2 ) /( N  1)
(1  Ru2 ) /( NT  N  K )
(0,9924  0,9707) / 5

 9,708 (0,00016)
(1  0,9924) / 17
L’INCREMENTO DI SPIEGAZIONE E’ SIGNIFICATIVO
INFATTI i.v. PREVEDE “MEGLIO”
valori previsti e osservati
6,000
5,000
4,000
3,000
2,000
1,000
0,000
5,000
6,000
7,000
Costi osservati
8,000
stime I.V.
9,000
stime Pooled
10,000
11,000
INSERIAMO UN EFFETTO VARIABILE NEL TEMPO E COSTANTE TRA GLI INDIVIDUI:
La matrice X si modifica così (vanno inseriti T-1 effetti tempo per evitare perfetta col linearità e quin
i coeff vanno letti come contrasti rispetti a t=1)
yit   i   t  xit   it
E
impr. 1 impr. 2 impr. 3 impr. 4
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
impr. 5
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
impr. 6 anno 2 anno 3 anno 4
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
1
prod
5,37
6,04
6,38
6,93
6,55
6,70
7,40
7,83
8,07
8,48
8,67
9,14
8,64
8,94
9,23
9,53
8,70
9,01
9,05
9,21
9,38
9,65
10,21
10,34
COEFF
-0,035
0,197
1,374
1,917
1,696
2,536
0,238
0,380
0,587
0,195
RSS=
gdl= NT-N-K
S^2
a1
a2
a3
a4
a5
a6
t2
t3
t4
beta
0,12248064
17
0,00720474
VAR/COVAR COEFFICIENTI
0,458
0,532
0,650
0,690
0,683
0,755
0,027
0,056
0,083
-0,081
0,532
0,622
0,758
0,804
0,796
0,881
0,032
0,065
0,097
-0,094
0,650
0,758
0,928
0,984
0,973
1,077
0,039
0,080
0,119
-0,115
0,690
0,804
0,984
1,046
1,033
1,143
0,042
0,085
0,126
-0,122
0,683
0,796
0,973
1,033
1,024
1,131
0,041
0,084
0,125
-0,121
0,755
0,881
1,077
1,143
1,131
1,253
0,046
0,093
0,138
-0,133
0,027
0,032
0,039
0,042
0,041
0,046
0,004
0,005
0,006
-0,005
0,056
0,065
0,080
0,085
0,084
0,093
0,005
0,010
0,012
-0,010
0,083
0,097
0,119
0,126
0,125
0,138
0,006
0,012
0,018
-0,015
-0,081
-0,094
-0,115
-0,122
-0,121
-0,133
-0,005
-0,010
-0,015
0,014
E quindi...
a1
a2
a3
a4
a5
a6
t2
t3
t4
beta
coeff.
-0,035
0,197
1,374
1,917
1,696
2,536
0,238
0,380
0,587
0,195
sqm
0,677
0,788
0,964
1,023
1,012
1,119
0,065
0,097
0,134
0,119
test t
-0,051
0,250
1,425
1,874
1,677
2,266
3,683
3,899
4,381
1,635
R2= 0,996463
Migliore del precedente??? In generale SI’
valori assoluti dei residui
0,6
0,5
0,4
residuo ti
0,3
residuo ai
0,2
residuo pooled
0,1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
-0,1
osse r v a z i oni ( i , t )
15
16
17
18
19
20
21
22
23
24
Ma se volessi stimare i valori medi….
Per impresa
Residui calcolati sui valori m edi per im presa
0,2
0,15
0,1
0,05
residui
0
1
2
3
4
-0,05
5
6
residuo ti
residuo ai
residuo pooled
-0,1
-0,15
-0,2
-0,25
-0,3
im presa
TOGLIENDO IL “POOLED”
zoom sui Residui calcolati sui valori m edi per im presa
5E-12
0
1
2
3
4
5
6
residui
-5E-12
residuo ti
residuo ai
-1E-11
-1,5E-11
-2E-11
im presa
I TEMPI FANNO PEGGIORARE LA STIMA
Valori medi per anno…….
valori assoluti residui
0,08
0,06
0,04
residui
0,02
residuo ti
0
1
2
3
-0,02
4
residuo ai
residuo pooled
-0,04
-0,06
-0,08
-0,1
anni
QUI, OVVIAMENTE, SONO LE INTERCETTE VARIABILI CHE PREVEDONO PEGGIO