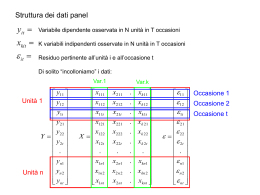
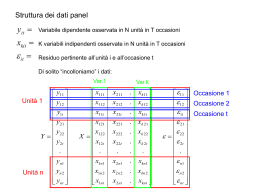
MODELLI A COMPONENTI DI VARIANZA
EFFETTI CASUALI - RANDOM EFFECTS
Le intercette individuali sono trattate come componenti stocastiche,
non come parametri fissi
Vi sono numerose considerazioni che rendono plausibile questa ipotesi:
1. Si tratta di caratteristiche non spiegate relative al singolo
individuo, è “naturale” ipotizzare distribuzioni probabilistiche (come
per la statura)
2. E’ difficile immaginare indipendenza tra le intercette e le
esplicative, ad esempio se stimiamo funzioni di produzione, le
intercette rappresenterebbero una sorta di capacità
imprenditoriale “tipica” dell’impresa e sicuramente questa ha
effetto sulla quantità di input utilizzati
3. Trattate come determinazione empirica di una variabile stocastica
comune a tutti gli individui, le intercette assumono un significato
riferibile all’intero collettivo e non al singolo soggetto
IL MODELLO
yit  xit  i  uit
Dobbiamo precisare la natura stocastica degli :
E ( i )  0
E (ui )  0
E ( i ,  j )   2
E ( i ,  j )  0
E (uit , u js )   u2
i j
i j
i  j ,t  s
E (uit , u js )  0
altrimenti
E ( i , u jt )  0
i, j , t
In sostanza è come se avessimo definito una scomposizione
dell’”usuale” residuo di regressione:
 it  i  uit
Quindi la varianza avrà 2 componenti e la presenza degli i
determina correlazione tra i residui di uno stesso individuo
Infatti si avrà PER LO STESSO INDIVIDUO:
Cov( it ,  is )   2   u2
Cov( it ,  is )   2
ts
ts
E per INDIVIDUI DIVERSI:
Cov( it ,  js )  0
i, t , s
I residui sono correlati, dobbiamo usare GLS
 è una matrice NTxNT diagonale a blocchi, con un blocco di dimensioni TXT in
corrispondenza di ciascun individuo:
1 0
0 
2

 .
.

0
0
 2   u2

2


i  
 .

2



0 
. 0 
. . 

. N 
.
.
 2
 2   u2 .
.
 2
 2
 2




.
.
2
2
.     u 
Dobbiamo trovare una stima per
 2 e  u2
Se “mediamo” il modello in T:
yit  xit   i  uit  yi  xi   i  ui
ma
ui  0
E quindi possiamo stimare i
La procedura di stima è la seguente:
1. Si stima il modello sulle medie individuali
2. Si calcolano i residui
3. Si mediano i residui per ciascun individuo
4. Si calcola la varianza “mediando” le varianze dei residui per
ciascun individuo
5. Si calcola la varianza complessiva (tutti gli individui)
6. Per differenza si trova
 u2
( 2 )
( 2   u2 )
yi  bxi   i  bxi   i  (ui  0)

2
E   it   it    (T  1) 2
 t

ˆ2 (i ) 
2





 it i
t
T 1
Ma b va stimato e quindi vanno corretti i gradi di libertà per la stima LSDV (k variabili)
s2 (i ) 
2





 it i
t
T  K 1
abbiamo N stimatori
 media
   it   i 2    it   i 2
 t

1
2
i
t
s   

N i  T  K  1  NT  NK  N


Se ora consideriamo gli scarti di tutti gli individui/tempi cioè tutti i residui della
regressione LSDV, abbiamo visto che
E ( i ,  i )   2   u2
Divisi per gli opportuni gradi di lbertà possono essere stimati come
eit2
s  
i
t N K
2
*
2





 it i
s2
eit2
1 i t
 s  s   

T
T NT  NK  N
i
t N K
2
u
2
*
In sostanza si calcolano la media delle varianza ENTRO e quella TOTALE
La differenza tra le due misura la componente di varianza non spiegata dalle
differenze individuali
Questo schema suggerisce anche un possibile test
Moltiplicatori di Lagrange, Breusch-Pagan
H 0 :  u2  0
H 1 :  u2  0
 
 Te

i

NT  
i
LM 
 1

2
2T  1   eit

 i t

2
χ² con 1 gdl
2
Effetti Fissi o casuali??
Il punto cruciale è: gli effetti individuali sono incorrelati con le esplicative?
Se così non è, abbiamo un problema di variabile omessa
Test di Hausman:
H 0 : Cov( i , X i )  0  ˆGLS  ˆOLS
H1 : Cov( i , X i )  0
test

 
   
W  ˆOLS  ˆGLS  1 ˆOLS  ˆGLS
  Var ˆ
 Var ˆ
OLS
è  2 (K )
GLS

Stimatore "Random Effects"
60
50
y
40
30
Y= 25,8+0,091 X
LM = 85
Hausmann = 97
pseudo-r = 0,81
20
10
0
0
2
4
6
8
10
x
12
14
16
18
Stimatore "random Effects - residui"
25
20
15
10
y
5
0
0
2
4
6
8
10
-5
-10
-15
-20
-25
x
12
14
16
18
I coefficienti della X
Overall
3.4974
Within
0.7691
Between
4.1195
LSDV
0.7691
Random E 0.9064