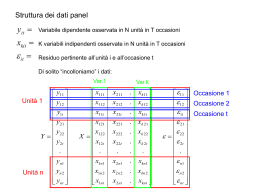
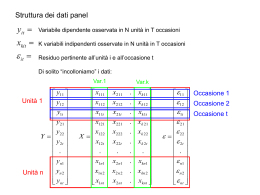
MODELLI A COMPONENTI DI VARIANZA
EFFETTI CASUALI - RANDOM EFFECTS
Le intercette individuali sono trattate come componenti stocastiche,
non come parametri fissi
Vi sono numerose considerazioni che rendono plausibile questa ipotesi:
1. Si tratta di caratteristiche non spiegate relative al singolo
individuo, è “naturale” ipotizzare distribuzioni probabilistiche (come
per la statura)
2. E’ difficile immaginare indipendenza tra le intercette e le
esplicative, ad esempio se stimiamo funzioni di produzione, le
intercette rappresenterebbero una sorta di capacità
imprenditoriale “tipica” dell’impresa e sicuramente questa ha
effetto sulla quantità di input utilizzati
3. Trattate come determinazione empirica di una variabile stocastica
comune a tutti gli individui, le intercette assumono un significato
riferibile all’intero collettivo e non al singolo soggetto
MODELLI A COMPONENTI DI VARIANZA
EFFETTI CASUALI - RANDOM EFFECTS
L’assunzione di intercette stocastiche ha, ovviamente, conseguenze
sulla struttura di Var/Covar del Modello e quindi sulla tecnica di
stima.
Come abbiamo visto in questi casi dobbiamo ricorrere (in prevalenza) a
GLS, o meglio a FGLS
Sintetizzando i passi che ci portano ad una stima FGLS:
1. Ipotizzare un modello della Var/Covar del fenomeno
2. (cioè) ipotizzare una “forma” per la matrice Ω
3.
4.
5.
6.
Ottenere una prima stima dei coefficienti e dei residui
Sulla base dei residui e delle ipotesi sulla forma stimare Ω
Utilizzando la stima di Ω ottenere una seconda stima dei residui
Ripetere i passi 4. e 5. fino a convergenza
MODELLI A COMPONENTI DI VARIANZA
EFFETTI CASUALI - RANDOM EFFECTS
Quindi otterremo tante strategie di stima quanti sono le ipotesi che
possiamo sensatamente formulare sull Var/Covar
Tali ipotesi saranno strettamente legate (cioè plausibili e coerenti)
almeno con il processo generatore dei dati che possiamo immaginare
per il fenomeno che ci interessa
Qui ne vedremo approfonditamente uno, e accenneremo ad altri,
tuttavia la logica della formulazione della strategia rimane la
stessa, cioè quella indicata in precedenza
Ogni ipotesi determina una strategia e questo spiega la pluralità di
stimatori che abbiamo a disposizione. Molto spesso questi stimatori
sono identificati con il nome del loro “ideatore”
IL MODELLO “Random effect” - BASE
Per la componente individuale si utilizzerà il simbolo  anziché  per chiarezza
yit  xit  i  uit
Questo è il modello “sostanziale”
Dobbiamo precisare la natura stocastica degli :
E ( i )  0
E (ui )  0
E ( i ,  j )   2
E ( i ,  j )  0
E (uit , u js )  
i j
Si ripete in t
i j
2
u
i  j ,t  s
E (uit , u js )  0
altrimenti
E ( i , u jt )  0
i, j , t
Questo è il modello di misura,
Da cui si desume la forma di Ω
In sostanza è come se avessimo definito una scomposizione
dell’”usuale” residuo di regressione:
 it  i  uit
Quindi la varianza avrà 2 componenti e la presenza degli i
determina correlazione tra i residui di uno stesso individuo
Infatti si avrà PER LO STESSO INDIVIDUO:
Cov( it ,  is )   2   u2
Cov( it ,  is )   2
ts
ts
E per INDIVIDUI DIVERSI:
Cov( it ,  js )  0
i, t , s
I residui sono correlati, dobbiamo usare GLS
 è una matrice NTxNT diagonale a blocchi, con un blocco di dimensioni TxT in
corrispondenza di ciascun individuo:
1 0
0 
2

 .
.

0
0
 2   u2

2


i  
 .

2



0 
. 0 
. . 

. N 
.
.
 2
 2   u2 .
.
 2
 2
 2




.
.
2
2
.     u 
Dobbiamo trovare una stima per
 2 e  u2
Se “mediamo” il modello in T:
yit  xit   i  uit  yi  xi   i  ui
ma
ui  0
E quindi possiamo stimare i
La procedura di stima è la seguente:
1. Si stima il modello sulle medie individuali
2. Si calcolano i residui
3. Si mediano i residui per ciascun individuo
4. Si calcola la varianza “mediando” le varianze dei residui per
ciascun individuo
5. Si calcola la varianza complessiva (tutti gli individui)
6. Per differenza si trova
 u2
( 2 )
( 2   u2 )
yi  bxi   i  bxi   i  (ui  0)

2
E   it   it    (T  1) 2
 t

ˆ2 (i ) 
2





 it i
t
T 1
Ma b va stimato e quindi vanno corretti i gradi di libertà per la stima LSDV (k variabili)
s2 (i ) 
2





 it i
t
T  K 1
abbiamo N stimatori
 media
   it   i 2    it   i 2
 t

1
2
i
t
s   

N i  T  K  1  NT  NK  N


Se ora consideriamo gli scarti di tutti gli individui/tempi cioè tutti i residui della
regressione LSDV, abbiamo visto che
E ( i ,  i )   2   u2
Divisi per gli opportuni gradi di lbertà possono essere stimati come
eit2
s  
i
t N K
2
*
2





 it i
s2
eit2
1 i t
 s  s   

T
T NT  NK  N
i
t N K
2
u
2
*
In sostanza si calcolano la media delle varianza ENTRO e quella TOTALE
La differenza tra le due misura la componente di varianza non spiegata dalle
differenze individuali
Questo schema suggerisce anche un possibile test
Moltiplicatori di Lagrange, Breusch-Pagan
H 0 :  u2  0
H 1 :  u2  0
 
 Te

i

NT  
i
LM 
 1

2
2T  1   eit

 i t

2
χ² con 1 gdl
2
Effetti Fissi o casuali??
Il punto cruciale è: gli effetti individuali sono incorrelati con le esplicative?
Se così non è, abbiamo un problema di variabile omessa
Test di Hausman:
H 0 : Cov( i , X i )  0  ˆGLS  ˆOLS
H1 : Cov( i , X i )  0
test

 
   
W  ˆOLS  ˆGLS  1 ˆOLS  ˆGLS
  Var ˆ
 Var ˆ
OLS
è  2 (K )
GLS

Stimatore "Random Effects"
60
50
y
40
30
Y= 25,8+0,091 X
LM = 85
Hausmann = 97
pseudo-r = 0,81
20
10
0
0
2
4
6
8
10
x
12
14
16
18
Stimatore "random Effects - residui"
25
20
15
10
y
5
0
0
2
4
6
8
10
-5
-10
-15
-20
-25
x
12
14
16
18
I coefficienti della X
Overall
3.4974
Within
0.7691
Between
4.1195
LSDV
0.7691
Random E 0.9064
Estensioni dei modelli per Dati Panel: 0.1 Panel bilanciati e NON
Finora abbiamo ipotizzato che ogni individuo i fosse asservato T volte.
Naturalmente nei casi concreti questo non sempre accade.
In simboli un individuo può esserere Ti volte quindi la numerosità complessiva
delle osservazioni non è più NxT ma diventa
N
t
i 1
i
In generale questo non modifica le procedure già viste, basterà nelle formule
tener conto che sono previsti Ti occasioni e apportare le modifiche necessarie.
(in alcuni casi le cose diventano lievemente più complicate (ad. Es. nelle
sommatorie non si può “raccogliere” T).
Alcune situazioni fanno eccezione come il test di Breusch-Pagan che prevede
una versione “apposita” per panel NON bilanciati.
Estensioni dei modelli per Dati Panel: 0.1 Time invariant Variables
Per le variabili che non variano tra le occasioni (es:sesso, anno di nascita,
residenza etc..) NON è naturalmente possibile stimare coefficienti separati dagli
effetti individuali (siano essi fissi o random).
Infatti, ad es. in LSDV i valori sulle colonne della matrice X che sono timeinvariant sono semplicemente multipli delle dummy individuali perché sono fissi
nel tempo per ciascun individuo.
Quindi le intercette individuali riassumono anche parte degli effetti di variabili di
altro genere.
Diverse strategie sono state suggerite per ovviare a questo grave problema, non
sempre soddisfacenti: la più nota è
1. Stimare con LSDV le intercette individuali considerando solo le time variant X
2. Stimare una regressione tra le intercette e le time invariant
3. Utilizzare i residui di 2 come esplicative del modello (senza dummies
individuali) per ottenere una unica intercetta e coefficienti per le time invariant
Non senza problemi, tema di ricerca aperto
Estensioni dei modelli per Dati Panel: 1. Mundlak’s Approach
Abbiamo visto che le stime ad effetti fissi e random hanno alcuni limiti:
Fissi: moltiplicano i parametri da stimare (1 per ogni individuo, la cui stima si
basa su “poche” osservazioni)
Random: presuppone una assunzione piuttosto inverosimile cioè che
l’eterogeneità non osservabile sia incorrelata con i regressori
E[ i | xi ]  0
Diversi autori hanno suggerito formulazioni diverse per rilasciare questa ipotesi,
cioè immagina una “forma funzionale” per la correlazione:
E[i | xi ]   ' xi.
E[i | xi ]   ' xi.
Inserendo questa condizione nel modello originale otteniamo
yit   ' xit   i  uit
  ' xit   ' x i.  uit   i  E  i | xi. 
  ' xit   ' x i.  uit   i.
Se γ = 0 allora ho un “fixed effect model”, quanto più γ≠ 0 , tanto più avrò
preponderanza dei “random effect”. Testando la significatività di γ posso
decidere la minore o minore adeguatezza delle ipotesi Fixed vs. Random
E’ ancora un metodo “random effect” , infatti specifica una “forma” per la matrice
di Var/Covar, diversa da quella vista in precedenza coerente con il rilascio
dell’ipotesi inverosimile di incorrelazione tra regressori e residuo
Si Stima con FGLS
Di solito è vista come una sorta di compromesso tra fixed e random effects
Estensioni dei modelli per Dati Panel: 2.  variabili:
Se i  variano da individuo a individuo, il modello diventa:
yit   i ' xit  uit
con
i     i
“random effect” sui 
E uit | xit   0
V uit | xit    u2
E  i | xit   0
V ui | xit   
Matrive di Var/Covar dei 
Se supponiamo di avere sufficienti gradi di liberta per stimare
(inizialmente) i i cioè le intercette per ciascun individuo possiamo
riscrivere OGNI BLOCCO di equazioni del modello in questo modo:
yi   ' i xi  ui
  ' xi  (ui  xi i )

 ii  E ( yi   ' xi )( yi   ' xi )' | xi    2 I T  xi xi '
Quindi la Ω avrà n blocchi diagonali di dimensione TxT come quello specificato
qui sopra. Questo determina la stima “corretta”

ˆ  X '  1 X
 X '  Y   W ˆ
1
n
1
i 1
i
i
dove

n
1
Wi      2  X 'i X i 
 i 1
1
 
1

1
2
      X 'i X i 


1
La stima empirica dei coefficienti richiede la stima di Γ (matrice di Var/Covar
dei coefficienti individuali βi ) che viene ottenuta dal solito processo iterativo
FGLS

1 
ˆ ˆ ' n  ' 
G


i i
n  1  i
ˆ



 1
  nt  Vi
i

dove
i
i
n
1
Vi  ˆ i2  X i ' X i 
Naturalmente il modello a coefficiente unico è un caso “ristretto” di quello a
coefficienti individuali, quindi la differenza tra i due modelli può essere
testata nei modi usuali. In particolare la Statistica (dove b* è il coefficiente
unico):

 
C   ˆi  ˆ* 'Vi 1 ˆi  ˆ*
i

  2 (n  1)
Estensioni dei modelli per Dati Panel: Modelli con variabili ritardate:
Yit = yt-1 +xitβ + i + uit, con i + uit=vit
Problema: yt-1 è correlato con i  stime inconsistenti di B anche su u è iid
Violazione dell’esogenità. E(ut/yt+k) ≠0 * yt-1 è correlato con ut-1 etc..
Quindi i vit sono correlati tra gli individui
Il problema è che T è spesso troppo “ridotto” per chè valgano le proprietà
asintotiche ad es la consistenza che possono mitigare la endogentà (nei
metodi precedenti si faceva leva su N)
Ma qui il bias è di ordine 1/T; non 1/N come prime
Ci servono altri modelli oltre LSDV
La soluzione qui solo citata è il ricorso a Variabili strumentali (IV) z correlate
con X ma non con u.
Soluzioni IV GMM
metodo IV applicato a differenze prime
IV con strumenti interni, di fatto si utilizzano i ritardi della dipendente
(e delle altre covariate)
Trasformazione in DIFFERENZE PRIME + IV
Con lagged Y le differenze non mi risolvono tutti i problemi
Le proposte di stima più note sono:
Anderson Hsiao
Arellano Bond
Blundell Blond
http://people.stern.nyu.edu/wgreene/Lugano2013/Greene-Chapter-11.pdf