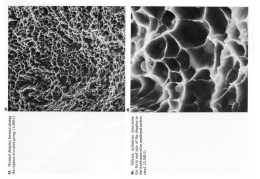
Proprietà meccaniche dei materiali Comportamento meccanico dei materiali: risposta alla sollecitazione di una forza esterna (trazione, compressione, taglio, costante o variabile nel tempo). Definiremo: •Resistenza: capacità di un materiale di resistere a trazione/compressione (elastica) •Duttilità: capacità di un materiale subire una deformazione plastica (permanente) prima della rottura. Opposta a fragilità •Tenacità:indica la capacità di assorbire energia di un materiale, spendendola nella sua deformazione. •Durezza: capacità di un materiale di resistere alla penetrazione di un altro materiale (incisione, graffi) La loro misura è effettuata tramite test standardizzati (es. American Society for Testing and Material o International Organization for Standardization) Materiali per l’ottica F A0 l l l l l 0 0 sforzo 0 Deformazione nominale F A 0 tg ( ) Sforzo e deformazione In un mezzo isotropo, il materiale si contrae/dilata nelle altre due direzioni a seguito della dilatazione/contrazione lungo l’asse di sollecitazione. La costante di proporzionalità è detta modulo di Poisson x y z z Si può facilmente dimostrare che la variazione di volume relativa del materiale in esame è data da V l 1 2 V l 0 0 Dunque =0.5 corrisponde ad un materiale completamente incomprimibile Materiali per l’ottica Sforzo e deformazione Legge di Hooke: Causa: sforzo/stress Effetto: deformazione E : dimensioni di una pressione unità di misura Pa (N/m2) : numero puro, può essere >0 (trazione) o <0 (compressione) E: modulo elastico o di Young espresso in GPa Gtg : dimensioni di una pressione unità di misura Pa (N/m2) G: modulo di taglio (shear) espresso in GPa Per materiali isotropi vale la relazione E 2G 1 Materiali per l’ottica Origine microscopica della costante elastica Condizione di equilibrio stabile r o r>ro, molla cerca di contrarsi r<ro, molla cerca di dilatarsi Le costanti elastiche macroscopiche dipendono dall’andamento delle forze inter-atomiche (approssimazione armonica del potenziale) Materiali per l’ottica Capacità di assorbire una deformazione plastica senza rompersi: alta=duttile (es. oro) bassa=fragile (es. vetro) E’ dipendente dalla temperatura:capacità di riposizionamento di difetti ed atomi (diffusione atomica) dipendono esponenzialmente dalla temperatura RESILIENZA = Capacita’ di assorbire energia deformazione Cap.10, 6,1 Sforzo e deformazione “duro” Materiale E (GPa) Poisson Diamante 1000 0.2 200 0.3 Oro 80 0.4 Vetro 70 0.2 PMMA 2 0.4 0.002 0.5 Acciaio “morbido” Caucciù Materiali per l’ottica Se a una barretta di dimensioni 5 cm x 1 cm2 applichiamo una forza a trazione pari a 1 kN osserviamo un allungamento pari a Diamante:500 nm (0.5 µm) Vetro: 7 µm Caucciù: 25 cm !!!!! Variazione percentuale di volume 0.6 10-5 per diamante e 0 per caucciu’ Cap.10, 6,1 Soda-lime glass for containers Properties Soda-lime glass for windows Chemical composition, wt% 74 SiO2, 13 Na2O, 10.5 CaO, 1.3 Al2O3, 0.3 K2O, 0.2 SO3, 0.2 MgO, 0.04 Fe2O3, 0.01 TiO2 73 SiO2, 14 Na2O, 9 CaO, 4 MgO, 0.15 Al2O3, 0.03 K2O, 0.02 TiO2, 0.1 Fe2O3 Viscosity log(η, dPa·s or Poise) = A + B / (T in °C − To) 550–1450°C: A = −2.309 B = 3922 To = 291 550–1450°C: A = −2.585 B = 4215 To = 263 Glass transition temperature, Tg, °C 573 564 Coefficient of thermal expansion, ppm/K, ~100-300°C 9 9.5 Density at 20°C, g/cm3 2.52 2.53 Refractive index nD at 20°C 1.518 1.520 Dispersion at 20°C, 104×(nF−nC) 86.7 87.7 Young's modulus at 20°C, GPa 72 74 Shear modulus at 20°C, GPa 29.8 29.8 Liquidus temperature, °C 1040 1000 Heat capacity at 20°C, J/(mol·K) 49 48 Surface tension, at ~1300°C, mJ/m2 315 Chemical durability, Hydrolytic class, after ISO 719[5] 3 3...4 Critical stress intensity factor,[6] (KIC), MPa.m0.5 ? 0.75 Il vetro: effetti composizionali sulle proprietà strutturali Materiali per l’ottica Cap. 13 Durezza vetri • Prove semplici e poco costose • Non distruttive • Altre proprieta’ possono essere dedotte dalla durezza Materiali per l’ottica PMMA Durezza Misura la resistenza di un materiale ad essere inciso (deformazione plastica) da un piccolo incisore/penetratore di materiale diverso. Si ha quindi una definizione di scale comparative o semiquantitative che dipendono dalla tecnica standard di misurazione (Mohs, Rockwell, Vickers..etc) 2 * peso HB D D D d 2 Materiali per l’ottica 2 HV 1.854 * peso d 2 i più larga l’impronta meno duro il materiale Proprietà a trazione: duttilità e fragilità Viene quantificato come la percentuale di allungamento alla quale si osserva la frattura su un campione standard (50 mm) A(l 50mm) 100 0 l l l F 0 0 Materiale Snervamento Carico (MPa) rottura (MPa) Duttilità (%) Acciaio 300 700 18 Oro 110 130 45 Vetro Si rompe prima 70 0 PMMA 45 55 4 Materiali per l’ottica Proprietà a trazione: la frattura Cosa avviene quando eccediamo il carico di rottura di un materiale? Il materiale si separa in due pezzi distinti: la frattura. Una prima fissura iniziale (cricca) si propaga al resto del materiale fino alla sua completa separazione in due parti. Questa può avvenire in due modi alternativi: Frattura duttile: il materiale si deforma plasticamente assorbendo una grande quantità di energia prima della rottura. Cricca che si propaga lentamente e che cessa il suo moto se il carico non viene aumentato. (p.e. filo d’oro) Frattura fragile: scarsa o nulla deformazione plastica prima della rottura, basso assorbimento di energia. Propagazione della cricca rapida e catastrofica, ovvero, prosegue senza aumentare il carico. (p.e. vetro) Materiali per l’ottica
Scaricare