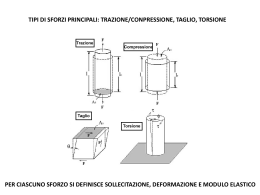
Proprietà meccaniche
• Il comportamento meccanico di un materiale rappresenta la risposta offerta nei confronti
di un carico applicato ovvero di una forza. Importanti proprietà meccaniche sono la
rigidezza, la resistenza, la duttilità , la tenacità, la durezza.
• Le proprietà meccaniche dei materiali vengono determinate mediante la realizzazione di
prove meccaniche che vengono eseguite mediante procedure normalizzate (ASTM-UNIISO)
• Il comportamento meccanico può essere determinato mediante delle prove di sforzodeformazione. In tali prove il carico è applicato staticamente e uniformemente sulla sezione
del componente.
Prova di trazione
• Il carico è applicato lungo l’asse del provino che è sagomato in modo tale che la
deformazione sia confinata nella zona centrale del provino, quella a sezione costante.
• La macchina di prova è capace di misurare il carico applicato mediante la cella di carico e
la deformazione mediante l’estensimetro simultaneamente.
• La prova di trazione è di tipo distruttivo ovvero il provino viene deformato in maniera
permanente e molto spesso fratturato.
Prova di trazione
sforzo nominale o ingegneristico

F
A0
deformazione nominale o ingegneristica

l  l0
l0
deformazione elastica = deformazione reversibile
  E
Legge di Hooke
E è detto modulo elastico o modulo di Young: esso è
una misura della rigidezza del materiale
Per la prova di taglio vale una analoga legge di
proporzionalità:
  G
G è detto modulo di taglio
Prova di trazione

y
x

z
z
  0.5 
rapporto o modulo di Poisson
V  V0
0
V0
Per un materiale isotropo ed elastico E, G e n sono legati tra loro dalla relazione:
E  2G1   
Prova di trazione
La deformazione plastica (snervamento) è una deformazione permanente e non
recuperabile. Dal punto di vista atomico la deformazione plastica corrisponde alla
rottura di alcuni legami tra atomi vicini allo scorrimento degli stessi ed alla
conseguente formazione di nuovi legami tra nuovi atomi vicini. Una volta rimosso lo
sforzo gli atomi e le molecole non possono ritornare nelle posizioni originali
Solido cristallino → scorrimento che coinvolge il moto delle dislocazioni
Solido amorfo → scorrimento viscoso
Prova di trazione
Limite di proporzionalità: il punto oltre il quale la curva sforzo-deformazione non
segue più l’andamento lineare (difficile da determinare).
Per convenzione il carico di snervamento è dato dalla ordinata del punto di
intersezione tra la curva - e una retta parallela al tratto elastico e passante per
una deformazione dello 0.002. Ovvero il carico di snervamento è quello in
corrispondenza del quale si ha una deformazione permanente dello 0.2%
Prova di trazione
La resistenza a rottura è lo sforzo rappresentato dal punto di massimo della curava di
sforzo-deformazione.
Le deformazioni che avvengono sul provino sino al punto M sono ripartite
uniformemente lungo tutta la sua lunghezza. Invece in corrispondenza del punto M si
comincia a formare un piccolo restringimento di sezione dove vengono localizzate tutte
le deformazioni successive. Questo fenomeno è detto strizione
Prova di trazione
La duttilità è una misura della deformazione plastica che il materiale può subire
senza rompersi. Un materiale che presenta scarsa o inesistente deformazione
plastica viene detto fragile.
Come misura della duttilità si può prendere l’allungamento percentuale a rottura o la
riduzione percentuale della sezione a rottura.
 l f l0 
  100
A%  
 l0 
 A0  Af
S%  
 A0

  100

Prova di trazione
La resilienza è la capacità di un materiale di assorbire energia se sottoposto a
deformazione elastica e poi di rilasciarla durante la fase di scarico. La grandezza
associata a questo fenomeno è il modulo di resilienza Ur che rappresenta l’energia di
deformazione per unità di volume necessaria per portare un materiale dallo stato
iniziale a raggiungere il suo limite di snervamento.
y
U r     d
0
  E
 y2  y2
Ur  E 
2 2E
I materiali resilienti sono quelli che hanno un
elevato limite di snervamento e un basso
modulo elastico
Prova di trazione
La tenacità è la capacità di un materiale di assorbire energia fino al raggiungimento
della rottura. Nel caso di condizioni statiche la tenacità può essere determinata dalla
curva - come l’area sottesa dalla curva stessa. Un materiale tenace presenta quindi
sia una elevata resistenza che una elevata duttilità.
Prova di trazione
Analizzando la curva s-e nominale si nota che dopo il raggiungimento del punto M la curva
comincia a decrescere come se il materiale si indebolisse. In realtà ciò non è vero dal
momento che lo sforzo cresce sempre al crescere della deformazione. Quello che invece
varia è la sezione del provino per effetto della strizione. Lo sforzo nominale è riferito alla
sezione iniziale del provino e quindi non può tenere in conto dell’effetto di strizione.
sforzo reale
F

Ai
li
deformazione reale
 
l0
l
dl
 ln i
l
l0
La regione di curva - compresa fra il tratto
dove inizia la deformazione plastica e il punto di
inizio della strizione può essere decritto dalla
seguente legge:
 R  K Rn
I valori di K ed n sono costanti che dipendono
dal tipo di materiale. n (esponente di
indurimento per deformazione plastica) < 1
In corrispondenza della strizione lo stato tensionale diventa triassiale. Lo sforzo realmente
agente in direzione assiale è quindi leggermente inferiore a quello calcolato basandosi sul
valore del carico applicato. Di qui la curva “corretta”.
Prova di trazione
Quando il carico viene rilasciato durante una prova di trazione una frazione della
deformazione (la parte elastica) viene recuperata. La curva di scarico è una linea retta
parallela al tratto elastico. Se il carico viene riapplicato le condizioni di snervamento
saranno nuovamente raggiunte in corrispondenza dello sforzo al quale era iniziato lo
scarico
Durezza
La durezza è la misura della resistenza offerta da un materiale alla deformazione plastica
(ovvero a un piccolo penetratore o incisore)
Scala di Mohs: scala empirica con valori tra 1 per il talco e 10 per il diamante, è
costruita considerando la capacità di un materiale di riuscire a penetrare un altro più
morbido
Oggi si utilizzano delle tecniche standard per la valutazione della durezza che
prevedono l’impiego di un penetratore il quale viene forzato a penetrare attraverso la
superficie del materiale da analizzare. La profondità e la forma dell’impronta viene poi
misurata e da queste misure si risale alla valutazione della durezza espressa con un
numero. Più è larga e profonda l’impronta minore è la durezza del materiale.
Le misure di durezza non sono valori assoluti ma relativi e sono legate al tipo di tecnica
impiegata: bisogna fare attenzione quando si paragonano valori ottenuti con
metodologie diverse !!!!
Le prove di durezza sono:
•Semplici e poco costose
•Non distruttive
•Da una prova di durezza si possono dedurre altre proprietà meccaniche come il carico di
rottura
Durezza: prova Rockwell
Penetratore: sfere di acciaio incrudito con diametri pari a 1/16, 1/8, ¼, ½ di pollice
oppure in un diamante a forma conica.
La durezza è misurata come la differenza di profondità delle impronte generate
dall’imposizione di un carico basso e poi da un carico maggiore. L’imposizione di un
carico basso serve a garantire una maggiore accuratezza dei risultati.
Carichi:
1.
Rockwell: Fmin=10Kg, Fmax=60,100,150 Kg
2.
Rockwell superficiale Fmin=3Kg, Fmax=15,30,45 Kg
In corrispondenza del carico e del tipo di penetratore utilizzato esistono diverse scale di
durezza contrassegnate da diverse lettere dell’alfabeto (A-K per la Rockwell e
N,T,W,X,Y per la Rockwell superficiale)
Quando si riportano i valori della durezza bisogna indicare sia il numero della
durezza che la scala impiegata; la scala si indica con HR seguita dal codice della
scala. Esempi: 80 HRB, 60 HR30W
Durezza: prova Rockwell
Per ogni scala la durezza può arrivare sino a 130, sono affidabili soltanto i valori
compresi tra 20 e 100. Se si ottiene un valore esterno a tale intervallo si passa ad
un’altra scala, tra le scale vi è un certo livello di sovrapposizione.
Lo spessore del provino deve essere pari ad almeno 10 volte la profondità dell’impronta,
mentre i centri di due diverse impronte devono essere separati da una distanza almeno
pari a 3 diametri dell’impronta.
Durezza: prova Brinell
Penetratore: sfere di acciaio incrudito o di carburo di tungsteno con diametro pari a 10
mm. I carichi sono compresi tra 500 e 3000 Kg e durante il test il carico viene
mantenuto costante per tempo compreso tra 10 e 30 secondi. Il numero di durezza
brinell HB è funzione sia del carico applicato che del diametro dell’impronta secondo
la relazione:
D
HB 
d
In questo caso c’è soltanto una scala !!
2P
D( D  D 2  d 2 )
2 * profondità dell’impronta
Prove di microdurezza: Vickers e Knoop
Penetratore:
Vickers: diamante a forma di piramide a base quadrata
Knoop: diamante a forma di piramide a base rettangolare
Carico: 1-1000 g
Le durezze Knoop e Vickers vengono designate rispettivamente dalle lettere HK e HV e
le loro scale sono praticamente equivalenti. Entrambi i metodi sono adatti per misurare
piccole aree o regioni specifiche
Durezza
Per quanto riguarda la conversione
dei valori di durezza ottenuti con
metodologie diverse allo stato attuale
non è stata ancora sviluppata una
procedura di conversione univoca. Le
metodologie di conversione attuali si
basano su raffronti sperimentali e
dipendono fortemente dal materiale in
esame. In figura è presentata una
tabella di conversione per gli acciai.
Durezza
Sia il carico di rottura che la durezza
sono indicatori della resistenza dei
materiali alla deformazione plastica.
Conseguentemente queste grandezze
possono
essere
considerate
approssimativamente proporzionali al
carico di rottura.
Per gli acciai vale:
TS = 3.45 x HB
Frattura
Formazione e propagazione della cricca
duttile: stabile
fragile: instabile
Transgranulare o intergranulare
Frattura

a
 m   0 1  2

 t



1/ 2



 a
m
Kt 
 2
0
 t



1/ 2
Fattore di concentrazione
degli sforzi
Resistenza a
rottura reale
circa 1/10-1/1000
di quella teorica
Frattura
Frattura: criterio di Griffith
L’energia elastica rilasciata durante la propagazione della cricca = energia necessaria
alla formazione di nuove superfici libere per effetto della propagazione stessa
(incremento dell’energia superficiale del sistema)
 2 E s 
c  


a


1/ 2
 2 E  s   p  

 c  
a


1/ 2
Gc  2 s   p   Gc 
 2 a
E
Velocità di rilascio dell’energia critica di
deformazione
Frattura
 ij 
K
f ij  
2r
K è detto fattore di intensificazione degli sforzi
K  Y a ,
a
Y  Y 
W 
Frattura
Tenacità a frattura
K Ic  Y c a ,
a
Y  Y 
W 
Condizione di deformazione piana
 K Ic 

B  2.5
 
 y 
2
Frattura per Fatica
Frattura per Fatica
Frattura per Fatica
Frattura per Fatica
Frattura per Fatica
Frattura per Fatica