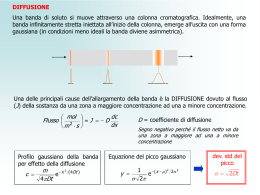
Equilibrio tra le fasi
Dc = C1/C2, dove C indica la somma della concentrazione
delle varie forme in cui può essere presente la sostanza che si
ripartisce tra le fasi.
Equilibrio
FASE 1
prima
dopo
0
V1
C1
V1
C0
V2
C2
V2
Concentrazione
Volume
FASE 2
Concentrazione
Volume
1
p = frazione di soluto nella fase 1 =
q = frazione di soluto nella fase 2 =
C0 V2 = C1 V1+ C2 V2
Dividendo per C2V2 numeratore e
denominatore si ha:
p=
q=
2
n=0
n=1
Le frazioni di soluto nei recipienti
dopo l’equilibrio sono i termini
individuali dell’espressione (q+p)n
n=2
Se indichiamo con (Fr,n) la
frazione di soluto contenuta in r
dopo n trasferimenti abbiamo:
n=3
n=4
r=0 r=1 r=2 r=3
3
È possibile dimostrare che, matematicamente
rmax
Il calcolo di F mediante l’espressione fattoriale diventa particolarmente lungo
quando n ed r diventano grandi.
Fortunatamente, in queste condizioni, la distribuzione binomiale può essere
approssimata ad una distribuzione normale (gaussiana) che ha la forma:
Per n>24
4
Separazione di due soluti (Dc1 =3, Dc2=1/3) per n=25 ed n=100
5
Lyman C. Craig (1906-1974)
A manual version of Lyman C. Craig's CCD machine
designed by Erich Hecker
6
TEORIA DEL PIATTO
relazione con la distribuzione in controcorrente
In cromatografia sia r che n sono
molto grandi, ma n>> r, per cui
Applicando l’approssimazione di Stirling
7
La frazione di ogni soluto sarà distribuita entro un certo numero di recipienti (piatti
teorici) specificato dalla precedente equazione.
Se vogliamo calcolare la frazione di soluto per rmax (massimo del picco), ricordando
che rmax = np si ha
Consideriamo la situazione in cui il soluto costituito da m moli totali, e la sua
massima concentrazione si trovi in rmax = N, avremo che la quantità totale Q
nel recipiente rmax = N sarà
8
Il soluto si muove lungo la colonna di N piatti in un tempo =tR (tempo
impiegato dal massimo della concentrazione ad uscire dalla colonna), per cui
la velocità di uscita espressa come piatti/tempo sarà N/tR e la velocità della
massima quantità Smax sarà
9
La quantità m è proporzionale all’area del picco, mentre la velocità
del massimo di concentrazione di uscita (massimo del picco) è
proporzionale alla sua altezza. considerando in prima
approssimazione il picco triangolare ed esprimendo l’altezza in unità
arbitrarie e la base in unità di tempo avremo
e considerando il picco
gaussiano (tw = 4τ), dove τ è la
deviazione standard espressa
in unità di tempo
10
Piatti teorici
• Per descrivere il processo cromatografico è utilizzata una similitudine
derivante dalla teoria della distillazione. Il sistema cromatografico è
immaginato simile ad una colonna di distillazione, cioè composta da una
serie di strati sottili chiamati piatti teorici; in ognuno di questi
microelementi della colonna si realizza l’equilibrio di distribuzione del
soluto tra fase stazionaria e fase mobile. Lo spostamento del soluto lungo
la colonna è dovuto all’azione dinamica della fase mobile
I termini numero di piatti
teorici (N) e altezza del
piatto
(HETP,
Height
Equivalent
to
Theoric
Plate) sono comunemente
utilizzati in cromatografia
per
quantificare
le
prestazioni dei sistemi
cromatografici
11
1)
2)
Altezza equivalente di piatto teorico H
Numero di piatti teorici N
N
L = lunghezza colonna
L
H
Piatto teorico: sezione della colonna che consente di realizzare un equilibrio reversibile
di ripartizione di un componente fra le fasi. Poiché in cromatografia si ha una sequenza
continua di stati di equilibrio e non vi è possibilità di realizzare una singola separazione,
N ha un significato puramente matematico.
Più elevato è il numero di piatti teorici, più grande è la probabilità di una separazione
(migliore è la capacità di separazione della colonna). N è proporzionale alla lunghezza
della colonna.
t 
N  R 
 
2
t 
N  16 R 
W
2
W
L’altezza equivalente al piatto teorico (H = L/N) consente di confrontare l’efficienza di
colonne di differente lunghezza.
12
w½= 2.35σ
LIMITI DELLA TEORIA DEL PIATTO
• K è costante ed indipendente dalla
concentrazione del soluto
• L’equilibrio è rapido rispetto alla velocità della
fase mobile
• Non c’è diffusione longitudinale del soluto
(recipienti con pareti)
• La fase mobile è aggiunta per incrementi e
non in continuo.
14
DI queste assunzioni solo la prima è valida nella
cromatografia analitica ed è mantenuta nella teoria
dinamica che risulta anche essa valida solo per la
cromatografia con isoterma di ripartizione lineare
I piatti nella colonna non esistono, sono una
approssimazione e non una realtà fisica, l’equilibrio non è
istantaneo e la diffusione avviene lungo tutta la colonna,
mentre il passaggio da una fase all’altra avviene prima
che l’equilibrio sia stabilito.
Infine, la larghezza del picco dipende dalla velocità con
cui la fase mobile fluisce lungo la colonna.
15
Le molecole di un analita non si muovono lungo la colonna con la stessa velocità: la loro
dispersione ha generalmente un profilo Gaussiano. Il centro del profilo (banda di
eluizione)
rappresenta
la
velocità
media.
I fattori che provocano deviazioni dal valore medio sono:
1.
diffusione longitudinale (diffusione delle molecole dalla zona
a maggiore concentrazione a quella a minore in direzione
parallela all’asse della colonna);
2.
percorsi multipli;
3.
trasferimento di massa tra fase
mobile e fase stazionaria.
16
17
18
LA TRATTAZIONE FISICA DI
QUESTI FENOMENI HA DATO
ORIGINE ALLA
TEORIA
DINAMICA
19
TEORIA DINAMICA
σ2 = Σσj2
H = ΣHj
Diffusione longitudinale
σmd = (2γm Dm t)½
Ricordando che *
N = tr2/σt2 = L2/ σL2 ; H = L/N = σL2/L e t/L =1/u
Hmd = 2γm Dm /u ; Hsd = 2k’γs Ds /u
Dove γ è il fattore di ostruzione, D il coefficiente di
interdiffusione e u la velocità lineare
20
MOLTEPLICITA DEI CAMMINI
Detta anche “eddy diffusion”
Hfed = 2 λ dp
• λ è una misura della non
eguaglianza dei flussi
vale solo per le colonne
impaccate
21
TRASFERIMENTO DI MASSA
Colonne impaccate
Nella fase mobile
Hmfd = ω dp2 u/Dm
ω = fattore di impaccamento
dp = diametro delle particelle
Nella fase stazionaria Hsfd = 2/3(2k’/[1+k’]2) (df2/Ds) u
df = spessore del film di fase stazionaria
Colonne tubolari
Nella fase mobile Hmfd = (1+6k’+11k’2)dt2u/96(1+k’)2Dm
dt = diametro del tubo
Nella fase stazionaria
22
la formula è come per le impaccate
24
Equazione di Van Deemter
L’equazione che meglio riproduce i dati sperimentali è
la combinazione di tre equazioni che esprimono i
tre fenomeni diffusivi
H = A + B/u + Cmu + Cs u
25
L’equazione di Giddings modifica
l’equazione di Van Deemter
Sources of Extra Column Dispersion
29
Risoluzione cromatografica
La possibilità di separare due
o più sostanze è descritta dal
parametro detto risoluzione,
che misura la capacità di un
sistema cromatografico di
separare due analiti con
caratteristiche simili:
R
2( tR )B  ( t R )A 
2Z

WA  WB
WA  WB
Se la risoluzione non è
sufficiente (R < 1), i due
picchi non possono essere
quantificati
in
maniera
corretta
30
1
   1  k IB
R
N
 I
4


 kB  1
Effetto della selettività, dell’efficienza e del fattore di capacità sulla risoluzione
risoluzione scarsa
picchi non separati
buona risoluzione dovuta a
buona efficienza
picchi stretti
buona risoluzione dovuta a
buona selettività
picchi distanti
risoluzione scarsa dovuta ad
un basso fattore di capacità
31
Risoluzione e separazione
Capacità di picco
35
36
ELUIZIONE IN GRADIENTE
37
38
39
40