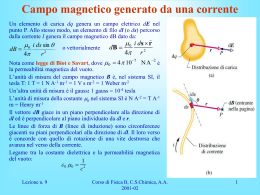
In natura esistono dei materiali, detti magneti, che hanno la
capacità di attrarre pezzetti di ferro (ed anche pezzetti di altro
metallo come il nichel, il cobalto, cromo oltre che composti e leghe
dei suddetti metalli). Già dal seicento a.C. era nota l’esistenza di un
minerale di ferro capace di attrarre a sé dei pezzettini di ferro. Oggi
sappiamo che questo minerale è ossido di ferro Fe3O4 detto
magnetite.
Dato un magnete indichiamo con N ed S i suoi due estremi.
Analogamente a quanto accade per le cariche elettriche si verifica
che accostando le estremità di due magneti questi si attraggono o si
respingono; si respingono se i poli sono dello stesso segno e si
attraggono se hanno poli opposti.
La differenza fondamentale dei magneti rispetto alle cariche
elettriche consiste nel fatto che, mentre è possibile isolare una
carica elettrica positiva o negativa, ciò non è possibile con i
magneti.
Se infatti prendiamo un magnete e lo spezziamo in due parti,
vediamo che ciascuna delle due parti costituisce un nuovo
magnete completo, in quanto nelle nuove facce creatasi si
generano poli di nome opposto a quelli preesistenti
N
N
S
S
N
S
esperienza della calamita spezzata
In analogia al campo elettrico, anche nel caso del campo
magnetico, vediamo che la zona intorno ad un magnete è sede di un
campo magnetico. Questo può essere visualizzato, attraverso della
limatura di ferro, mediante delle linee di forza.
Le linee si richiudono sempre su se stesse; dato che non è
possibile avere un polo isolato, non è possibile avere sorgenti
sorgenti o “pozzi” di linee di forza come nel campo elettrico.
L’analogo del vettore E è il vettore B così definito: è sempre tangente
alle linee di forza e di verso dato dal verso in cui punterebbe il nord
un ago magnetico, Per il modulo bisogna vedere caso per caso.
FORZA di LORENTZ
B
q
v
Consideriamo una
carica q positiva
lanciata con velocità
v in un campo
magnetico; essa è
sottoposta ad una
forza F
F  q  v B
Il modulo è:
F  qvB sin 

è l’angolo formato da
v
e
F
B
B
La direzione di F è perpendicolare sia a
B che a
v
v
Unità di misura e dimensioni fisiche di B
F
B
qv


 N   N 
 T 
 m  

Am

C
 
s 

Tesla
Per determinare il verso di F si può ricorrere alla regola della
mano destra:
B
v
F
Si dispone il pollice nel
verso della velocità della
carica (supposta positiva),
le dita nel verso di B; il
verso di F è perpendicolare
al palmo della mano e
uscente da esso.
Nel caso di carica negativa
occorre orientare il pollice in
verso opposto a v.
Se sono presenti sia un campo magnetico che un campo elettrico,
la forza agente sulla carica è quella risultante:
FR  qo E  q0 v B
Legge di Biot - Savart
Campo magnetico prodotto da un lungo (infinito)
filo rettilineo percorso da corrente elettrica.
i
B
d
Un filo rettilineo percorso da
corrente elettrica determina un
campo magnetico le cui linee
sono concentriche al filo.
0  i
B
2   d
d è la distanza del punto dal filo
 0 è la permeabilità
magnetica del mezzo
 0  4   10 7
Nel vuoto
T m
A
i
B
d
La direzione di B in un punto è
tangente alla traiettoria. Il verso si
trova con la regola della mano destra:
si dispone il pollice nel verso di i; le
dita piegate danno il verso di B.
Azione di un campo magnetico su un filo percorso da corrente
elettrica.
Dato un filo percorso da una corrente I, se si immerge il filo in un
campo magnetico B il filo è sottoposto ad una forza data da
F  I  l B
i

B
F  I  l  B  sin 
l è un vettore parallelo al filo, di modulo pari alla lunghezza del
filo e verso uguale a quello della corrente.
La direzione di F è perpendicolare al palmo della mano destra e il
verso è entrante
Se il filo è perpendicolare a B
F  I  l  sin 90
F  i l  B
l
i
B
Campo magnetico al centro di una spira conduttrice circolare
percorsa da corrente elettrica
Data una spira circolare di raggio r percorsa da corrente
elettrica I, l’intensità del campo magnetico è:
i
B
B è entrante
B
0  I
2r
1
r
La (1) si applica solo al centro
della spira.
La direzione di B è perpendicolare
al piano della spira in
corrispondenza del suo centro. Il
verso è dato dal pollice della mano
destra quando le dita sono piegate come la corrente.
Campo magnetico all’interno di un
solenoide percorso da corrente
Il solenoide è un filo elettrico costituito da spire uguali,
ravvicinate e parallele fra loro; è composto da N spire
Il vettore B è dato
da:
B
 o  N .I
l
N è il numero di spire
2 l è la lunghezza del
solenoide
La direzione di B è tangente alle linee d’induzione. Il verso si trova
con la regola della mano destra.
Si pone la mano destra sul solenoide in modo che la corrente circoli
dal polso alle dita; il pollice indica il verso del campo.
Se si pone
n
N
l
La (2) diventa
n è detta densità lineare e rappresenta il
numero di spire per unità di lunghezza
B  0  n  I