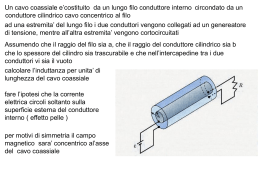
CORRENTI ELETTRICHE E CAMPI
MAGNETICI
•Forze magnetiche su una corrente elettrica;
•Forza magnetica su una corrente elettrica
rettilinea;
•Effetto Hall;
•Campo magnetico generato da una corrente,
legge di Ampere-Laplace;
•Forze magnetiche tra correnti
•Le unità di misura elettromagnetiche
FORZE MAGNETICHE SU
CORRENTI ELETTRICHE
La forza F su una carica q in moto con velocità v
in un campo magnetico B vale

 
F  qv  B
In una corrente in un conduttore abbiamo n cariche
per unità di volume, quindi la forza per unità di
volume Fv è

   
Fv  nqv  B  j  B

   
Fv  nqv  B  j  B
Se il conduttore ha lunghezza dl e sezione S e le
cariche si muovono lungo dl (con u versore tangente
al conduttore), la forza dF sul tratto dl vale


  
 
dF  nqS dl v  B  j S dl  B  I dl u  B
 
I dl  B
Quindi la forza dF su un tratto dl del conduttore in cui
passa la corrente I ed è immerso in un campo magnetico
esterno B è
 



dF  Idlu  B  Idl  B
 

Su tutto il conduttore 
F   dF  I  dl  B
condut.
cond .
Forza magnetica su una corrente
elettrica rettilinea
Campo uniforme

FI
 
 
 
 dl  B  I ( Lu )  B  IL  B
cond .
Effetto Hall
L’effetto Hall è la
dimostrazione della forza
sulle cariche che percorrono
un conduttore.
Se prendiamo una lamina
metallica e vi facciamo
passare una corrente I
parallela alla superficie in
un campo B perpendicolare
alla lamina, gli elettroni
vengono spinti nella direzione
Y positivo.
Se i portatori fossero cariche
positive si avrebbe l’effetto
opposto.
Lungo l’asse Y viene a crearsi
un campo elettrico E a causa
dell’accumulo di carica , tale
per cui qE bilancia
la forza



magnetica F  qv  B

 
E  v  B
Campo magnetico generato da una corrente
Una carica elettrica in moto a velocità v genera
un campo magnetico:   qv  u
B
0
r
4
r2
In un filo percorso da corrente ci sono n cariche
per unità di volume che si muovono con velocità v
 
e generano un campo: B
 nqv  u
Vol

0
4
r
r2
Se prendiamo un tratto di filo di sezione S e
lunghezza dl (cioè volume dV=Sdl) il campo
magnetico generato da quel tratto vale:
 




  0 nq( Sdl)v  u r  0 IdluT  u r  0 dl  u r
dB 


I
2
2
4
4
4
r
r
r2
Se un tratto infinitesimo di filo genera un campo
magnetico:
 
 0 dl  ur
dB 
I
4
r2
Il filo completo (il circuito) percorso da una
corrente I genererà il campo magnetico:
 

 0
dl  ur
B   dB 
I 
2
4

r
circuito
circuito
L’espressione è detta
LEGGE DI AMPERE-LAPLACE
ed è stata ricavata sperimentalmente
Il campo magnetico generato da una
corrente rettilinea di lunghezza infinita
 

 0
dl  ur
B   dB 
I
2
4

r
filo
filo
 0
B
I
4
Usando le notazioni della figura:



essendor 
dl
sin 
u 
2
r
R
sin(   )

R
sin
R
essendo  tg (   )  tg
l

0 I
4


sin 
0
0 I 

u
2R
2
sin
R2
R
ltgθ
dl 

R
sin 
2
d


0 I
d

u

sin

d

u

 
2
4R
sin 
0
R

In conclusione il campo magnetico generato
da una corrente rettilinea ha modulo inversamente
proporzionale alla distanza dal filo e ha come
linee di campo circonferenze centrate sul filo.
 0 I 
B
u
2R
Legge di Biot-Savart
Forze magnetiche tra correnti
Quando due fili rettilinei percorsi da correnti I e I’
sono posti parallelamente ad una distanza R l’uno
dall’altro, il filo I genera un campo magnetico B che
agisce con una forza F’ su I’.   I 
B
0
2R
u


  0 I

F '  I ' L' uT  B  I ' L 'u
2R

  0 II '
F '  u R
L'
2R
Due correnti parallele e equiverse come risultato
della loro interazione magnetica si attraggono;
se le correnti hanno versi opposti si respingono.
Le unità di misura elettromagnetiche
Per lo studio delle interazioni elettriche e magnetiche
abbiamo dovuto introdurre:
(i) una nuova grandezza fisica
Q (CARICA ELETTRICA);
(ii) due nuove costanti
e0 (PERMETTIVITA’ ELETTRICA del VUOTO)
0 (PERMEABILITA’ MAGNETICA del VUOTO).
Queste tre quantità non sono indipendenti:
Fissata in modo operativo una di esse le altre sono
derivate.
Scegliamo la strada di fissare l’unità di misura della
corrente elettrica = carica/tempo
[nel S.I. l’Ampere, 1A=1 C/s]
Un AMPERE è la corrente che circola in due
conduttori rettilinei e paralleli, separati dalla
distanza di un metro, che si attirano con una
forza di 2 10-7 N per metro di lunghezza
dei conduttori.