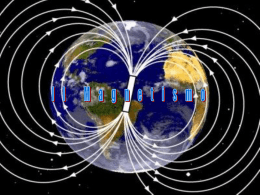
Fenomeni Magnetici
• Campo Magnetico e Forza di Lorentz
• Moto di cariche in campo magnetico
• Momento e campo magnetico di una spira
• Legge di Ampère
• Solenoide
Campo Magnetico
I fenomeni magnetici possono essere
ricondotti all’esistenza di un campo
~ che produce una forza
magnetico B,
magnetica (di Lorentz) F~B sulle sole
cariche in moto: per una carica q che
~
si muove a velocità ~v , F~B = q~v × B
Notare che la forza magnetica non è diretta come il campo ma ortogonale
ad esso! La forza dipende dal segno della carica e dalla sua velocità.
Campo Magnetico II
Nel SI, il campo magnetico si misura in Tesla (T): 1T=1 Volt·s/m2.
Si usa anche il Gauss: 1 G=10−4 T, circa uguale al campo magnetico
sulla superficie terrestre.
In laboratorio si arriva a produrre campi magnetici di qualche decina di
T continui, un migliaio per tempi brevi.
Si possono tracciare le linee di campo
magnetico, come nell’esempio accanto
per il campo magnetico prodotto da
una sbarretta magnetizzata. Hanno un
andamento qualitativamente diverso da
quelle di campo elettrico: non ”escono”
mai da un punto, ma sembrano ”girare”.
Il flusso del campo magnetico su di una superficie
chiusa qualunque è sempre nullo.
Esempio
Elettrone in tubo catodico con velocità v = 8×106
m/s lungo x, sotto campo magnetico B = 0.025
T nel piano xy a 60◦ rispetto all’asse x:
1. Forza magnetica agente sull’elettrone?
2. Scrivere espressione vettoriale per la forza.
• FB = |e|vB sin θ = (1.6 × 10−19)C(8 × 106)m/s(0.025)T(sin 60◦) da
cui FB = 2.8×10−14 N lungo z, verso il basso (la carica dell’elettrone
è negativa)
~ = B(î cos 60◦ + ĵ sin 60◦):
• Scriviamo ~v = v î, B
F~B = −|e|vB î × (î cos 60◦ + ĵ sin 60◦) = −|e|vB sin 60◦k̂
Effetti del campo magnetico
Il campo magnetico produce una forza sulle cariche in moto, ortogonale
sia al campo magnetico che alla direzione di moto della particella. Di
conseguenza, la forza magnetica non fa lavoro sulla particella!
Com’è possibile riconciliare forza magnetica e relatività galileiana? una particella ha
velocità diverse in sistemi di riferimento inerziali diversi! In effetti non è possibile
riconcilare le due cose: dobbiamo sostituire alla relatività di Galileo quella di Einstein.
Una forza ortogonale alla velocità e
costante in modulo produce un moto
circolare uniforme. Il raggio r dell’orbita
(in figura: q > 0, moto in un piano,
campo B che entra nel piano) è dato da:
v2
mv
Fb = qvB = m =⇒ r =
r
qB
Effetti del campo magnetico II
Il campo magnetico esercita una forza su fili percorsi da corrente.
Corrente I = cariche in moto con velocità
media ~vd lungo il filo. Vale la relazione
~vddq = Id~l fra velocità e corrente. Forza
magnetica su un elemento di lunghezza d~l:
~ = Id~l × B.
~
dF~B = dq~vd × B
Per un filo di lunghezza finita, bisogna sommare i vari contributi
infinitesimi:
Z
~
F~B = I d~l × B
L’integrale è fatto lungo il filo. In generale, il campo magnetico può
~ costante ed un tratto di filo di lunghezza l:
variare lungo il filo. Per B
~
F~B = I~l × B
Cariche in campo magnetico
Particelle cariche che penetrano in un
~ uniforme percorrono
campo magnetico B
~
delle spirali, con l’asse lungo B:
la
componente v|| della velocità parallela al
campo magnetico non è influenzata dal
campo e la carica prosegue con moto
rettilineo uniforme in quella direzione.
~ avviene con
Il moto circolare uniforme nel piano perpendicolare a B
velocità angolare ωL (frequenza di Larmor) indipendente dalla velocità
nel piano v⊥:
q
2
mωLr = qωLrB =⇒ ωL = B.
m
mv⊥
p⊥
Il raggio r dell’orbita può essere scritto come r =
=
.
qB
qB
Notare come il raggio dipenda dal rapporto q/m.
Cariche in campo elettrico e magnetico
~ è presente un campo elettrico E,
~ la
Se oltre al campo magnetico B
~ + ~v × B)
~ .
forza agente sulla carica sarà F~ = q(E
~ entra nel piano della pagina.
Esempio: selettore di velocità. Il campo B
~ =E
~ non sono deflesse.
Solo le particelle di velocità v tale che ~v × B
Particelle con velocità differente sono deviate.
Spettrometro di massa
Inviamo le particelle uscite dal selettore di velocità con
velocità v in un secondo campo magnetico.
Le particelle
percorreranno una semicirconferenza con raggio r = mv/qB0:
Si possono cosı̀ distinguere particelle con massa diversa e carica uguale.
Forze e Momento torcente su di una spira
Consideriamo una spira: un circuito chiuso in cui
scorre una corrente I. Per semplicità assumiamo
una spira rettangolare di lati a e b. In un campo
~ costante, la forza totale agente sulla
magnetico B
spira è nulla: lati opposti danno contributi alla
forza totale di verso opposto. Si può dimostrare
che ciò è vero qualunque sia la forma della spira.
C’e’ però un momento torcente che agisce sulla
~ è
spira. Nell’esempio qui a sinistra, in cui B
diretto lungo i lati 1 e 3, il momento torcente è
τ = 2(b/2)(aIB) = (abI)B, dove b/2 = braccio
del momento, aIB = modulo della forza agente
sui lati 2 e 4; ~τ è ortogonale al piano della pagina
e provoca una rotazione in senso orario.
Momento magnetico di una spira
~ forma un angolo θ con la normale
Se B
al piano della spira, il momento torcente
diventa τ = (abI)B sin θ.
~ di modulo
Introduciamo un vettore A
S = ab, superficie della spira, e direzione
ortogonale al piano della spira. Il verso di
~ è scelto secondo la regola della mano
A
destra qui sotto
Introduciamo quindi il momento di dipolo
magnetico:
~
µ
~ = I A.
~ sopra definito.
Questo è un vettore diretto come A
Energia e momento torcente per dipolo magnetico
Si vede immediatamente (e si può dimostrare per spire di forma
qualunque) che il momento torcente agente su di una spira è
~
~τ = µ
~ × B.
Analogamente a quanto fatto per il dipolo elettrico, si può introdurre
l’energia EB potenziale per un dipolo magnetico in un campo magnetico:
~
EB = −~
µ · B.
Questa energia potenziale vale anche per campi magnetici non costanti.
L’ago magnetico della bussola contiene dipoli
microscopici che si allineano nella direzione del
campo magnetico terrestre. Il ”polo nord” di una
spira è determinato dal verso del suo momento di
dipolo magnetico
Chi genera il campo magnetico?
Il campo magnetico è generato da cariche in movimento (Oersted 1812).
Una carica q che viaggia a velocità ~v genera un campo magnetico a
distanza ~r dalla carica:
~v × r̂
~
B = kmq 2
r
dove km è l’analogo magnetico della costante k della legge di Coulomb.
Se una corrente I scorre in un filo, vale la relazione Id~l = ~v dq.
Possiamo allora scrivere
~l × r̂
d
~ = kmI
dB
r2
(legge di Biot e Savart)
~ da
magnetico generato dB
che scorre in una lunghezza
per il campo
una corrente I
d~l di filo.
Campo magnetico di correnti
Cosa è la costante km? Nel SI, si pone
µ 0
2
km ≡
= 10−7Tm/A = 10−7N/A
4π
Storicamente, è tramite questa relazione che si è definito l’Ampère, e
dall’Ampère il Coulomb.
Notare come le linee di campo magnetico
abbiano la forma di linee circolari coassiali
(”girano” attorno al filo). Il verso delle linee
si può determinare usando la regola della
mano destra come in figura.
Applicando la legge di Biot e Savart si può
determinare il campo magnetico prodotto da
una distribuzione di correnti qualunque.
Ordine di grandezza delle forze magnetiche
Le forze magnetiche sono di solito piccole rispetto alle forze elettriche.
Consideriamo due cariche q e q 0 in moto con velocità ~v e ~v 0 parallele. Il
campo generato dalla carica q:
µ ~v × r̂
0
~ =
B
q 2
4π
r
esercita una forza sulla carica q 0 di modulo
µ qq 0
0
0
~ =
Fm = |q 0~v 0 × B|
vv
4π r2
da confrontarsi con la forza elettrica:
1 qq 0
Fe =
.
2
4π0 r
Il rapporto Fm/Fe = µ00vv 0 = vv 0/(3 · 108)2 è molto piccolo per
velocità lontane da quella c della luce (in effetti µ00 = 1/c2).
Campo di un dipolo magnetico
Consideriamo una spira circolare di raggio R percorsa da corrente I.
Il campo su di un punto lungo l’asse è
µ 2~
µ
0
~
B'
4π x3
dove µ
~ = πR2I x̂ è il momento
magnetico della spira.
Le linee di campo escono dal polo Nord ed entrano
nel polo Sud (il polo Nord vede la corrente girare
in senso antiorario). L’energia potenziale EB di una
~ 2, da
spira nel campo di un’altra vale EB = −~
µ1 · B
cui si ricava che poli magnetici opposti si attraggono,
poli magnetici uguali si respingono.
Un grosso dipolo magnetico; la Terra
Per cause tuttora non ben chiare –
probabilmente correnti nel nucleo – la
Terra è un dipolo magnetico di momento
µT ∼ 8 · 1022A m2.
Il campo magnetico terrestre non è
perfettamente allineato con l’asse di
rotazione terrestre, ma forma con esso
un angolo di un po’ più di 11o.
Da notare che che quello che chiamiamo Polo nord è in realtà prossimo
al polo sud magnetico!
Forza fra due fili rettilinei
Consideriamo due conduttori paralleli a distanza a percorsi da correnti
I1 e I2. Il campo generato dal conduttore 2 sul conduttore 1 ha modulo
µ 2I
0
2
B2 =
4π a
e direzione perpendicolare al piano dei due conduttori.
La forza magnetica su di un tratto
infinitesimo del conduttore 1 vale in modulo
µ 2I I
0
1 2
dF = I1B2d` =
d`
4π
a
e quindi, per un tratto di lunghezza `:
µ 2I I
1 2
0
F =
`.
4π
a
Legge di Ampère
Consideriamo un filo rettilineo infinito percorso da una
corrente
µ I.
2IIl campo magnetico generato dal filo vale
0
B=
, diretto tangenzialmente a circonferenze
4π r
coassiali al filo, secondo la regola della mano destra.
L’integrale di lineaIdel campo (circuitazione) su di una
µ 2I
0
~ · d~` =
circonferenza vale
B
(2πr) = µ0I.
4π r
Tale risultato ha validità generale: per un percorso chiuso qualunque,
concatenato a conduttori ove passa una corrente totale I, vale la
I
~ · d~` = µ0I.
B
seguente Legge di Ampère:
E’ l’analogo magnetico del teorema di Gauss in
elettrostatica e ci dà un modo alternativo per
ottenere il capo magnetico dalle correnti.
Campo di un solenoide rettilineo
Un solenoide rettilineo è un insieme di spire avvolte su
di un cilindro. In generale, il campo di un solenoide ha
una forma complessa che ricorda quello di una calamita.
Consideriamo il caso semplice di solenoide rettilineo
infinito, o comunque con diametro piccolo rispetto alla
lunghezza, tramite la legge di Ampère.
Usiamo la legge di Ampère sul percorso 1234 in figura:
I
N
~
~
B · d` = µ0N I =⇒ B = µ0 I
`
assumendo B come in figura (notare le linee di campo).
Con ottima approssimazione, B = µ0nI dentro il
solenoide (n =numero di spire per unità di lunghezza);
B = 0 fuori (pensare al secondo percorso tutto esterno).