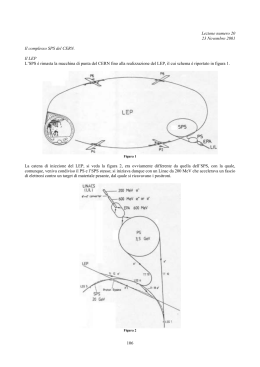
MUTAZIONE: cambio di un bit
Viene effettuata con bassa frequenza, ad es. 1bit ogni 1000
Ha la funzione di recupero di eventuali perdite di informazione
SCHEMI
Indichiamo uno schema con la lettera H
Esempi:
*111*
0*1**
*indica un carattere indeterminato
Il numero di schemi possibili, nel caso di alfabeto binario, è 3l, dove l è la lunghezza della stringa
Il numero di schemi possibili, nel caso di alfabeto di cardinalità K, è (K+1)l
Ordine O(H) dello schema H è il numero di posizioni determinate dello schema.
Lunghezza d(H) dello schema H è la distanza tra la prima e l’ultima posizione determinata
dello schema.
Riproduzione
n=numero totale di stringhe (popolazione)
Ai stringa (individuo)
fi=fitness di Ai
t=tempo (ciclo dell’iterazione)
pi 
Probabilità di riproduzione di Ai:
n
fi t 
 f t 
j
j 1
Probabilità di riprodurre un individuo appartenente allo schema H:
n
n
 piH 
iH 1
fiH t 
n

n

f
iH
t 
iH 1
n
 f t   f t 
iH 1
j 1
j
j 1
j
n
p
iH 1
iH
è una sommatoria estesa ai soli individui appartenenti allo schema H
Indicando con m(H,t) il numero di individui appartenenti allo schema H,
e con f(H,t) la loro fitness media, ovvero:
n
f
iH
t 
f H,t   iH 1
m H,t 
n
f
da cui deriva:
iH 1
n
si potrà scrivere:
p
iH 1
iH
iH
t   f H,t m H,t 
 m H,t 
f  H,t 
n
 f t 
j 1
j
Poiché la popolazione rimane costante nel tempo, la scelta di un individuo per la riproduzione
viene effettuato n volte. Indicando con m(H,t+1) il numero di individui appartenenti allo
schema H al ciclo t+1, si avrà mediamente:
mH,t  1  n  m H,t 
f  H,t 
n
 f t 
j 1
j
n
Indicando con f t  la fitness media della popolazione al tempo t:
si ricava infine:
f  H,t 
mH,t  1  m H,t 
f t 
 f t 
j
f t  
j1
n
Esemplificazione per capire l’andamento nel tempo del numero degli individui appartenenti ai
vari schemi.
Si può scrivere:
f H,t   f t   cf t    f t 1  c
da cui:
f t 1  c 

mH,t  1  m H,t 
 m H,t 1  c
f t 
Nell’ipotesi (molto estrema) di fattore c costante nel tempo (nei vari cicli), si ottiene che la
popolazione al tempo t è data, in funzione di quella iniziale (al tempo 0) dalla relazione:
mH,t   m H,01  ct
Il che significa che se c è negativo (fitness media dello schema minore della fitness media della
popolazione), si ha un decremento esponenziale del numero di individui appartenenti a quello
schema, mentre se c è positivo si ha un incremento esponenziale.
Crossing over
Esempio di taglio in un individuo appartenente al seguente schema:
*1****0
d(H) = 7 - 2 = 5
crossing
over
pd 
Probabilità (data per eccesso) di distruzione pd dello schema H:
Se pc è la probabilità con cui viene effettuato il crossing over :
Probabilità di sopravvivenza ps dello schema H :
d H
l 1
pd  pc
ps  1  pd  1  pc
dH
l 1
d H
l 1
Tenuto conto anche del crossing over, la valutazione (per difetto) della popolazione diviene:
f  H,t  
d H 
mH,t  1  m H,t 
1  pc


f t  
l  1 
Mutazione
Probabilità che una posizione venga mutata : pm
Probabilità che una posizione rimanga immutata : 1 - pm
Probabilità che un individuo, dopo le mutazioni, continui ad appartenere allo schema H :
1  pm o  H 
Se pm << 1, si può scrivere:
1  pm 
oH 
 1  o H  pm
Tenendo conto anche della mutazione, si ottiene infine il teorema degli schemi
o teorema fondamentale degli algoritmi genetici:

f  H,t  
d H 
mH,t  1  m H,t 
1  pc
 oH  pm 


f t  
l 1
Notare che nel prodotto del fattore crossing over con quello della mutazione, è stato trascurato,
poiché piccolo, il termine:
pc
d H
l 1
oH  pm
Sono detti schemi in competizione, quelli con le stesse caratteristiche “geometriche”, ovvero con
fattore


d H 
1  pc
 oH  pm 



l 1
uguale; la variazione nel tempo delle rispettive
popolazioni dipenderà dalla loro fitness media.
Indicando 2 schemi in competizione con a e b, e una loro generica posizione con il pedice i, sono
caratterizzati dalle due alternative:
•ai = bi = *
•ai ≠ * , bi ≠ * con ai ≠ bi in almeno una posizione i
esempio :
*00*
*01*
*10*
*11*
Il numero di schemi in competizione in un gruppo è dato da 2o(H)
Il numero di gruppi diversi di schemi in competizione con lo stesso ordine o(H) è dato da :
 l 


o H 
dove l è la lunghezza della stringa
Il numero totale di gruppi diversi di schemi è dato da : 2l
Efficienza dell’algoritmo genetico
Il numero degli schemi processati può essere valutato come proporzionale a n3, per una
popolazione di n individui rappresentati con alfabeto binario.
Questa caratteristica, per cui con operazioni su n individui si esaminano e sottopongono a
evoluzione un numero proporzionale a n3 schemi, è detta parallelismo implicito.
Dal teorema fondamentale degli algoritmi genetici:

f  H,t  
d H 
mH,t  1  m H,t 
1  pc
 oH  pm 


f t  
l 1
si desume l’altra caratteristica degli algoritmi genetici, ovvero che sono efficienti quando
le soluzioni ottimali del problema sono ottenibili assemblando degli schemi corti, ovvero
con d(H) piccolo.
Questa caratteristica è detta building block hypothesis.
Linee guida nella codificazione del problema
1) Schemi corti e poco correlati con altri schemi che hanno bit definiti lontani nella stringa,
devono essere rilevanti nella soluzione del problema.
2) L’alfabeto usato deve avere bassa cardinalità (possibilmente binario).
Si dimostra che con alfabeto binario si ha un numero di schemi possibili maggiore che con
qualsiasi altra cardinalità.
Poiché il numero di punti dello spazio in cui rappresentiamo il problema è lo stesso:
l
2  K  l' 
lg2 K
l
l'
numero di schemi possibili:
cardinalità 2
cardinalità K
3l
facendo il lg2 del numero degli schemi possibili:
l  lg2 3
lg2 3
ma si ha che
l
 K  1   K  1lg2 K
l'
l
lg2  K  1
lg2 K 
e dividendo per l, si ottiene:
lg2 K  1
lg2 3 
lg2  K 
lg2 K  1
lg2 K 
per K>2
Tests di De Jong
Criteri di valutazione dell’algoritmo genetico
On-line performance:
1 T
xl s   fl t 
T t 1
dove l è l’ambiente (il problema), s la strategia (il particolare algoritmo genetico adottato),
t è il ciclo, T il numero totale di cicli effettuati, f(t) è il valore migliore della funzione di
valutazione al ciclo t.
Off-line performance:
T
1
xl* s   fl * t 
T t 1
dove f*(t) è il valore migliore della funzione di valutazione al ciclo t, tra tutte le esecuzioni
effettuate.
Valutazioni generali sui parametri dell’algoritmo genetico semplice
n grande: migliore off-line performance
Popolazione n
Probabilità di crossing over pc:
Probabilità di mutazione pm:
Sovrapposizione della popolazione G:
n piccolo: migliore on-line performance
0.6  pc  1.0
pm elevato recupera i bit persi, ma diminuisce
la performance (pm =.5 coincide con ricerca
casuale)
G = 1 per ottimizzazioni statiche;
G < 1 per macchina che apprende
Alcune varianti dell’algoritmo genetico semplice
Fattore di affollamento CF: il nuovo individuo generato sostituisce il più simile scelto
in un gruppo di CF individui della vecchia popolazione.
Scalatura della funzione di valutazione:
f'  af  b
dove f è la funzione originaria
a e b sono determinati in modo che soddisfino le condizioni:

f  f

  cf   cf
f MAX
 af  b  f

af MAX  b  cf
Risolvendo:
f
denominatore:
f MAX
1
 f  f MAX
1
numeratore per trovare a:
f
cf
1
 f  cf  f 1  c 
1
f 1  c 
f  c  1
a

f  f MAX f MAX  f
f
numeratore per trovare b:
f MAX
f
 cf 2  f MAX f  f cf  f MAX 
cf
f cf  f MAX 
 f MAX  cf 
b
 f
f  f MAX
f MAX  f
Possibile situazione iniziale
Possibile situazione finale
NICCHIA e condivisione tra gli individui delle risorse della nicchia
Funzione di “sharing”
Siano dati due individui xi e xj, si definisce una distanza d(xi, xj), tale che:
d(xi, xi) = 0 valore minimo quando i 2 individui sono =
d(xi, xj)
d(xi, xj) = 1 valore massimo per i 2 individui più
differenti in tutta la popolazione
La distanza si ottiene dal n° di bit diversi normalizzato per il valore MAX
Si definisce una funzione di sharing s[d(xi, xj)] , che segue la seguente legge:
La funzione di valutazione fs, viene ottenuta
dalla funzione originaria f modificata tramite
la funzione di sharing:
1
fs xi  
s[d(xi,xj)]
n
 sdx , x 
j 1
0
d(xi,xj)
f xi 
1
dove n è la popolazione
i
j
Capacità adattativa degli algoritmi genetici
Si intende la capacità di adattarsi a trovare soluzioni ad un problema che cambia nel tempo
Viene incrementata con i seguenti accorgimenti:
1) mantenimento di soluzioni di precedenti cicli:
a) fattore di affollamento CF, che diversifica le soluzioni
b) G < 1, che mantiene individui dei cicli precedenti
2) inserire la capacità di evoluzione nello stesso algoritmo,
introducendo nella stringa dell’individuo i parametri di
controllo pc, pm, G, che quindi possono essere modificati
nel tempo
Applicazioni nell’ambito chimico
•Interpretazione di cromatogrammi complessi
•Interpretazione di spettri NIR
•Docking di complessi supramolecolari
•Energia di correlazione per modello LDA nel metodo DFT
•Studio di cinetiche di combustione
•Generazione di strutture che rispettino i dati NMR
•Previsione di strutture secondarie di RNA
•Ottimizzazione della conformazione di catene laterali di proteine globulari
•Previsione delle modificazioni strutturali a seguito di sostituzione di catene
laterali (mutazione) in proteine (ingegneria genetica)
•Tentativi di previsione di struttura terziaria in proteine, a partire dalla conoscenza
della sequenza primaria