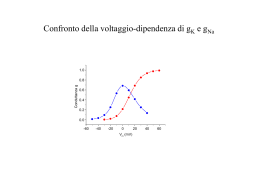
Trasporti mediati: Calcolo della costante di affinità ka
F max
20
Flusso netto [moli/(cm s]
2
15
F
10
5
F max
ka
1
C
0
0
50
100
150
200
DC (mM)
15
F max
2
10
5
0
ka3
0 ka1
ka2
10
DC (mM)
20
30
20
Se si vuole costruire un grafico che
rappresenti un range di
concentrazioni molto ampio (alcuni
ordini di grandezza) conviene usare
una scala logaritmica
15
Flusso
2
Flusso netto [moli/(cms]
20
10
5
S
S+Ic
0
0.01
0.1
1
10
[S]
100
1000 10000
Calcolare analiticamente la concentrazione di substrato S alla quale il
flusso f è pari al 60% di Fmax.
Cosa occorre sapere:
Fmax
1) che f 
1 Km [ S ]
2) i valori di Fmax e Km.
Se Fmax = 120 mM/s/mm2
e Km = 10 mM
Allora: S 
f
Fmax  f
 Km 
72
 10  15mM
120  72
Equazione di Nernst
 [ I ]est
58mV
E
 Log10 
z
 [ I ] int
Ki (mM)
Ke (mM)
EK (mV)



100
1
-116
100
10
-58
100
100
0
Nai (mM)
Nae (mM)
ENa (mV)
1
100
116
10
100
58
100
100
0
Cli (mM)
Cle (mM)
ECl (mV)
140
10
-66
140
50
-26
140
140
0
Controllare la valenza dello ione!!!!!!
Circuiti equivalenti
Dati:
1)
Trovare:
ENa=+45mV; EK= -80mV; ECl= -20mV; gNa=20mS; gK=60mS; gCl=10 mS
Vm=…..
2) Vm= -40mV; ENa=+50mV; EK= -70mV; ECl= -20mV; gNa=10mS; gCl=gK/4
gK=…..
Risposte
1
2
Vm

gNaENa gK EK
gNa gK
Vm  46mV
( gNa  gK  gCl ) Vm  ENa  gNa  EK  gK  ECl  gCl
( g Na  x 
x
x
) Vm  ENa  g Na  EK  x  ECl 
4
4
x  36mS
Occhio alle unità di misura!!!!!
10nA/100mV=10 · 10-9A / (100 · 10-3)V=10-7=0.1 · 10-6 S=0.1 mS
50pA/20mV=50 · 10-12A /( 20 · 10-3)V=2.5 · 10-9 S=2.5nS
5nS · 20mV=5 · 10-9S· 20 · 10-3V=100 · 10-12 A=10-10A=100pA
20mS · 20mV=20 · 10-3 S· 20 · 10-3V=400 · 10-6 A=4 · 10-4A=0.4mA
Costante di tempo
Calcolare la costante di tempo di membrana sapendo
che Rm=1 MW e Cm=3 nF.
Un neurone, in seguito ad un’iniezione di corrente,
varia Vm da Vo = –70 mV a Vf = –60 mV. Sapendo che
la costante di tempo di tale neurone è t3ms, dopo
quanti ms Vm avrà raggiunto un valore di –62 mV.
tm = Rm·Cm = 1 MW·3 nF = 3 ms
L’equazione che definisce, istante per istante, il valore di Vm al
t
variare del tempo t è:
t
Vm  Vo  (Vf  Vo )  (1  e )
ovvero:
Vo = –70 mV
Dati:
t
Vm  Vo  (Vf  Vo )  (1  e t )
Vf = –60 mV
 62 
t
70  ( 60  ( 70))  (1  e 3
 62 
t
60  10  e 3
t
e3
1

5
e t  53
ln(e )  ln(125)
t  ln(125)  4.83ms
t
)
Vm= –62 mV
 62  70 
t = 3 ms
t
( 60  70)  (1  e 3
t
8
 1 e 3
10
t
e3
t
e3
 1
8
2

10 10
10
 5  e t  53
2
ln(e t )  ln(125)
t  ln(125)  4.83ms

)
Costante di spazio
Calcolare la costante di spazio di un assone sapendo che
Rm=1 MW·cm e Ri=104 MW/cm.
Un assone, in seguito ad uno stimolo di corrente, modifica il
suo potenziale di membrana nel punto xo al valore finale
Vf=-60 mV. V subirà un decadimento allontanandosi da xo
fino a ritornare al suo valore di riposo Vo=-80mV. Sapendo
che la costante di spazio di quel neurone è l=0.1 mm,
calcolare a quale distanza da xo V sarà decaduto a –70 mV.
lm = √(Rm/Ri) = √(1 MW·cm/104 MW/cm) = 0.01 cm = 0.1 mm
l=0.1 mm
Dati: Vo=-80 mV; Vf=-60 mV; Vm=-70 mV
 x 
L’equazione che definisce il decadimento


 l 
del segnale al variare della distanza x è: Vm  Vo  (Vf  Vo )  e
 70  80  ( 60  80)  e
 x 
 x 


 0.1


10
 0.1
e
20
x
 10 
ln   
0.1
 20 
 20 
x  0.1 ln   0.1 ln 2  0.069mm
 10 
Canali voltaggio-indipendenti
Il potenziale di riposo di una cellula è determinato dalla presenza
di due canali permeabili rispettivamente ai cationi A+ e B+
attraverso i quali passano le correnti ioniche IA e IB indicate in
tabella.
Dopo aver disegnato i rispettivi grafici I/V, determinare:
1) le conduttanze gA e gB;
2) il potenziale di equilibrio dei due ioni A e B;
4) il potenziale di riposo Vr della cellula.
V(mV)
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
IA (nA)
-1650
-1100
-550
0
550
1100
1650
2200
2750
3300
V(mV)
-20
-10
0
10
20
30
40
50
60
70
IB (nA)
-1320
-1100
-880
-660
-440
-220
0
220
440
660
V(mV)
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
IA =gA (V-EA ) (nA)
-1650
-1100
-550
0
550
1100
1650
2200
2750
3300
gA
V(mV)
-20
-10
0
10
20
30
40
50
60
70
55
55
55
55
55
55
55
55
55
IB=gB(V-EB) (nA)
-1320
-1100
-880
-660
-440
-220
0
220
440
660
gB
4000
22
22
22
22
22
22
3000
2000
EA
EB
1000
-
0
22
22
22
-150
-100
-50
0
50
100
-1000
-2000
Il valore della conduttanza si ricava applicando la
legge di Ohm modificata:
g
g1A = [-1650]/[-120-(-90)] = -1650/[-120-(-90)] = 55 mS
I1
V1 E
g1B = [-880]/[0-(40)] = -880/(-40) = 22 mS
60
EA= -90mV  è quel valore del potenziale al quale IA=0
50
EB= +40mV  è quel valore del potenziale al quale IB=0
gA
40
gB
30
20
10
0
-140 -120 -100 -80 -60 -40 -20
Potenziale di riposo:
V r = (EAg A+E Bg B)/(g A+g B) =
-52.9
mV
0
20
40
60
80
Canali voltaggio-dipendenti
Dati i valori di IK nell’intervallo di potenziali tra –80 e +80 mV,
sapendo che EK= -85 mV, calcolare:
1) il valore della conduttanza massima GK allo stato stazionario;
2) qual è la probabilità che siano aperti a –10 mV?
3) Se non c’è inattivazione e i canali presentano 3 gates di
attivazione, qual è la probabilità che la singola gate n sia
aperta?
Vm -EK
5
15
25
35
45
55
65
75
85
95
105
115
125
135
145
155
165
gK
0.002
0.006
0.018
0.053
0.158
0.450
1.139
2.300
3.461
4.150
4.442
4.547
4.582
4.594
4.598
4.599
4.600
EK = -85 mV
I=g(V-E)  g=I/(V-E)
800
nS
IK
0.0
0.1
0.4
1.9
7.1
24.7
74.1
172.5
294.2
394.3
466.4
522.9
572.8
620.2
666.7
712.9
759.0
5.0
pA
Vm
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
4.0
600
3.0
400
2.0
200
1.0
0.0
0
-100
-50
0
50
-100
100
-50
0
50
100
mV
mV
Se non c’è inattivazione e i canali presentano 3 gates di
attivazione, qual è la probabilità che siano aperti a –10 mV?
E che la singola gate n sia aperta?
a -10 mV  g=172.5/(-10+85)=2.3 nS
Po=g/Gmax=2.3/4.6=0.5
3 gates  Po=n3  n=3√(Po)= 3 √(0.5)=0.79
a +70 mV  g=712.9/(70+85)=4.6 nS
a +80 mV  g=759/(80+85)=4.6 nS
} g=G
max
Voltaggio-dipendenza – 1a parte
A) Lavorando in condizioni di voltage-clamp Hodgkin e Huxley trovarono
che, dopo una particolare depolarizzazione dal potenziale Vo al potenziale
finale Vf (=-10 mV), il parametro che identifica la gate “n” di attivazione del
canale del K+ aveva il seguente andamento temporale:
n = 0.81 [ 1- exp(-t / 1.1) ],
dove t e’ espresso in msec.
1) Sapendo che la conduttanza massima GK e’ 25 mS, mettere in grafico la
conduttanza gK in funzione del tempo ad intervalli di 1 msec per una durata
totale di 10 msec.
2) Qual’e’ il valore di gK allo stato stazionario (gK)?
Per calcolare gK occorre sapere che, secondo il modello di H&H, il canale del K delayedrectifier è costituito da 4 gates dell’attivazione identiche e indipendenti. Quindi, se n è la
probabilità di apertura di una singola gate, la probabilità di apertura contemporanea delle 4
gates è n4, e corrisponde alla probabilità di apertura dell’intero canale.
Occorre inoltre sapere che: gK=Gmax · n4
Infine, Il testo ci dice che Gmax=25 mS
12
10
n(t)
n4(t)
g (nS)
0
0
0
0
1
0.484
0.055
1.37
2
0.679
0.212
5.30
3
0.757
0.328
8.21
4
0.789
0.387
9.67
5
0.801
0.412
10.31
6
0.807
0.423
10.58
7
0.809
0.428
10.69
8
0.809
0.429
10.73
9
0.810
0.430
10.75
10
0.810
0.430
10.76
11
0.810
0.430
10.76
12
0.810
0.430
10.76
8
g (nS)
t (ms)
6
4
2
0
-1
1
3
5
7
9
11
13
tempo (ms)
Il valore della conduttanza allo stato
stazionario tende asintoticamente ad un
valore costante
Cosa occorrerebbe conoscere per calcolare anche la
corrente stazionaria IK a quel potenziale (-10 mV)?
IK=g·(V-EK)
quindi occorrerebbe conoscere EK (-80 mV)
Voltaggio-dipendenza – 2a parte
B) In seguito alla stessa depolarizzazione da Vo a Vf, i parametri “m” e “h”
relativi al canale del Na voltaggio-dipendente seguivano invece i seguenti
andamenti temporali:
m = 0.9 [1 – exp(-t / 0.2) ],
h = 0.8 exp(-t / 0.8 ),
dove t e’ espresso in msec.
1) Sapendo che la conduttanza massima GNa e’ 70 mS, mettere in grafico gNa
in funzione del tempo, ad intervalli di 0.5 msec per una durata totale di 5
msec.
2) Qual’e’ il valore massimo raggiunto da gNa in questo intervallo di tempo?
Per calcolare gNaoccorre sapere che, secondo il modello di H&H, il canale del Na è costituito
da 3 gates dell’attivazione identiche e indipendenti e da una gate dell’inattivazione. Quindi,
se m è la probabilità di apertura di una singola gate dell’attivazione e h la probabilità di
apertura della gate dell’inattivazione, la probabilità di apertura contemporanea delle 3 gates
m e della gate h è m3·h,e corrisponde alla probabilità di apertura dell’intero canale.
Occorre inoltre sapere che: gNa=Gmax · m3·h
1.0
Infine, Il testo ci dice che Gmax=70 mS
0.8
0.6
Il valore massimo di gNa corrisponde al picco
del grafico 2
m
h
0.4
m3*h
0.2
t (ms)
m
m3
h
m3*h
g(t) (mS)
0
0.000
0.000
0.800
0
0.00
0.2
0.569
0.184
0.623
0.114721
8.03
0.5
0.826
0.564
0.428
0.241
16.90
1
0.894
0.714
0.229
0.164
11.46
1.5
0.900
0.728
0.123
0.089
6.25
2
0.900
0.729
0.066
0.048
3.35
2.5
0.900
0.729
0.035
0.026
1.79
3
0.900
0.729
0.019
0.014
0.96
12
3.5
0.900
0.729
0.010
0.007
0.51
8
4
0.900
0.729
0.005
0.004
0.28
4.5
0.900
0.729
0.003
0.002
0.15
5
0.900
0.729
0.002
0.001
0.08
0.0
0
1
2
3
4
5
6
g(V) (mS)
20
16
4
0
0
1
2
3
4
5
6
Sommazione spaziale di PPS
Il neurone al centro riceve cinque terminali sinaptici da altrettanti neuroni ciascuno dei
quali forma più contatti sinaptici (il terminale f1 forma tre contatti, cinque f2, ecc.). Il
terminale f4 libera un neurotrasmettitore che genera potenziali postsinaptici inibitori,
mentre i potenziali postsinaptici generati dagli altri terminali sono eccitatori. Se il
potenziale di riposo del neurone bersaglio è –70 mV e la soglia di eccitamento è posta a –
55 mV, generando ciascuna sinapsi un potenziale postsinaptico di 1 mV in valore
assoluto, stabilire se quel neurone può generare un potenziale d’azione quando tutte le
sinapsi sono attivate contemporaneamente.
Vriposo= -70 mV
Vsoglia= -55 mV
PPS= 1 mV in valore assoluto
PPSE= +1 mV (depolarizzazione; f1, f2, f3, f5)
PPSI= -1 mV (iperpolarizzazione; f4)
Supponiamo che i PPS si sommino completamente tra di loro.
f1, f2, f3, f5→PPSE →(3+5+8+3) x 1 mV= +19 mV
f4 →PPSI →8 x (-1 mV)= -8 mV
Il potenziale somma sarà: +19 -8= +11 mV
-70 +11= -59 mV (< -55 mV) → non viene raggiunta la soglia
→non viene generato un potenziale d’azione
Per poter generare un PdA dovrebbero essere attivi solo 4 input
inibitori
Esempio numerico di innalzamento del contrasto mediante inibizione laterale
GSE=guadagno sinapsi eccitatorie
GSi=guadagno sinapsi inibitoie
L’inibizione laterale causa un
aumento significativo del contrasto