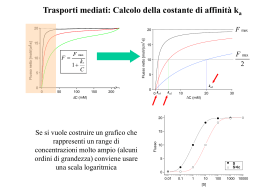
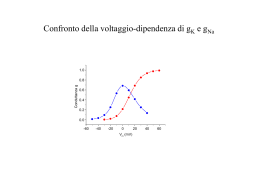
Attività elettrica dei
neuroni
Neuroni piramidali del SNC che stanno crescendo su una matrice di glia/fibroblasti
Nel potenziale d’azione si distinguono due fasi:
-fase di DEPOLARIZZAZIONE
-fase di RIPOLARIZZAZIONE
tempo
Basi ioniche del potenziale d’azione
• conduttanze e correnti di Na voltaggio-dipendenti
• conduttanze e correnti di K voltaggio-dipendenti
Qual è il ruolo dei canali del Na+ nella genesi del potenziale d’azione?
1. Osservazione di Hodgkin e Huxley (1939):
– al picco di un potenziale d’azione il potenziale di membrana diventa
transitoriamente positivo all’interno – overshoot.
2. Ipotesi: è coinvolto il Na
– l’entrata di Na attraverso la membrana continuerà fino al raggiungimento
del potenziale di equilibrio del Na (ENa).
ENa = 58 log ([Na]o / [Na]i) = 58 log (460/50) = 59 mV
50% [Na]o -> ENa = 38 mV
33% [Na]o -> ENa = 28 nV
3. Esperimento di Hodgkin e Katz (1949):
riducendo [Na]o  riduzione dell’overshoot
Conclusione:
Il potenziale d’azione è il risultato di un
grande e transitorio aumento nella
permeabilità al Na della membrana.
Al potenziale di riposo
Al picco del PA
PK : PNa : PCl
1.0: 0.04: 0.45
1.0 : 20 : 0.45
Che dire della fase di caduta del potenziale d’azione?
- I canali del Na semplicemente si chiudono (inattivazione)
Ma se la causa fosse solo questa, la ripolarizzazione sarebbe più lenta di quanto
osservato sperimentalmente
- Si verifica un successivo grosso aumento della permeabilità della membrana al K
dovuto all’apertura di canali del K voltaggio-dipendenti.
Il potenziale di membrana ritorna verso EK
Il potenziale di membrana iperpolarizza (diventa più
negativo del potenziale di riposo) per un certo tempo
Per spiegare l’ampiezza e l’andamento temporale del potenziale d’azione
Ipotesi: Le conduttanze del Na e K sono voltaggio-dipendenti
- La probabilità che i canali si aprano aumenta con la depolarizzazione.
L’effetto della conduttanza al Na
- rigenerativo.
Il processo
-si autoalimenta
-feedback positivo
La depolarizzazione aumenta la
conduttanza al K con un certo ritardo.
Aumento
di gNa
Depolarizz.
Corrente di
Na entrante
Aumento
di gK
-autolimitante
-feedback negativo
Depolarizz.
Corrente di
K uscente
Ripolarizz.
Ipotesi di Hodgkin e Katz:
La depolarizzazione della cellula al di sopra del valore di soglia causa un breve aumento
della permeabilità della membrana agli ioni Na.
In che maniera la permeabilità di membrana (conduttanza) agli ioni Na varia con il potenziale di membrana?
gNa = INa / (Vm – ENa)
Esperimento: Occorrerebbe misurare l’ampiezza della
corrente di Na+ (INa) che fluisce attraverso la membrana
a diversi livelli del potenziale di membrana (Vm)
C’è un problema: La corrente fluisce
attraverso la membrana  il potenziale
di membrana cambia  la conduttanza
della membrana si modifica sia al
variare del potenziale di membrana che
nel tempo
Cioè, esiste forte interdipendenza del
PM e del gating dei canali del Na (e del
K)  sia il PM che la conduttanza dei
canali cambiano costantemente.
depolarizzazione
INa entra.
Per risolvere questo problema,
K. Cole sviluppò la tecnica del
voltage-clamp.
Canali Na
aprono
Alcuni tipi di canali Ionici sono sempre aperti, altri no!
extracell.
intracell.
Sempre
aperti
Il loro comportamento è
ohmico: la relazione I/V è
lineare  g=costante
Voltaggio-dipendenti:
rispondono a
variazioni di Vm
Il loro comportamento non
è ohmico: la relazione I/V
non è lineare perché g
non è costante [g=f(Vm)]
Modello del gating secondo H&H
Il modello di H&H della gate assume una reazione cinetica del 1o
ordine tra gli stati aperto e chiuso della particella di gating
a
C
O
b
Quindi, la probabilità della particella di trovarsi nello stato
aperto può essere descritta da:
(1-Po)
a
b
Po
Trattandosi di una cinetica del 1o ordine, sarà:
dPo
 a (1  Po )  bPo
dt
Allo stato stazionario (equilibrio) sarà:
a
quindi,
P 
o
dPo
 a (1  Po )  bPo  0
dt
ab
Risolvendo l’equazione differenziale del 1o ordine e applicando
la condizione al contorno Po0  Po(t  0), si ottiene:


Po( t )  Po0  ( Po  Po0 ) 1  e ( a  b )t

1/(ab)=t rappresenta la costante di tempo dell’attivazione ed è
un indice della velocità di attivazione della particella di gating.
Se p particelle di gating indipendenti
sono coinvolte nel gating del canale,
allora il canale seguirà il seguente
andamento temporale: Pochann (t )  Po(t )p
Prob. Di Attivaz.
1.0
Po(t)
0.8
0.6
[Po(t)]p
0.4
0.2
0.0
0
2
4
Tempo
6
8
La tecnica del voltage-clamp consiste nel bloccare il potenziale di membrana
ad un valore costante nel tempo e nel registrare le correnti ioniche
transmembranarie generate a tale potenziale di membrana
Potenziale di membrana
finale (Vm) costante
(potenziale di comando)
(mV)
20
Potenziale di riposo (Vr)
-70
0
10
20
Tempo (ms)
30
40
Corrente ionica (nA)
60
Corrente transmembranaria
generata dal passaggio di
Vm da –70 mV a +20 mV
40
20
0
-20
-40
-60
0
10
20
30
40
Tempo (ms)
Vantaggi del voltage-clamp:
In genere, nel caso di canali voltaggio-dipendenti, gm = f(V,t) ma,
1.
Vm è bloccato ad un valore costante  gm = f(t) soltanto e può essere dedotto dall’andamento
della corrente ionica Ii
2.
E’ possibile separare Ii da Ic. Infatti cm è caricata istantaneamente
Voltaggio (mV)
Separazione farmacologica delle correnti IK e INa
20
-70
0
10
20
Tempo (ms)
30
40
+ TTX (IK)
INa+IK
Corrente ionica (nA)
60
40
20
0
+ TEA (INa)
-20
-40
-60
0
10
20
Tempo (ms)
30
40
Voltaggio-dipendenza dei canali Kv
140
120
100
+
I(K ) max (nA)
Voltaggio (mV)
60
50
40
30
20
10
0
-10
-20
-30
80
60
40
IK=gK• (V-EK)
20
0
-70
0
10
20
30
-20
40
-30 -20 -10 0
Tempo (ms)
10 20 30 40 50 60
Voltaggio (mV)
140
1.0
120
Conduttanza (μS)
Corrente K + (nA)
100
80
60
40
0.8
0.6
0.4
gK = IK/(V-EK)
20
0.2
0
0.0
-20
0
10
20
Tempo (ms)
30
40
EK=-80 mV
-30 -20 -10 0
10 20 30 40 50 60
Voltaggio (mV)
Canali voltaggio-indipendenti
Il potenziale di riposo di una cellula è determinato dalla presenza
di due canali permeabili rispettivamente ai cationi A+ e B+
attraverso i quali passano le correnti ioniche IA e IB indicate in
tabella.
Dopo aver disegnato i rispettivi grafici I/V, determinare:
1) le conduttanze gA e gB;
2) se i due canali sono voltaggio-dipendenti o -indipendenti;
3) il potenziale di equilibrio dei due ioni A e B;
4) il potenziale di riposo Vr della cellula.
V(mV)
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
IA (nA)
-1650
-1100
-550
0
550
1100
1650
2200
2750
3300
V(mV)
-20
-10
0
10
20
30
40
50
60
70
IB (nA)
-1320
-1100
-880
-660
-440
-220
0
220
440
660
V(mV)
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
IA =gA (V-EA ) (nA)
-1650
-1100
-550
0
550
1100
1650
2200
2750
3300
V(mV)
-20
-10
0
10
20
30
40
50
60
70
IB=gB(V-EB) (nA)
-1320
-1100
-880
-660
-440
-220
0
220
440
660
4000
3000
2000
EA
1000
0
-150
-100
-50
0
-1000
-2000
EA=-90mV
EB=+40mV
EB
g1A=-1650/[-120-(-90)]=
g1B=-1320/[-20-(+40)]=
55
mS
22
mS
Vr=(E AgA+EBgB)/(g A+gB)= -52.9 mV
50
100
Quesito del giorno
Un ricercatore, in seguito ad esperimenti condotti in voltageclamp ha ricavato che la corrente di K+ (IK) dipende dal potenziale
di membrana (V) secondo la seguente relazione:
1


IK  4.6  (V  85)   1 
(V 10) / 9 
 1 e

(pA)
1) Calcolare i valori di IK nell’intervallo di potenziali tra –80 e
+80 mV ad intervalli di 10 mV e metterli in grafico in funzione di
V;
2) Dai valori di IK ricavati, e sapendo che EK= -85 mV, calcolare i
valori corrispondenti di gK e metterli in grafico in funzione di V;
3) A quale valore di V sara’ aperta la meta’ dei canali?
IK = 4.6·[1-1/(1+EXP((V+10/9))]·(V+85)
(pA)
EK = -85 mV
IK
0.0
0.1
0.4
1.9
7.1
24.7
74.1
172.5
294.2
394.3
466.4
522.9
572.8
620.2
666.7
712.9
759.0
Vm -EK
5
15
25
35
45
55
65
75
85
95
105
115
125
135
145
155
165
gK
0.002
0.006
0.018
0.053
0.158
0.450
1.139
2.300
3.461
4.150
4.442
4.547
4.582
4.594
4.598
4.599
4.600
600
400
200
0
-100
-50
0
50
100
mV
nS
Vm
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
pA
800
5.0
4.0
3.0
2.0
1.0
0.0
-100
-50
0
mV
50
100
Voltaggio-dipendenza dei canali Na
1
0
40
30
20
10
0
-10
-20
-30
-40
-50
-1
I(Na) picco (nA)
Voltaggio (mV)
60
-2
-3
-4
-6
-70
-7
0
1
2
3
4
-50 -40 -30 -20 -10 0 10 20 30 40
0
-1
-2
-3
-4
-5
0.12
gNa = INa/(VENa)
0.10
ENa=+50 mV
0.14
0
1
2
Tempo (ms)
3
4
0.08
0.06
0.04
0.02
0.00
-50 -40 -30 -20 -10 0 10 20 30 40
0
1
2
Tempo (ms)
60
Voltaggio (mV)
Conduttanza (μS)
I(Na) (nA)
I(Na) (nA)
Tempo (ms)
0
-1
-2
-3
-4
-5
-6
-7
INa=gNa• (V-ENa)
-5
3
4
Voltaggio (mV)
Separazione della fase di attivazione della corrente
di Na dall’inattivazione
La pronasi rimuove l’inattivazione
Voltaggio (mV)
-80
-60 -40
Corrente di Na (nA)
Voltaggio (mV)
40
30
20
10
0
-10
-20
-30
-40
-50
-60
-70
-80
-90
-20
0
0
20
40
-200
-400
-600
-800
0
10
20
30
40
tempo (ms)
0
2.5
-200
2.0
-400
-600
-800
-1000
1.5
0.5
1.0
0.5
-1200
0
0
10
20
tempo (ms)
30
40
0
-80
-60
-40
-20
0
Voltaggio (mV)
20
40
Prob. canale aperto
Conduttanza ( m S)
Corrente (nA)
1
L’ampiezza della corrente di K aumenta con la depolarizzazione.
L’ampiezza della corrente di Na aumenta e poi diminuisce con la depolarizzazione.
Perchè?
Depolarizzazione:
Depolarizzazione:
IK= gK (Vm–EK)
INa= gNa (Vm–ENa)
La corrente attraverso il canale dipende da
1. Permeabilità del canale: conduttanza
le conduttanze del Na e K sono voltaggio-dipendenti
2. Driving force – dovuta al potenziale elettrico attraverso
la membrana e al gradiente di concentrazione degli ioni.
Come risalire dai valori di conduttanza allo stato stazionario
alla probabilità di trovare una singola gate del canale aperta
Grafico della conduttanza g(V) allo stato stazionario
Nel caso di un canale inattivante, esso è stato ottenuto
rimuovendo l’inattivazione
2.5
Gmax
1.5
0.5
1.0
0.5
0
Prob. canale aperto
C onduttanza ( m S)
1
2.0
0
-80 -60 -40 -20
0
20
g  (V )  Po
g
P 
Gmax

o
40
Voltaggio (mV)
Ipotesi: l’attivazione del canale è regolata da x gates n uguali e indipendenti.
Allora, se n∞ è la probabilità di avere la singola gate n aperta allo stato stazionario, la probabilità Po di
trovare il canale aperto allo stato stazionario (in assenza di inattivazione) sarà:
Po  n
x
Probabilità composta: n·n·n…. (x volte)
Quindi, dai valori di Po si può risalire ai valori di n∞:
n  x Po
Quesito del giorno
Un ricercatore, in seguito ad esperimenti condotti in voltageclamp e utilizzando la tossina di scorpione per bloccare
l’inattivazione, ha ricavato che la conduttanza del canale del
Na+ (gNa) dipende dal potenziale di membrana (V) secondo la
seguente relazione:
1

 (nS)
gNa  5.6   1 
(V  30) / 6 
 1 e

1) Calcolare i valori di gNa nell’intervallo di potenziali tra –
80 e +80 mV ad intervalli di 10 mV e metterli in grafico in
funzione di V; a quale valore di gNa sarà aperta la metà dei
canali?
2) Dai valori di gNa ricavati, e sapendo che ENa= +55 mV,
calcolare i valori corrispondenti di INa e metterli in grafico in
funzione di V.
(nS)
ENa=+55 mV
nS
gNa=5.6(1-1/[1+EXP((V+30)/6)])
6.0
5.0
4.0
gNa (nS)
0.00
0.01
0.04
0.19
0.89
2.80
4.71
5.41
5.56
5.59
5.60
5.60
5.60
5.60
5.60
5.60
5.60
Vm -ENa
-135
-125
-115
-105
-95
-85
-75
-65
-55
-45
-35
-25
-15
-5
5
15
25
INa (pA)
-0.2
-0.9
-4.3
-20.3
-84.5
-238.0
-353.3
-351.5
-305.9
-251.7
-196.0
-140.0
-84.0
-28.0
28.0
84.0
140.0
3.0
2.0
1.0
0.0
-100
-50
0
50
100
50
100
mV
pA
Vm
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
200
100
0
-100
-50
-100
0
-200
-300
-400
mV
Studio dell’inattivazione allo stato stazionario
0 mV
1.2
-60
-80
-100
-120
0
1
2
3
4
Tempo (ms)
5
6
7
0.2
0.0
1.0
0.8
0.6
0.5
0.4
0.2
0.0
-0.2
-120
-0.4
INa (nA)
1
-40
Corrente di Na (nA)
Vm (mV)
-20
-0.6
-0.8
-1.0
-1.2
0
1
2
3
4
Tempo (ms)
5
6
7
Probabilità gate h aperta
0
0
-100
-80
-60
-40
-20
Potenziale di condiz. (mV)
0
Se si ipotizza che il processo di inattivazione
sia regolato da un’unica gate (h), i valori in
grafico sono proporzionali alla probabilità di
trovare tale gate aperta allo stato stazionario
Confronto della voltaggio-dipendenza di gK e gNa
1.0
Conduttanza g
0.8
0.6
0.4
0.2
0.0
-60
-40
-20
0
Vm (mV)
20
40
60
Nota:
A parità di conduttanza, è la driving force che determina
l'andamento della relazione I/V
EA =+55mV
Vm
-80
-60
-40
-20
0
20
40
60
80
g (nS)
0.00
0.04
0.89
4.71
5.56
5.60
5.60
5.60
5.60
Vm -EA
-135
-115
-95
-75
-55
-35
-15
5
25
EB=-80mV
IA (pA)
-0.2
-4.3
-84.5
-353.3
-305.9
-196.0
-84.0
28.0
140.0
Vm -EB
5
25
45
65
85
105
125
145
165
1000
800
EA=+55mV
EB=-80mV
Corrente (pA)
600
400
200
0
-200
-400
-100 -80 -60 -40 -20
0
20
Voltaggio (mV)
40
60
80 100
IB (pA)
0.0
0.9
40.0
306.2
472.8
587.9
700.0
812.0
924.0
HHsim: Graphical Hodgkin-Huxley Simulator
http://www.cs.cmu.edu/~dst/HHsim/
Esercizio
Usando il programma di simulazione H&H, progettare un
esperimento di voltage-clamp per determinare:
(a) Il potenziale di inversione della corrente del Na
(b) Il potenziale di inversione della corrente del potassio
Calcolo del potenziale di inversione (equilibrio) della corrente di K+
80
60
Vtail (mV) IK ist. (nA)
Voltaggio (mV)
40
20
0
-20 0
5
10
15
20
25
30
35
-40
V-EK
-60
348
-60-EK >0
-70
60
-70-EK >0
-80
-216
-80-EK <0
 EK < -60
 EK < -70
 EK > -80
-60
-80
-100
Tempo (ms)
Relazione IK ist. - Voltaggio
400
4000
IK (nA)
3000
2000
1000
0
-1000 0
5
10
15
20
25
30
35
-2000
IK istantanea (nA)
5000
EK
300
200
100
0
-85
-80
-75
-70
-100 -55
-300
Tem po (m s)
Voltaggio (mV)
IK (nA)
-60
-200
-3000
500
400
300
200
100
0
-100 24
-200
-300
-400
-500
-65
+348 nA (-60 mV)
+60 nA (-70 mV)
25
26
27
-216 nA (-80 mV)
Tempo (ms)
28
29
30
C
O