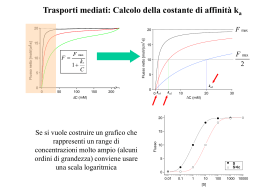
Attività elettrica dei
neuroni
Neuroni piramidali del SNC che stanno crescendo su una matrice di glia/fibroblasti
Un esperimento in current-clamp
Si inietta una corrente I di intensità nota nella cellula e
si misura la conseguente variazione del potenziale di
membrana Vm
Quindi, ad ogni valore della corrente iniettata possiamo
associare un determinato valore di Vm
Riportiamo in un grafico i valori ottenuti:
6
6
5
5
Corrente (nA)
Corrente (nA)
Riportiamo adesso sullo stesso grafico altri valori ottenuti da un’altra cellula:
4
3
4
3
2
2
1
1
-70
-60
-50
-40
-30
-20
-10
0
10
Pot. di Membrana (mV)
La relazione
corrente/voltaggio è
lineare, come c’è da
aspettarsi se vale la legge
di Ohm: I=g·Vm
dove g = costante
Qual è la
differenza?
-70
-68
-66
-64
-62
-60
Pot. di Membrana (mV)
In questo caso la relazione
corrente/voltaggio non è
lineare, quindi non vale la
legge di Ohm: I=g·Vm
cioè g ≠ costante
Alcuni tipi di canali Ionici sono sempre aperti, altri no!
extracell.
intracell.
Sempre
aperti
Il loro comportamento è
ohmico: la relazione I/V è
lineare  g=costante
Voltaggio-dipendenti:
rispondono a
variazioni di Vm
Il loro comportamento non
è ohmico: la relazione I/V
non è lineare perché g
non è costante [g=f(Vm)]
Riassumendo
Se sulla membrana esistono canali voltaggio-dipendenti, le
variazioni del potenziale di membrana Vm in risposta ad uno stimolo
elettrico dipendono:
 oltre che dal tempo necessario a caricare la membrana, che si
comporta come un condensatore (proprietà passive di membrana),
 anche dal fatto che gm varia al variare del voltaggio e del tempo,
gm=f(V,t) (proprietà attive dei canali).
Il metodo di indagine del current-clamp non permette di separare la
componente resistiva della corrente (IR), dovuta alla presenza di
canali ionici, da quella capacitiva (IC), dovuta al comportamento
della membrana come un condensatore
La derivazione delle correnti ioniche transmembranarie
amplificatore
Neurone piramidale con un elettrodo di vetro attaccato per la derivazione delle correnti
ioniche transmembranarie mediante la tecnica del (patch-) voltage-clamp
La tecnica del voltage-clamp consiste nel bloccare il potenziale di membrana
ad un valore costante nel tempo e nel registrare le correnti ioniche
transmembranarie generate a tale potenziale di membrana
Potenziale di membrana
finale (Vm) costante
(mV)
20
Potenziale di riposo (Vr)
-70
0
10
20
Tempo (ms)
30
40
Corrente ionica (nA)
60
Corrente transmembranaria
generata dal passaggio di
Vm da –70 mV a +20 mV
40
20
0
-20
-40
-60
0
10
20
30
40
Tempo (ms)
Vantaggi del voltage-clamp:
In genere, gm = f(V,t) ma,
1.
Vm è bloccato ad un valore costante  gm = f(t) soltanto e può essere dedotto dall’andamento
della corrente ionica Ii
2.
E’ possibile separare Ii da Ic. Infatti cm è caricata istantaneamente
Voltaggio (mV)
Separazione farmacologica delle correnti IK e INa
20
-70
0
10
20
Tempo (ms)
30
40
+ TTX (IK)
INa+IK
Corrente ionica (nA)
60
40
20
0
+ TEA (INa)
-20
-40
-60
0
10
20
Tempo (ms)
30
40
Voltaggio-dipendenza dei canali Kv
140
120
100
+
I(K ) max (nA)
Voltaggio (mV)
60
50
40
30
20
10
0
-10
-20
-30
80
60
40
IK=gK• (V-EK)
20
0
-70
0
10
20
30
-20
40
-30 -20 -10 0
Tempo (ms)
10 20 30 40 50 60
Voltaggio (mV)
140
1.0
120
Conduttanza (μS)
Corrente K + (nA)
100
80
60
40
0.8
0.6
0.4
gK = IK/(V-EK)
20
0.2
0
0.0
-20
0
10
20
Tempo (ms)
30
40
EK=-80 mV
-30 -20 -10 0
10 20 30 40 50 60
Voltaggio (mV)
Quesito del giorno
Un ricercatore, in seguito ad esperimenti condotti in voltageclamp ha ricavato che la corrente di K+ (IK) dipende dal potenziale
di membrana (V) secondo la seguente relazione:
1


IK  4.6  (V  85)   1 
(V 10) / 9 
 1 e

(pA)
1) Calcolare i valori di IK nell’intervallo di potenziali tra –80 e
+80 mV ad intervalli di 10 mV e metterli in grafico in funzione di
V;
2) Dai valori di IK ricavati, e sapendo che EK= -85 mV, calcolare i
valori corrispondenti di gK e metterli in grafico in funzione di V;
3) A quale valore di V sara’ aperta la meta’ dei canali?
IK = 4.6·[1-1/(1+EXP((V+10/9))]·(V+85)
(pA)
EK = -85 mV
IK
0.0
0.1
0.4
1.9
7.1
24.7
74.1
172.5
294.2
394.3
466.4
522.9
572.8
620.2
666.7
712.9
759.0
Vm -EK
5
15
25
35
45
55
65
75
85
95
105
115
125
135
145
155
165
gK
0.002
0.006
0.018
0.053
0.158
0.450
1.139
2.300
3.461
4.150
4.442
4.547
4.582
4.594
4.598
4.599
4.600
600
400
200
0
-100
-50
0
50
100
mV
nS
Vm
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
pA
800
5.0
4.0
3.0
2.0
1.0
0.0
-100
-50
0
mV
50
100
Voltaggio-dipendenza dei canali Na
1
0
40
30
20
10
0
-10
-20
-30
-40
-50
-1
I(Na) picco (nA)
Voltaggio (mV)
60
-2
-3
-4
-6
-70
-7
0
10
20
30
40
-50 -40 -30 -20 -10 0 10 20 30 40
0
-1
-2
-3
-4
-5
0.12
gNa = INa/(VENa)
0.10
ENa=+50 mV
0.14
0
10
20
Tempo (ms)
30
40
0.08
0.06
0.04
0.02
0.00
-50 -40 -30 -20 -10 0 10 20 30 40
0
10
20
Tempo (ms)
60
Voltaggio (mV)
Conduttanza (μS)
I(Na) (nA)
I(Na) (nA)
Tempo (ms)
0
-1
-2
-3
-4
-5
-6
-7
INa=gNa• (V-ENa)
-5
30
40
Voltaggio (mV)
A parità di conduttanza, è la driving force che
determina l'andamento della relazione I/V
EA =+55mV
Vm
-80
-60
-40
-20
0
20
40
60
80
g (nS)
0.00
0.04
0.89
4.71
5.56
5.60
5.60
5.60
5.60
Vm -EA
-135
-115
-95
-75
-55
-35
-15
5
25
EB=-80mV
IA (pA)
-0.2
-4.3
-84.5
-353.3
-305.9
-196.0
-84.0
28.0
140.0
Vm -EB
5
25
45
65
85
105
125
145
165
1000
800
EA=+55mV
EB=-80mV
Corrente (pA)
600
400
200
0
-200
-400
-100 -80 -60 -40 -20
0
20
Voltaggio (mV)
40
60
80 100
IB (pA)
0.0
0.9
40.0
306.2
472.8
587.9
700.0
812.0
924.0
Quesito del giorno
Un ricercatore, in seguito ad esperimenti condotti in voltageclamp e utilizzando la tossina di scorpione per bloccare
l’inattivazione, ha ricavato che la conduttanza del canale del
Na+ (gNa) dipende dal potenziale di membrana (V) secondo la
seguente relazione:
1


gNa  5.6   1 
(V  30) / 6  (nS)
 1 e

1) Calcolare i valori di gNa nell’intervallo di potenziali tra –
80 e +80 mV ad intervalli di 10 mV e metterli in grafico in
funzione di V;
2) Dai valori di gNa ricavati, e sapendo che ENa= +55 mV,
calcolare i valori corrispondenti di INa e metterli in grafico in
funzione di V.
(nS)
ENa=+55 mV
nS
gNa=5.6(1-1/[1+EXP((V+30)/6)])
6.0
5.0
4.0
gNa (nS)
0.00
0.01
0.04
0.19
0.89
2.80
4.71
5.41
5.56
5.59
5.60
5.60
5.60
5.60
5.60
5.60
5.60
Vm -ENa
-135
-125
-115
-105
-95
-85
-75
-65
-55
-45
-35
-25
-15
-5
5
15
25
INa (pA)
-0.2
-0.9
-4.3
-20.3
-84.5
-238.0
-353.3
-351.5
-305.9
-251.7
-196.0
-140.0
-84.0
-28.0
28.0
84.0
140.0
3.0
2.0
1.0
0.0
-100
-50
0
50
100
50
100
mV
pA
Vm
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
200
100
0
-100
-50
-100
0
-200
-300
-400
mV
Canali voltaggio-dipendenti
- CINETICA Il movimento termico fa oscillare la proteina-canale
tra la conformazione aperta e quella chiusa
Quindi, questa transizione
Chiuso  Aperto
è un evento casuale
La legge delle probabilità ci permette
tuttavia di fare certe predizioni sul
comportamento medio del canale
Come esempio consideriamo un canale che ha
soltanto uno stato chiuso e uno stato aperto.
a
Closed
b
u.d.m: s-1
Open
Calcolo della Probabilità di apertura (Po)
dPO/dt = aPC – bPO
PO + PC = 1

dPC/dt = bPO - aPC
PC = 1 - PO
dPO/dt = a – aPO – bPO  dPO/dt = a – (a + b)PO
Risolvendo l’equazione differenziale e ponendo PO(t)=n(t),
si ottiene:
n(t) = a/(a  b)a/(a  b)exp[(a  b)t]a0/(a0  b0)exp[(a  b)t]
In particolare, all'equilibrio:
dPO/dt = a - (a  b)PO = 0

PO eq = a/(a  b) = n
Ponendo inoltre
a0/(a0  b0) = n0
e
1/(a  b) = t
si ottiene:
n(t) = n - (n - n0) exp(t/t)
Essa rappresenta la relazione tra le costanti di velocità e,
• a livello microscopico: la probabilità che un singolo canale
con un’unica gate sia aperto,
• a livello macroscopico: la frazione di canali (unica gate) aperti
60
-70
160
140
120
100
80
60
40
20
0
-20
Prob. di apertura (Po)
I(K)
Voltaggio (mV)
Cinetica delle correnti di K+ del canale Kv
1.0
0
10
20
Tempo (ms)
30
40
Ipotesi: una sola gate
Po=n(t)=n∞-(n∞-n0)∙exp(-t/τ)
I=g∙(V-E) ; gPo  I(t)n(t)∙(V-E)
I=g∙(V-E) ; gPo=n4
0
10
20
Tempo (ms)
30

I(t)n4(t)∙(V-E)
chiuso
aperto
-70mV
+60mV
40
Ipotesi: quattro gates identiche
Po= n∙n∙n∙n = n4
n4(t)=[n∞-(n∞-n0)∙exp(-t/τ)]4
1 gate
0.8
4 gates
0.6
0.4
0.2
0.0
0
10
20
Tempo (ms)
30
40
chiuso
aperto
Volt. (mV)
Cinetica delle correnti di Na+ voltaggio-dipendenti
20
-70
0
10
20
30
40
Ipotesi: tre gates identiche
Po=m3(t)=[m∞-(m∞-m0)∙exp(-t/τ)]3
Tempo (ms)
0
I(Na)
-5
-10
-15
Chiuso
Aperto
-70mV
+20mV
-20
-25
0
10
20
30
40
Prob. di apertura (Po)
Tempo (ms)
m(t)
1.0
Ipotesi:
tre gates identiche di attivazione
+
una gate di inattivazione
Po=m3(t)∙h(t)
h(t)
0.8
m3(t)
0.6
0.4
0.2
m3*h
0.0
0
10
20
Tempo (ms)
30
40
Chiuso
Aperto
Inattivato
-70mV
+20mV
+20mV
Quesito del giorno
Depolarizzando un neurone dal potenziale di riposo Vo ad un certo
potenziale Vf=+10 mV, la probabilita’ di apertura di una singola
gate di attivazione “n” del canale del K+ varia nel tempo seguendo
la seguente relazione temporale:
n(t) = 0.8·[1- EXP(-t / 1.1) ], dove il tempo t e’ espresso in ms.
Sapendo che quel tipo di canale del K+ ha 4 gates “n” identiche e
che la conduttanza massima GK e’ 25 nS:
1. calcolare e mettere in grafico i valori della conduttanza gK(t) ad
intervalli di 1 ms per una durata totale di 12 ms;
2. calcolare il valore di IK allo stato stazionario (EK = -80 mV).
n(t) = 0.8·[1- EXP(-t / 1.1) ]
EK=-80 mV GK=25 mS
g=G·n4
IK= g·(V-EK) = G·n4·(V-EK)
t(ms)
0
1
2
3
4
5
6
7
8
9
10
11
12
n
0.000
0.478
0.670
0.748
0.779
0.792
0.797
0.799
0.799
0.800
0.800
0.800
0.800
4
n
0.000
0.052
0.202
0.313
0.368
0.392
0.403
0.407
0.408
0.409
0.409
0.410
0.410
g (nS)
0.00
1.30
5.04
7.81
9.20
9.81
10.07
10.17
10.21
10.23
10.24
10.24
10.24
IK (pA)
0.0
117.2
453.8
703.2
828.2
883.1
905.9
915.3
919.0
920.6
921.2
921.4
921.5
12
10
8
6
4
2
0
0
2
4
6
8
10
12
14
Ancora un problema
Il potenziale di riposo di una cellula è determinato dalla presenza
di due canali permeabili rispettivamente agli ioni A e B attraverso
i quali passano le correnti IA e IB indicate in tabella.
Dopo aver disegnato i rispettivi grafici I/V, determinare:
1) le conduttanze gA e gB;
2) se i due canali sono voltaggio-dipendenti o -indipendenti;
3) il potenziale di equilibrio dei due ioni A e B;
4) il potenziale di riposo Vr della cellula.
V(mV)
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
IA (nA)
-1650
-1100
-550
0
550
1100
1650
2200
2750
3300
V(mV)
-20
-10
0
10
20
30
40
50
60
70
IB (nA)
-1320
-1100
-880
-660
-440
-220
0
220
440
660
V(mV)
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
IA =gA (V-EA ) (nA)
-1650
-1100
-550
0
550
1100
1650
2200
2750
3300
V(mV)
-20
-10
0
10
20
30
40
50
60
70
IB=gB(V-EB) (nA)
-1320
-1100
-880
-660
-440
-220
0
220
440
660
4000
3000
2000
EA
EB
1000
0
-150
-100
-50
0
-1000
-2000
EA=-90mV
g1A=I[(-120)-I(-110)]/[-120-(-110)]=
55
nS
EB=+40mV
g1B=I[(-20)-I(-10)]/[0-(-10)]=
22
nS
Vr=(EAgA+EBgB)/(gA+gB)= -52.9 mV
50
100
Confronto della voltaggio-dipendenza di gK e gNa
1.0
Conduttanza g
0.8
0.6
0.4
0.2
0.0
-60
-40
-20
0
Vm (mV)
20
40
60