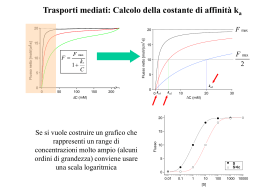
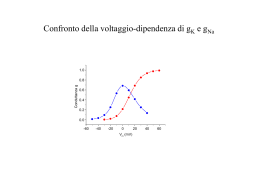
Studio della cinetica
delle correnti di Na e di K
voltaggio-dipendenti
Tempo-dipendenza del gating
Il modello della gate di H&H assume una reazione cinetica del 1o
ordine tra gli stati aperto e chiuso della particella di gating
a
C
O
b
Quindi, la probabilità della particella di trovarsi nello stato
aperto può essere descritta da:
(1-Po)
a
b
Po
Trattandosi di una cinetica del 1o ordine, sarà:
dPo
 a (1  Po )  bPo
dt
Allo stato stazionario (equilibrio) sarà:
a
quindi,
P 
o
ab
dPo
 a (1  Po )  bPo  0
dt
Risolvendo l’equazione differenziale del 1o ordine e applicando
la condizione al contorno Po0  Po(t  0), si ottiene:


Po(t )  Po0  (Po  Po0 ) 1  e (a  b )t

che si può anche scrivere così:
Po( t )  Po  ( Po  Po0 )e ( a  b )t
oppure così:
Po( t )  Po  ( Po0  Po )e ( a  b )t
1/(ab)=t rappresenta la costante di tempo dell’attivazione ed è
un indice della velocità di attivazione della particella di gating.
Se p particelle di gating indipendenti
sono coinvolte nel gating del canale,
allora il canale seguirà il seguente
andamento temporale: Pochann (t )  Po(t )p
Prob. Di Attivaz.
1.0
Po(t)
0.8
0.6
[Po(t)]p
0.4
0.2
0.0
0
2
4
Tempo
6
8
60
-70
160
140
120
100
80
60
40
20
0
-20
Prob. di apertura (Po)
I(K)
Voltaggio (mV)
Cinetica delle correnti di K+ del canale Kv
1.0
0
10
20
Tempo (ms)
30
40
Ipotesi: una sola gate
Po=n(t)=n∞-(n∞-n0)∙exp(-t/τ)
I=g∙(V-E) ; gPo I(t)n(t)∙(V-E)
I=g∙(V-E) ; gPo=n4  I(t)n4(t)∙(V-E)
0
10
20
Tempo (ms)
30
chiuso
aperto
-70mV
+60mV
40
Ipotesi: quattro gates identiche
Po= n∙n∙n∙n = n4
n4(t)=[n∞-(n∞-n0)∙exp(-t/τ)]4
1 gate
0.8
4 gates
0.6
0.4
0.2
0.0
0
10
20
Tempo (ms)
30
40
chiuso
aperto
Corrente (pA)
g (nS)
Gmax=4.5 nS
g=n(t)*Gmax
tempo (ms)
tempo (ms)
[n(t)]
2
g (nS)
4
Ipotesi: due gates
Po=[n(t)]2
3
Gmax=4.5 nS
2
g=[n(t)]2*Gmax
1
0
4
6
tempo (ms)
g (nS)
3
[n(t)]
Po=[n(t)]3
3
Gmax=4.5 nS
2
g=[n(t)]3*Gmax
1
2
4
6
100
2
4
6
Gmax=4.5 nS
2
g=[n(t)]4*Gmax
C orrente (pA)
3
1
500
400
I=g*(V-EK)
300
200
100
2
4
6
tempo (ms)
0
2
4
6
tempo (ms)
8
I=g*(V-EK)
0
tempo (ms)
8
600
0
tempo (ms)
g (nS)
4
[n(t)]
200
tempo (ms)
8
4
Po=[n(t)]4
I=g*(V-EK)
300
0
0
tempo (ms)
Ipotesi: quattro gates
400
0
0
5
500
8
Corrente (pA)
2
5
4
Ipotesi: tre gates
600
0
0
tempo (ms)
I=g*(V-EK)
tempo (ms)
5
Corren te (pA)
n(t)
Ipotesi: una sola gate
Po=n(t)
=n∞-(n∞-n0)∙exp(-t/t)
8
tempo (ms)
Volt. (mV)
Cinetica delle correnti di Na+ voltaggio-dipendenti
20
Vedi esempio di analisi
-70
0
10
20
30
40
Ipotesi: tre gates identiche
Po=m3(t)=[m∞-(m∞-m0)∙exp(-t/τ)]3
Tempo (ms)
0
I(Na)
-5
-10
-15
Chiuso
Aperto
-70mV
+20mV
-20
-25
0
10
20
30
40
Prob. di apertura (Po)
Tempo (ms)
m(t)
1.0
Ipotesi:
tre gates identiche di attivazione
+
una gate di inattivazione
Po=m3(t)∙h(t)
h(t)
0.8
m3(t)
0.6
0.4
0.2
m3*h
0.0
0
10
20
Tempo (ms)
30
40
Chiuso
Aperto
Inattivato
-70mV
+20mV
+20mV
Confronto della voltaggio-dipendenza di gK e gNa allo
stato stazionario e della loro tempo-dipendenza
(mV)
20
1.0
-70
0.6
0.4
0.2
0.0
-60
0
10
0
10
20
Tempo (ms)
30
40
30
40
60
-40
-20
0
Vm (mV)
20
40
60
Corrente ionica (nA)
Conduttanza g
0.8
40
20
0
-20
-40
-60
20
Tempo (ms)
Quesito del giorno
Depolarizzando un neurone dal potenziale di riposo Vo ad un certo
potenziale Vf=+10 mV, la probabilita’ di apertura di una singola
gate di attivazione “n” del canale del K+ varia nel tempo seguendo
la seguente relazione temporale:
n(t) = 0.8·[1- EXP(-t / 1.1) ], dove il tempo t e’ espresso in ms.
Sapendo che quel tipo di canale del K+ ha 4 gates “n” identiche e
che la conduttanza massima GK e’ 25 nS:
1. calcolare e mettere in grafico i valori della conduttanza gK(t) ad
intervalli di 1 ms per una durata totale di 12 ms;
2. calcolare il valore di IK allo stato stazionario (EK = -80 mV).
n(t) = 0.8·[1- EXP(-t / 1.1) ]
EK=-80 mV GK=25 mS
g=G·n4
IK= g·(V-EK) = G·n4·(V-EK)
t(ms)
0
1
2
3
4
5
6
7
8
9
10
11
12
n
0.000
0.478
0.670
0.748
0.779
0.792
0.797
0.799
0.799
0.800
0.800
0.800
0.800
4
n
0.000
0.052
0.202
0.313
0.368
0.392
0.403
0.407
0.408
0.409
0.409
0.410
0.410
g (nS)
0.00
1.30
5.04
7.81
9.20
9.81
10.07
10.17
10.21
10.23
10.24
10.24
10.24
IK (pA)
0.0
117.2
453.8
703.2
828.2
883.1
905.9
915.3
919.0
920.6
921.2
921.4
921.5
12
10
8
6
4
2
0
0
2
4
6
8
10
12
14
Caratterizzazione dei canali
Voltage clamp
É necessario clampare l’intera cellula altrimenti…
Blocco dei canali
La Tetrodotossina funziona bene per I canali del Na
Il tetraetilammonio funziona bene per I canali Kv
Applicazione di serie di potenziali
Si ottiene t, m se il canale è non-inattivante
Prepulsi per ottenere la cinetica di inattivazione
Canali ionici voltaggio-dipententi:
formulazione di HH
g = gmax . mx . hy
gmax è la conduttanza quando tutti i canali
sono aperti
m,h sono le probabilità delle singole
gates di trovarsi nello stato aperto
x, y sono il numero di gates
gNa = gNamax.m3h
gK = gKmax.n4
Formulazione di HH:
Canale del Na
Due processi: m e h
Chiuso
am
bm
Aperto
bh
ah
Inattivo
Se il canale rimane aperto troppo a
lungo diventa inattivo
Formulazioni di am, bm vs tm, m
Chiuso
1-m
a
b
Aperto
m
a, b sono funzioni di V
a, b  m , tm
Allo stato-stazionario,
Aperto/Chiuso = a/b (costante di equilibrio)
Ad ogni istante: Fraz. aperta = aperti/totale = m(t)
Allo stato-stazionario:
Vedi esempio di
Aperti/totale = m = a / a  b
calcolo di tm
tm = 1/(a  b)
a=m∞/tm b=(1-m∞)/tm
Formulazioni di am, bm vs tm, m
a
b
Chiuso
1-m
t (msec)
6
m
1
Aperto
m
0
0
-40
V (mV)
V (mV)
120
V (mV)
120
0.3
a(1/msec)
b(1/msec)
1.2
0
-40
120
0
-40
V (mV)
120
-40
Formulazioni di ah, bh vs th, h
Inattivo
1-h
a
b
Aperto
h
a, b sono funzioni di V
a, b  h , th
Allo stato-stazionario,
Aperto/Inattivo = a/b
Ad ogni istante: Fraz. aperta = aperti/totale = h(t)
Allo stato-stazionario:
Aperti/totale = h = a / a  b
Vedi esempio di
th = 1/(a  b)
calcolo di th
a=h∞/th b=(1-h∞)/th
Il potenziale d’azione
Na
Na+K
Corrente
Ra/2
Ra/2
Cm
Rm
Vm
Carica
GK
GNa
EK
ENa
Tutti chiusi
K
I Na
IK
I leak
stimolo
dV
 GNa m 3 h(V  E Na )  GK n 4 (V  E K )  Gl (V  El )  I (t )
C
dt
m  m0 (V)
h  h0 (V)
n  n0 (V)
dm
dh
dn



t m (V)
t h (V)
t n (V)
dt
dt
dt
Genesi ionica del potenziale d’azione
ancor più canali del
sodio si aprono
i canali del sodio
inattivano
si aprono i
canali del sodio
si aprono i canali
del potassio
i canali del potassio
si chiudono
tempo
Vm
ENa= +47 mV
EK= -86 mV
time (ms)
0.9
Vm (mV)
gNa (S)
Vm -ENa
INa (A) = gNa(Vm -ENa)
gK
Vm -EK
IK (A) = gK(Vm -EK)
Vm =(INa+IK+gNa*ENa+gK*EK)/(gNa+gK)
-58
0.2
-105
-21
0
28
0
-58
Evento eccitatorio (cariche (+)
entrano nella cellula)
La Depolarizzazione è sentita
da una piccola percentuale di
canali Na+ che si aprono e
permettono al Na+ (cariche +)
che entra di causare
un’ulteriore depolarizzazione
della membrana
0.9
Feedback positivo
Depolarizz
.
piu’ canali Na+
si aprono
più cariche +
entrano
Vm
time (ms)
1.9
Vm (mV)
gNa (S)
Vm -ENa
INa (A) = gNa(Vm -ENa)
gK
Vm -EK
IK (A) = gK(Vm -EK)
Vm =(INa+IK+gNa*ENa+gK*EK)/(gNa+gK)
20
15.0
-27
-411
1
106
106
20
La depolarizzazione è sentita
da ancor più canali Na+ che
pure si aprono e permettono a
più ioni Na+ (più cariche +) di
entrare, causando un’ulteriore
depolarizzazione della
membrana
1.9
Feedback positivo
Depolarizz
.
piu’ canali Na+
si aprono
più cariche +
entrano
Vm
ENa= +47 mV
time (ms)
2.1
Vm (mV)
gNa (S)
Vm -ENa
INa (A) = gNa(Vm -ENa)
gK
Vm -EK
IK (A) = gK(Vm -EK)
Vm =(INa+IK+gNa*ENa+gK*EK)/(gNa+gK)
38
28.0
-10
-266
1.5
124
185
38
Grazie ai canali Na+ aperti il
potenziale di membrana sta
raggiungendo ENa
2.1
Vm
time (ms)
2.9
Vm (mV)
gNa (S)
Vm -ENa
INa (A) = gNa(Vm -ENa)
gK
Vm -EK
IK (A) = gK(Vm -EK)
Vm =(INa+IK+gNa*ENa+gK*EK)/(gNa+gK)
-9
14.0
-56
-789.32
10.9
77
835
-9
I canali Na+ rimangono aperti
solo per un breve periodo e a
questo punto tendono a chiudersi
(inattivazione)
A questo punto una certa frazione
di canali K+ ha incominciato ad
aprirsi permettendo alle cariche
(+) di fuoriuscire
2.9
Vm
Tutti i canali Na+ sono inattivati
I canali K+ riportano il potenziale di membtana
verso EK, dopo di che alcuni canali K+ si
chiudono e Vm si stabilizza
time (ms)
7
Vm (mV)
gNa (S)
Vm -ENa
INa (A) = gNa(Vm -ENa)
gK
Vm -EK
IK (A) = gK(Vm -EK)
Vm =(INa+IK+gNa*ENa+gK*EK)/(gNa+gK)
-80
0
-127
0
3.1
6
19
-80
7.
0
Feedback negativo
Depolarizz
-
.
Piu’ canali K+
si aprono
(ripolarizzaz.)
Più cariche +
escono
Caratteristiche generali del potenziale d’azione
La soglia
Lo stimolo soglia è lo stimolo depolarizzante di intensità minima in
grado di generare un potenziale d’azione in un neurone
La legge del tutto o nulla
In un neurone un potenziale d’azione o è generaro e si sviluppa in tutta
la sua ampiezza, se lo stimolo raggiunge o supera la soglia, oppure non è
generato affatto, se l’ampezza dello stimolo è inferiore alla soglia.
La refrattarietà
Un neurone, una volta generato un potenziale d’azione viene a trovarsi
in uno stato di refrattarietà
- periodo di refrattarietà assoluta: nessuno stimolo per quanto
intenso è in grado di genrare un secondo potenziale d’azione
- periodo di refrattarietà relativa: un secondo stimolo, a condizione
che sia sufficientemente più intenso di quello soglia, è in grado di
genrare un secondo potenziale d’azione
Soglia
Legge del tutto o nulla
Refrattarietà
con
HHsim
http://www.cs.cmu.edu/~dst/HHsim/