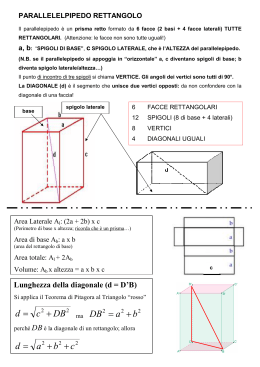
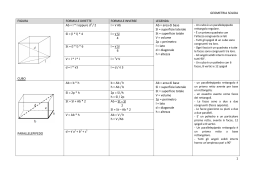
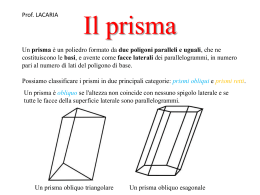
La 1° definizione è la seguente: Un poliedro è un solido limitato da più
poligoni posti in piani diversi e tali che ogni lato è comune a due soli di
essi.
Poliedri regolari
Un poliedro si dice regolare se tutte le sue facce sono poligoni regolari
congruenti fra loro.
Un esempio di poliedro regolare è l’esaedro regolare o
cubo
Un esempio di poliedro non regolare è il prisma
base
Le basi: facce
congruenti e parallele
altezza
Spigolo laterale
Faccia laterale
Facce laterali:
poligoni che
delimitano
lateralmente il
poliedro
Altezza: distanza fra
le due basi
Spigoli laterali: lati
delle facce laterali
base
Spigolo di base
Spigoli di base: lati
delle basi
Un prisma si dice retto se ha tutte le facce
laterali perpendicolari alle basi.
Se è retto e ha per base un poligono regolare
si dice regolare.
Prisma regolare a
base esagonale
Prima di procedere nel calcolo delle
superfici e del volume, per
comprendere i procedimenti di calcolo
rappresentiamo lo sviluppo sul piano
del precedente prisma.
Possiamo dedurre che:
La superficie laterale del prisma coincide con
la superficie del rettangolo ABCD dello
sviluppo: questo rettangolo ha la base
congruente al perimetro di base del prisma e
l’altezza congruente all’altezza del prisma.
D
A
L’area della superficie laterale è
SL
SL = perimetro di base (2p) x altezza (h)
(Formula diretta)
h
B
2p
2p 
Sl
h
h
Sl
2p
C
(formule inverse)
Dal disegno è evidente che per ottenere la superficie totale, non dobbiamo
fare altro che aggiungere l’area delle due basi alla superficie laterale (Sl).
Tradotto nel linguaggio matematico:
D
A
SL
St  Sl  2 Ab
( formula diretta)
B
base
h
2p
St  Sl
Sl  St  2 Ab
Ab 
2
( formule inverse)
C
Calcolare il volume di un prisma vuol dire verificare quante volte l’unità di
misura del volume, per esempio il cm³, è contenuta nel solido.
Consideriamo, allora, un prisma retto a base quadrata con il lato lungo 3 cm e
l’altezza 4 cm. Scomponiamolo in tanti cubi unitari aventi lo spigolo 1 cm:
quanti di questi cubi sono contenuti nel nostro prisma?
Se osserviamo la figura il prisma è stato scomposto
in 4 strati di (3x3) cubi ciascuno, cioè 36 cubi, per
cui il volume è di 36 cm³.
Otteniamo lo stesso risultato se moltiplichiamo
l’area della base per la misura dell’altezza.
In formula avremo:
V  Ab  h ( formula diretta)
V
V
Ab 
h
( formule inverse)
h
Ab