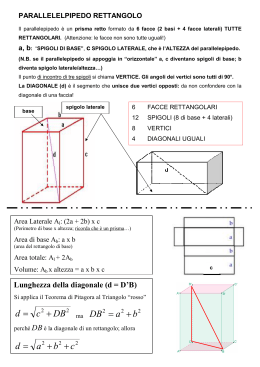
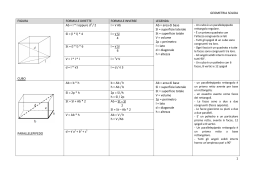
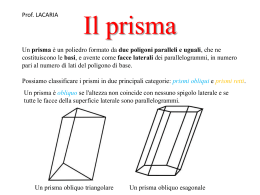
I PRISMI
Def:
si dice PRISMA un poliedro limitato da due POLIGONI posti su piani paralleli e con
i lati rispettivamente paralleli, e da tanti PARALLELOGRAMMI quanti sono i lati
del poligono di base.
In un prisma si ha:
 BASI, su piani paralleli (
)
 FACCE LATERALI, sono i parallelogrammi
(ABB’A’, ACC’A’, BCC’B’)
 SPIGOLI DI BASE, lati del poligono di base
(
)
 SPIGOLI LATERALI, i lati di tutti i
parallelogrammi laterali (
)
 ALTEZZA, distanza tra i due piani paralleli che contengono le basi
 SUPERFICIE LATERALE, somma delle aree di tutti i parallelogrammi
laterali
 SUPERFICIE TOTALE, superficie laterale sommata alle aree dei poligoni di
base
 VOLUME, spazio contenuto dentro al prisma.
Def:
Un prisma si dice RETTO, se gli spigoli laterali sono perpendicolari agli spigoli di
base:
 Le facce laterali sono RETTANGOLI
 L’ALTEZZA coincide con gli SPIGOLI
LATERALI
1
Def:
Un prisma si dice OBLIQUO, se gli spigoli laterali NON sono perpendicolari alle
basi:
 Le facce laterali sono PARALLELOGRAMMI
 B’H è altezza
Def:
un prisma si dice REGOLARE se è RETTO e se le basi sono dei POLIGONI
REGOLARI:
 Le facce laterali sono tutti RETTANGOLI CONGRUENTI
AREA DELLA SUPERFICIE DI UN PRISMA RETTO
Def:
la SUPERFICIE LATERALE di un PRISMA RETTO si ottiene moltiplicando il
perimetro di base per l’altezza del prisma.
Dimostrazione:
Se tagliamo il prisma lungo uno spigolo otteniamo lo sviluppo piano del prisma,
escluse le basi:
è un rettangolo che ha per base il PERIMETRO DI BASE,
e per altezza ha l’ALTEZZA DEL PRISMA.
Allora l’area del rettangolo è l’area laterale del prisma:

2
= area laterale
= perimetro di base
Def:
la SUPERFICIE TOTALE di un PRISMA RETTO si ottiene sommando l’area
laterale alle due aree di base:
AREA LATERALE
AREA TOTALE
AREA BASE
FORMULE INVERSE
3