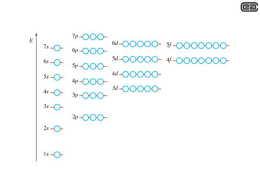
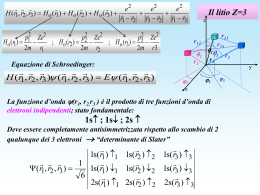
2p+
2s
1s
2po
Il carbonio (Z=6)
2p-
configurazione
elettronica del C
nello stato
fondamentale di
tripletto di spin
- 2 elettroni “equivalenti” nello stato 2p
- la funzione d’onda globale deve essere antisimmetrica

[He] (2s)2 (2p)2
1
 (5,6)  (6,5)
2
tripletto di
spin, S=1
2 possibilità:
2p+
2s
1s
2po
2p-
configurazione
elettronica del C
nello stato
eccitato di
singoletto di spin
[He] (2s)2 (2p)2
=
parte spaziale
antisimmetrica
parte di spin
simmetrica
=
parte spaziale
simmetrica
parte di spin
antisimmetrica
regola di Hund:
il tripletto ha energia minore
singoletto di
spin, S=0
Il momento angolare totale del carbonio
2p+
2po
2p-
2s
configurazione
elettronica del C
nello stato
fondamentale di
tripletto di spin
1s
[He] (2s)2 (2p)2
un nuovo problema:
come comporre i momenti angolari
orbitali in modo da avere una funzione
d’onda con la corretta simmetria o
antisimmetria spaziale?
3 possibili valori:
   

L5,6  l5  l6  1  1
2p+
2po
2p-
configurazione
2s
elettronica del C
nello stato
eccitato di
singoletto di spin
1s
[He] (2s)2 (2p)2
L=2  stato D
L=1  stato P
L=0  stato S
P è antisimmetrico
tripletto, S=1 3P
stato fondamentale
EP =-11,3 eV
S e D sono simmetrici
singoletto, S=0 1D, 1S
stati eccitati
ED =-10,1 eV ; ES = -8,7 eV
Uno stato eccitato interessante
2p+
2s
1s
2po
2p-
configurazione
elettronica del C
nello stato
eccitato con S=2
[He] (2s) (2p)3
la grafite è C allo
stato solido, con
legame ibrido
sp2
il diamante è C allo
stato solido, con
legame ibrido sp3
-uno stato eccitato molto interessante del
carbonio è lo stato con S=2
- favorito in energia per la regola di Hund
- 3 elettroni “equivalenti” nello stato 2p, 1
solo elettrone nello stato 2s
- il carbonio si comporta come tetravente
- energia di legame = -7 eV
- è uno stato metastabile nell’atomo isolato
- è alla base dei legami ibridi del carbonio
nello stato solido e nelle molecole organiche
la molecola
di benzene
Stato fondamentale e stati eccitati del carbonio
E
(eV)
2s2 2p 3s
1P
-3,7 eV
2s2 2p 2s
3P
- 3,9 eV
2s 2p3
5S
- 7 eV
2s22p2
1S
2s22p2
1D
-8,7 eV
-10 eV
2s22p2
3P
- 11,3 eV
S=0
S=1
S=2
Z
configurazione
simbolo stato fondamentale
energia di
ionizzazione (eV)
s
1
H
1s
13,6
K
2
He
(1s)2
24,6
K
3
Li
[He] 2s
5,4
L
K
4
Be
[He] (2s)2
9,3
5
B
[He] (2s)2 2p
8,3
L
K
C
[He] (2s)2 (2p)2
7
N
[He]
(2s)2 (2p)3
14,5
8
O
[He] (2s)2 (2p)4
13,6
9
F
[He]
(2s)2 (2p)5
17,4
10
Ne
[He] (2s)2 (2p)6
21,6
11,3
(1s)2 = [He]
Regole per il
riempimento degli
stati nei primi due
periodi:
L
K
6
p
Tabella
periodica
L
K
L
K
L
K
L
•principio di
esclusione
•stato con n minore
•a parità di n, stato
con l minore
•regola di Hund
•“gas nobile” al
riempimento della
shell
K
L
K
[He] (2s)2 (2p)6 = [Ne]
E
(eV)
H
Li
Na
0
4
-1
4s
4p
4d
0
Na
Z=11
4d
4p
3d
3d
3p
-3
Il sodio
-1
3
3s
-2
E
(eV)
4s
3p
2
- 1 solo
-2 elettrone fuori
della shell
chiusa del
-3
[Ne]
2p
-4
-4
atomo
“alcalino”
-bassa energia
di ionizzazione
E = -5,1 eV
-5
3s
-5
2s
-6
idrogeno - litio - sodio
-6
- livelli
energetici
simili a quelli
del Li
E
(eV)
splitting dei livelli del sodio
Perché la linea gialla
del sodio è sdoppiata?
0
E 10-6eV
-1
-2
4d5/2
4d3/2
E 7·10-4eV
4p3/2
3d5/2
4p1/2
E
4s1/2
6·10-5eV
3d3/2
Accoppiamento di spin-orbita:
il “buon numero quantico” è il
momento angolare totale j
dell’elettrone che può avere due
valori a parità di l:
j=l+1/2
j=l-1/2
-3
E 2·10-3eV
-4
-5
3s1/2
-6
3p3/2
Negli atomi,
3p1/2
- l’effetto sull’energia è piccolo
(accoppiamento magnetico fra il
momento magnetico di spin e il
campo magnetico visto
dall’elettrone in moto, per effetto
della trasformazione di Lorentz
del campo coulombiano)
- lo stato j=l-1/2 ha energia
minore
E
(eV)
principali transizioni radiative del sodio
0
E 10-6eV
-1
-2
-3
4d3/2
E
4p3/2
7·10-4eV
3d5/2
4p1/2
3d3/2
E 6·10-5eV
4s1/2
proibita
in dipolo
elettrico
3p3/2
E 2·10-3eV
3p1/2
-4
-5
3s1/2
-6
4d5/2
praticamente
coincidenti in
energia
linea “D”
doppietto giallo
del sodio
Regole di selezione
di dipolo elettrico:
l =1
 ml = 0,  1
 S= 0
 ms = 0
 j = 0,  1
Z
configurazione
simbolo stato fondamentale
energia di
ionizzazione (eV)
s
11
Na
[Ne] 3s
5,1
M
L
K
12
Mg
[Ne] (3s)2
7,6
M
L
K
13
Al
[Ne] (3s)2 3p
6,0
M
L
K
14
Si
[Ne] (3s)2 (3p)2
8,1
M
L
K
15
P
[Ne] (3s)2 (3p)3
10,5
M
L
K
16
S
[Ne] (3s)2 (3p)4
10,4
M
L
K
17
Cl
[Ne] (3s)2 (3p)5
13,0
M
L
K
18
Ar
[He] (3s)2 (3p)6
15,8
M
L
K
[Ar] 4s
4,3
N
M
L
K
19 K
p
d
Tabella
periodica
Regole per il
riempimento degli
stati:
•principio di
esclusione
•stato con n+l
minore
•a parità di n+ l,
stato con n
minore
•regola di Hund
• il “gas nobile”
al riempimento
dell’orbitale p
[Ne] (3s)2 (3p)6 = [Ar]
Z
configurazione
simbolo stato fondamentale
energia di
ionizzazione (eV)
s
19
K
[Ar] 4s
4,3
N
M
20
Ca
[Ar] (4s)2
6,1
N
M
21
Sc
[Ar] (4s)2 3d
6,5
N
M
22
Ti
[Ar] (4s)2 (3d)2
6,8
N
M
23
V
[Ar] (4s)2 (3d)3
6,7
N
M
6,8
N
M
7,4
N
M
4s (3d)5
24
Cr
[Ar]
25
Mn
[Ar] (4s)2 (3d)5
p
d
Tabella
periodica
Regole per il
riempimento degli
stati:
•principio di
esclusione
•stato con n+l
minore
26
Fe
[Ar] (4s)2 (3d)6
7,9
N
M
27
Co
[Ar] (4s)2 (3d)7
7,9
N
M
•a parità di n+ l,
stato con n
minore
28
Ni
[Ar] (4s)2 (3d)8
7,6
N
M
•regola di Hund
29
Cu
[Ar] 4s (3d)10
7,7
N
M
30
Zn
[Ar] (4s)2 (3d)10
9,4
N
M
•il “gas nobile”
al riempimento
dell’orbitale p
31
Ga
[Ar] (4s)2 (3d)10 4p
6,0
N
M
volumi atomici
energie di ionizzazione
.
n=3, l=2
n=4, l=2
n=5, l=2
n=6, l=2
n=4, l=3
n=5, l=3
Come leggere la tavola periodica
Esempio: il polonio (Po); Z=84
.
- ha il guscio interno
dello Xe, che
comprende la
configurazione
elettronica di 54
elettroni
-è nel gruppo
dell’O, 4 periodi
sotto:  (6p)4
- ha davanti 10 stati
dell’orbitale 5d: 
(5d)10
- davanti ancora 14
stati dell’orbitale 4f:
 (4f)14
-davanti ancora 2
stati dell’orbitale 6s:
 (6s)2
[Xe](6s)2(4f)14(5d)10(6p)4
E
(keV)
L edge
0
2
M
M edge
n

4-N
3-M
2-L
L L
4
K
K
K
8
K edge
6
Legge di Moseley:
f = A(Z-c)
con A2  11/h eV
10
12
Raggi X:
spettri di
emissione
di un
atomo con
Z 30
c1
1-K
sdoppiamenti di
“struttura fine”
4-N
V
IV
III
II
I
3-M
2-L
L
L
III
II
I
2d
5/2
2d
3/2
2p
3/2
2p
1/2
2s
1/2
2p
3/2
2p
1/2
2s
1/2
j=l+1/2
j=l-1/2
j=l+1/2
j=l-1/2
j=l+1/2
j=l-1/2
Raggi X:
struttura fine
degli spettri di
emissione di
un atomo con
Z 30
1-K
K
K K
4-N
V
IV
III
II
I
3-M
M
2-L
L
III
II
I
2d
5/2
2d
3/2
2p
3/2
2p
1/2
2s
1/2
2p
3/2
2p
1/2
2s
1/2
Raggi X: spettri
di assorbimento
di un atomo con
Z 30
1-K
K
Modello a shell nei nuclei
Energia
Accoppiamento di spin-orbita:
1d
2s
1p
1s
3/2
20
1/2
5/2
16
14
1/2
8
3/2
6
1/2
j
Ca20
il “buon numero quantico” è il
momento angolare totale j del
nucleone (protone o neutrone),
che può avere due valori a parità
di l:
j=l+1/2
j=l-1/2
O8
2
Nucleo
Z “magico”
Nei nuclei,
- l’effetto sull’energia è grande
- lo stato j=l-1/2 ha energia
maggiore