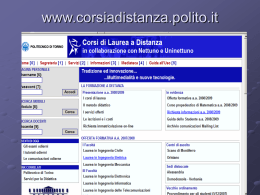
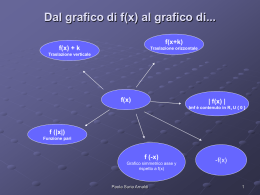
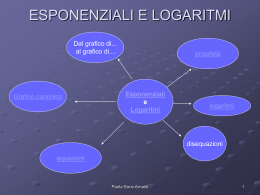
Formule di goniometria
2t
sin x 
1 t 2
1 t 2
cos x 
2
1 t
2t
tan x 
2
1 t
con
Paola Suria Arnaldi
x
t  tan
2
1
Equazioni lineari in seno e
coseno
a*sin x + b * cos x + c = 0
Metodi di risoluzione:
• Formule parametriche
• Cerchio e retta
Paola Suria Arnaldi
2
Qualche applicazione
Sin x + cos x = 1
2t
1 t 2
2
2


1
;

2
t

1

t

1

t
;
2
2
1 t
1 t
semplifico ed ottengo :
2 t  2 t 2  0  t (1  t )  0;
t  0 oppure
t 1
sostituisco t
ed ottengo
x
x
tg
 0 oppure
tg
 1;
2
2
x
1.
 k
 x  2 k
2
x


2.

 k  x 
 2 k
2
4
2
Paola Suria Arnaldi
3
Cerchio e retta
X Y  1
X  1Y
cos x  X
 2


2
2
2
sin
x

Y
X

Y

1
(
1

Y
)

Y
1



  
  

 2

2
2
1  2Y  Y  Y  1 2Y  2Y  0
  
Y  0
Y  1
 1.
2.

Y (Y  1)  0
X  1
X  0
1.x  0  2k
2.x   / 2  2k
Paola Suria Arnaldi
4
Equazioni omogenee in seno
e coseno
• I grado: a cos x +b sin x=0
• II grado a sin2x + b sinx * cos x +c cos2x +d=0
•I grado: divido per cos x e l’equazione diventa a + b tag x= 0
•II grado:
•Moltiplico d per 1 e cioè per (cos2x + sin2x=1 )
•divido per cos2x ed ottengo: a Tg 2x + b tg x + c + d(1+tg2x)=0
•Ottengo un’equazione di II grado in tangente di x
Paola Suria Arnaldi
5
Dall’equazione alla
disequazione
• La soluzione delle disequazioni può
essere fatta con metodo grafico
Paola Suria Arnaldi
6
Sin x > ½
Paola Suria Arnaldi
7