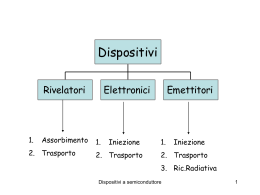
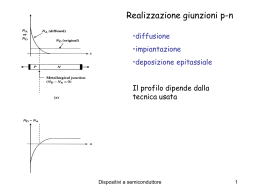
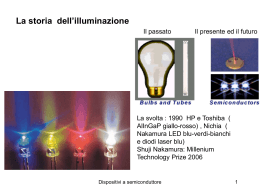
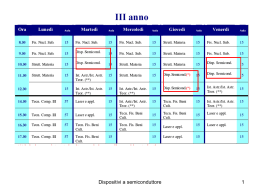
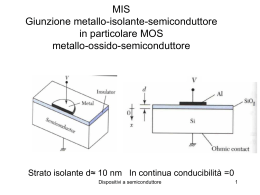
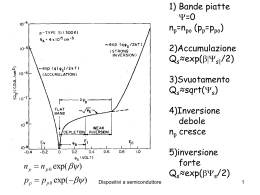
La diffusione
Esiste un gradiente di concentrazione dei
portatori n, p
( Giunzione, illuminazione non
uniforme,etc.)
Per convenzione il
flusso è >0 verso
destra
n(x-x)
n(x+x)
S
1
1
1 n(x)
(x)  v  n(x  x)  v  n(x  x)  
vx
6
6
3 x
Dispositivi a semiconduttore
1
x  v  
1
n(x)
(x)   v 2
3
x
3kB T
m*
k T n(x)
n(x)
(x)   B *
 D
m x
x
 v 2 
segue

J diff  D
n(x)
x
J diff  Dn
De(h ) 
I legge di Fick
kB T
 e(h )
*
m e(h )
kB T  e
kB T
De  *
e
e Rel. di Einstein
me e
e
k T
Dh  B h
e
Dispositivi a semiconduttore

2
Conservazione del numero di particelle
n
n
   Jdiff  0 segue

  D 2 n
t
t

II legge di
Fick:
equ.diffusione
Corrente totale JTOT  J Drift  J Diff
J e  nee E  eDen

J h  peh E  eDh p
Le correnti di drift hanno lo
stesso segno, mentre quelle
di diffusione hanno segno
opposto
Dispositivi a semiconduttore
3
La diffusione
Dispositivi a semiconduttore
4
Esprimiamo EF in funzione della concentrazione
intrinseca ni
Quasi livello di Fermi EF
Livello intrinseco di Fermi Ei
n  n ie
E F E i 


 kB T 
n
E F  E i  kB T ln
ni
Dispositivi a semiconduttore
5
Caso 1D
n
J x  en nE  eDe
x
dE F dE i
1 n

 kT
dx
dx
n x
en nE  eDe
n 
dn
dx
In condizioni di equilibrio:
De dn
D dn
D dn
 e
 ee
n (Edx) n (dV pot ) n dE F
n  N ce
n 
Se varia n varia EF: il livello
Ei cambia a causa della
presenza del campo E
E F E c 


 kB T 
eDe
kB T
Jx=0
Rel. Einstein
Dispositivi a semiconduttore
6
Come si misura la mobilità
In questa geometria
Effetto Hall
r
r
FL  qvD  B
Fy  qvD Bz
vD   E x
Fy  q E x Bz
qE y  q E x Bz
VHall  E y w    wE x Bz
Ey
1
RH 

J x Bz nq
Dispositivi a semiconduttore
7
Processi di generazione e ricombinazione
A differenza del caso del trasporto:
Interazione fra popolazioni e-h
• Transizioni interbanda : Assorbimento,
Emissione
Assorbimento:
h=Ee+Eh
Emissione radiativa: Ee’+Eh’= h
Emissione non radiativa
Dispositivi a semiconduttore
8
Regola aurea Fermi
| i ,| f 
W i f 
P(t) 2

| f | H if | i |2  (E f  E i  h )
t
h
Dispositivi a semiconduttore
9
Considerando transizioni ad 1 fotone
H
1
( p  eA) 2  V (r)
2m
r v
r v
1
i( k p  r t )
i( k p  r t )
ˆ
A(r,t)  Aoe(e
e
)
2
p2
e
H
 V (r)  A  p  H 0  H1
2m
m
W 
2
e
| ck'| A  p | vk |2  (E c (k')  E v (k)  h )
h
m
ck’:
stato b.cond.

con vettore k’
vk: stato b.val.
con vettore k
Dispositivi a semiconduttore
10
W cv 
e 2
2hm 2
v r
A02 | ck'| exp(ik p  r )eˆ  p | vk |2  (EC  E v  h )
r r
| jk  u jk (r)exp(ik  r )
eˆ  pcv 




1 ik' r *
ik r
e uck' (r)e p eˆ  pe ikr uvk (r)d 3 r

VV
1 i(k p k k' )r *
3
ˆ
e
u
(r)
e

(
p

hk)u
(r)d
r
ck'
vk

VV
Trasformando l’integrale sul volume sulla somma in
cui compare l’integrale su cella unitaria e
sfruttando le proprietà delle f.Bloch si ha:
eˆ  pcv 
 i(k p k k ' )r *
1 
'
exp(i(k

k

k
)

R
)
uck' (r)eˆ  ( p  hk)uvk (r)d 3 r

p
l  e

V  l

≠0 solo per kp+k-k’=Gm vettore ret.reciproco Gm=mG0
Dispositivi a semiconduttore
11
Kp<<Gm in particolare Kp<<G0 : contributo max per
Gm=0 quindi k’=k
conservazione impulso: transizione verticali o
Transizione diretta
e
i(k p k k ' )r *
ck'
u (r)eˆ  ( p  hk)uvk (r)d 3r

L’integrale su hk è 0 per ortogonalità f.Bloch

1
ˆe  pcv   u*ck' (r)(eˆ  p)uvk (r)d 3 r k,k'


Dispositivi a semiconduttore
12
A ordini superiori anche transizioni indirette:
fononi
Dispositivi a semiconduttore
13
Processi di rilassamento
•
•
•
•
•
•
Scale temporali : sub ps, ps, ns..
Perdita coerenza: sub ps, ps
Perdita energia : rilassamento intrabanda: ps
Perdita energia comporta anche termalizzazione
Ricombinazione interbanda radiativa e non: ns, ms
Anche processi estrinseci di cattura e
ricombinazione radiativa e non
Dispositivi a semiconduttore
14
Eccitone
Interazione
coulombiana e-h:
formazione di stati
legati di tipo
idrogenoide
h2 K X2
b 1
EX  Eg 
TOT  E X
2M X
n2
 1
E  13.6
2 eV
me  r
b
X
GaAs: EX=4meV: no
eccitoni @RT
GaN : EX=25meV:
eccitoni @RT
Dispositivi a semiconduttore
15
Risonanze eccitoniche
Assorbimento
GaN 77 K
Emissione
Dispositivi a semiconduttore
16
GaAs: effetto della
temperatura e
drogaggio
Dispositivi a semiconduttore
17
La coda di Urbach
Parametro Urbach legato a localizzazione-disordine
Dispositivi a semiconduttore
18
•Ricombinazione diretta,
•via trappole profonde (Shockley-Read-Hall)
•Processi Auger
•Ricombinazione da stati superficiali
Dispositivi a semiconduttore
19
Emissione assistita da fononi: repliche fononiche
Tipica in semiconduttori polari: necessaria “ forte” interazione con il
reticolo.
Dispositivi a semiconduttore
20
Attivazione termica di processi non radiativi
I(0)
IPL (T) 
 Ei


1   Ai exp 
T
k

B
i
Legge di Arrhenius: Ei i-sima energia di attivazione

Dispositivi a semiconduttore
21