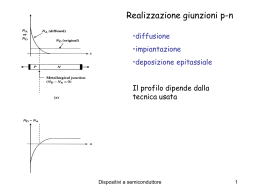
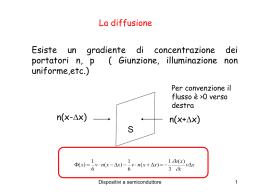
Popolamento delle bande
• Densità stati
• Distribuzione statistica e,h
• Hp: Distribuzione Termica
Dispositivi a semiconduttore
1
Distribuzione di Fermi
1

E   
1  exp 

KT


1

 E  EF 
1  exp 

KT


f (E) 
Dispositivi a semiconduttore
2
fe 
1
E  E 
F
1 exp

 k B T 
f h  1 f e  1
fh 
1
E e  E F 
1 exp

k
T
 B

1
E  E 
e
1 exp F

 k B T 
E h  E e
E Fh  E F
fh 
1
E h  E Fh 
1 exp

Dispositivi k
a semiconduttore
T
 B

3
Caso intrinseco
n

f e (E)  e (E )dE
BC
Caso3D  B.Isotrope
 e (E)  4  2m
n  4  2m
3
* 2
e

3
* 2
e

1
h3
E  Ec
1
 E  Ec
h 3 BC
dE
E  E F 
1 exp

k
T
 B 
Limite non degenere: (E-EF)>>KBT (≈4 KBT)

fe=exp(EF/KBT)exp(-E/KBT) : Distribuzione di Boltzmann

BC

E cmax

 
In virtù della distribuzione di Boltzmann
Dispositivi
E c a semiconduttore
Ec
4
(E  EC )
x
k BT
1
dx 
dE
k BT
 
n  4 2m
3
* 2
e
1
e
3
h
 E F  Ec 
 k T 
B
3 
2
kBT  
xe x dx
0
2
Nc2/sqrt
n  NC e
 E F  Ec 
 k T 

B
 2 me*

N C  2  2 k BT 
 h


NC≈1025/m3 nel Si @300K
3
2
Dispositivi a semiconduttore
5
Per le lacune:
p  NV e
E v E F 


 kB T 
Legge azione di massa:

np  NC NV e

Eg
kB T
n
2
i
NC, NV: densità effettive degli stati in banda conduzione e valenza
Dispositivi a semiconduttore
6
Dispositivi a semiconduttore
7
Caso intrinseco: dove sta l’energia di Fermi
n p
NC e
Caso bande isotrope
 EF  EC 
 k T 
B
 NV e
NV  m 

N C  m 
*
h
*
e
 EV  EF 
 k T 
B
N
EF  EC  k BT ln V  EV  EF
NC
1
kT N
EF  EC   Eg  B ln V
2
2
NC
3
2
1
k BT 3  mh* 
EF  EC   Eg 
g ln
2
2 2  me* 
1
T segue

 EF  Eg
2
ni  N C NV e
Dispositivi a semiconduttore
 Eg 


 2 kB T 
8
Dispositivi a semiconduttore
9
Semic. a gap crescente
Concentrazione intrinseca
portatori
in Si @ 300K ≈1010/cm3 contro una
concentrazione di atomi di
1022/cm3: ionizzazione 10-12
Dispositivi a semiconduttore
10
Caso estrinseco
Na: accettori
n  N a  p  N d
Neutralità:
Na
0
Na-
N d  N d
n  Nd
Nd0
Nd: donori
n  NC e
 EF  EC 
 k T 
B
 Nd
Nd+
Drogaggio n:
donori completamente ionizzati (OK @
RT): elettroni portatori maggioritari,
lacune portatori minoritari
Nd≈1014/cm3
NC≈1019/cm3
ni2
p
Nd
EF  EC  k BT ln
Nd
Nc
|EF-EC|≈10kBT= 250meV @300K
Dispositivi a semiconduttore
11
A partire da una certa temperatura conta anche ionizzazione intrinseca
Drogaggio p
Drogaggio n
n  N a  p  N d
n  p  Nd
N
p a 
2
np  p( p  N d )  ni2
N a2
 ni2
4
p 2  pN d  ni2  0
N d  N d2  4ni2
N
p
 d 
2
2
n
Nd

2
N d2
 ni2
4
N d2
 ni2
4
Dispositivi a semiconduttore
12
Concentrazione portatori
n
ni
p
Dispositivi a semiconduttore
13
Dispositivi a semiconduttore
14
T
n-doping
p-doping
T alta
n=0.5Nd+ni
p=-0.5Nd+ni
p=0.5Na+ni
n=-0.5Na+ni
T
intermedia
n=Nd
p≈ni2/Nd
p=Na
n≈ni2/Na
Dispositivi a semiconduttore
15
Nd
n-doping
EF>Eg/2
intrinsic
EF≈Eg/2
p-doping
EF<Eg/2
Na
Dispositivi a semiconduttore
16
Andamento del livello di Fermi vs T al variare concentrazione droganti
Dispositivi a semiconduttore
17
Bassa temperatura: ionizzazione incompleta donori (accettori)
Un livello donore pieno contiene un solo elettrone up/down
n  NC e
n  p  N d
 Ed  Ec 
kB T 
T 0
1
N  Nd
1
B

N
(n  p)n  C (N d  n  p)e
2
N d  N d  N d0
0
d
 EF  EC 
 k T 
1
e
2
 Ed  E F 
 k T 
b
n  p  N d  N d  N d0
 Ed  E F 
 k T 
1
e b
n  p  Nd 2  E  E 
d
F
1  kb T 
1 e
2
n p0
La concentrazione di
elettroni viene
attivata con energia
pari a 1/2 energia
donore
T _ bassa
n, p  N d
n
 Ed  Ec 
2 kB T 
N c N d 
e
2
Dispositivi a semiconduttore
18
Ed  EC 1
Nd
EF  EC 
 k BT ln
2
2
2N C
Il livello di Fermi si sposta verso EC o EV a seconda del drogaggio
Dispositivi a semiconduttore
19
Doping compensation
BC
Ed
n0 doping: Nd >>Na
n=Nd-Na<n0
Ea
E F  E c  kB T ln
Nd  Na
NC
EV  E F  kB T ln
Na  Nd
NV

BV
p0 doping: Na>>Nd
p=Na-Nd<p0

Dispositivi a semiconduttore
20
Compensation
La compensazione
Dispositivi a semiconduttore
21
Applicazioni
•
Termometri a semiconduttore : R cresce al diminuire di T
•
Substrati per microelettronica: alta resistività
Dispositivi a semiconduttore
22
Si @300K
Dispositivi a semiconduttore
23
Controllo resistività con livelli profondi di impurezza
Impurezza shallow:livello vicino BC (BV)
Enhancement della conducibilità
Impurezza deep : miglioramento comportamento intrinseco
E realizzazione di substrati semi-isolanti: =107-109 cm
Ad es.: Si:Au, GaAs:Cr, InP:Fe
BC
DL
Tipica
concentrazione
residua trappole
shallow=1014/cm3
BV
Dispositivi a semiconduttore
24