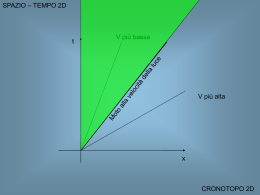
Relatività
2. La relatività ristretta
2.2 Lo spazio-tempo

Un evento nello spazio-tempo è individuato
da quattro numeri (t, x, y, z) che forniscono
l’istante t in cui il fenomeno è avvenuto e le
tre coordinate spaziali del punto in cui esso
ha avuto luogo.

Analogamente allo spazio ordinario, nello spazio-tempo esiste una
quantità, detta intervallo invariante, che dipende soltanto dai due
eventi e non dal particolare sistema di riferimento usato per descriverli.

Si chiama spazio-tempo (o spazio di Minkowski) lo spazio
quadridimensionale (t, x, y, z) nel quale l’intervallo invariante tra due
eventi è (Δσ)2 ≡ (c Δt)2 – (Δx)2 - (Δy)2 - (Δz)2
2.4 La composizione delle velocità

Un punto materiale, che ha velocità u rispetto a un sistema di
riferimento S, quando è osservato in un sistema di riferimento S’,
che si muove rispetto a S con velocità v, risulta avere velocità
u' 
uv
uv
1 2
c
u
u 'v
uv
1 2
c

Se il prodotto uv è piccolo rispetto a c2, il denominatore è
praticamente uguale a 1 e si ottiene la formula di Galileo.

Sono compatibili con il
postulato di invarianza della
velocità della luce
(esempio 2 pag. 448)
formula
inversa
2.5 L’equivalenza tra massa ed energia

La massa è una forma di energia: trasformazioni di massa in
energia e di energia in massa.

Relazione di Einstein
E = m c2

Un corpo fermo e non soggetto a forze possiede una energia di
riposo E0 per il solo fatto di avere una massa (di riposo) m0
E0 = m0 c2

Esperimenti sulle particelle elementari:
materializzazione di particelle a spese della scomparsa di energia
e, viceversa, annichilazione di due particelle con conseguente
emissione di energia
2.6 Dinamica relativistica
Energia totale
relativistica
E
m0 c 2
v
1  
c
2
  m0 c 2
la velocità della luce c risulta una velocità limite:
nessun corpo può raggiungerla né, tantomeno,
superarla (energia infinita)
Energia cinetica
relativistica
K r    1 m0c 2
Massa relativistica
è funzione della velocità
m   m0 
m0
v
1  
c
2
m0=massa di riposo (v=0)
Quantità di moto
relativistica

m0 v


p  mv 
  m0 v
2
v
1  
c