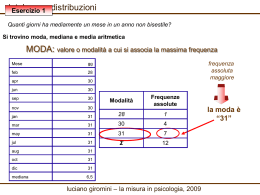
Mediana
Punto che lascia il 50 % dei casi alla sua destra
e il 50% dei casi alla sua sinistra
Esempio:
8, 9, 10, 11, 15, 6, 7
Mettere le misure in ordine crescente:
6, 7, 8, 9, 10, 11, 15
Mediana
In una distribuzione ordinata di soggetti
è il valore che taglia in due parti uguali la distribuzione
Mediana
Reparti
N. di operai
1
Poco
faticoso
2
moderat.
faticoso
3
Faticoso
4
Molto
faticoso
5
Faticoso al
massimo
TOT.
2
2
4
2
2
25
1, 1, 2, 2, 3, 3, 3, 3, 4, 4, 5, 5
50%
50%
Mediana = 3
Moda
Livello di
fatica
5
4
3
2
1
… e la moda?
F
F.C.
F.C. %
2
2
4
2
2
12
10
8
4
2
100
83
66
33
16
Moda = 3
In una distribuzione di frequenze
la moda è il valore con la frequenza semplice più alta
Media
voti
F
Fc
Fc%
30
29
28
27
26
25
24
1
3
6
4
2
2
2
20
19
16
10
6
4
2
100
95
80
50
30
20
10
Mediana = 27
… e la media?
Media
È pari alla somma di tutti i valori
della variabile cardinale per i singoli soggetti osservati
diviso per il numero totale dei casi in esame
voti
F
30
29
28
27
26
25
24
1
3
6
4
2
2
2
Media
voti
F
30
29
28
27
26
25
24
1
3
6
4
2
2
2
Media = 24 + 24 + 25 + 25 +26 + 26 + 27 +27 + 27 + 27
+ 28 + 28 + 28 + 28+ 28 + 28 + 29 + 29 + 29 + 30 /20 = 27,15
Media = (24 x 2) + (25 x 2) +(26 x 2) + (27 x 4) + (28 x6) +
(29 x3) + 30 /20 = 27,15
Scarto quadratico medio
Si usa per avere una rappresentazione
della dispersione dei dati
-3σ
- 2σ
- 1σ
+ 1σ
Media
+2
+3σ
Applicazioni dello scarto quadratico medio (σ)
Quali delle due distribuzioni
presenta una maggiore dispersione dei dati?
Distribuzione A
X = 150
σ= 10
Distribuzione B
X = 150
σ= 75
Curva normale
100% dei casi
95%
68%
-3σ
- 2σ
- 1σ
+ 1σ
Media
+ 2σ
+3σ