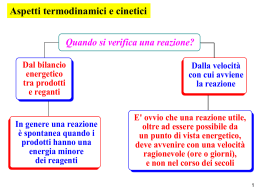
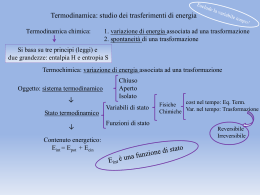
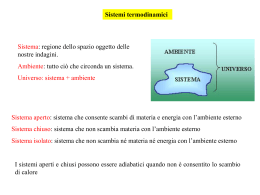
Lezione 25 –
Termochimica 1
Energia interna (E)
L'energia posseduta da un sistema viene definita Energia interna E (spesso indicata
anche come U).
L'energia interna di un sistema dipende esclusivamente dalla pressione, dalla
temperatura, dal volume e dalla composizione chimica del sistema (tipo ed
intensità delle interazioni tra particelle costituenti).
Per questo motivo l'energia interna è una funzione di stato.
Inoltre l'energia interna è una proprietà estensiva, è cioè proporzionale alla quantità
di materia presente nel sistema.
L'energia interna di un sistema chimico è uguale alla somma dell'energia cinetica e
dell'energia potenziale di tutte le molecole che formano il sistema.ed è associata ai
moti traslatori, rotazionali, vibrazionali, elettronici e nucleari delle molecole, nonché
alle interazioni interatomiche (legami intramolecolari) ed intermolecolari.
E(tot) = E(cin) + E(pot)
L’energia interna non include invece l'energia cinetica e potenziale associata al
sistema nel suo complesso, ad esempio, se il sistema è in movimento o si trova in un
campo gravitazionale o elettromagnetico.
la variazione di energia interna E che accompagna una reazione chimica risulta
uguale alla somma del calore Q e del lavoro meccanico W messi in gioco nella
reazione:
E = Q - W
Secondo la convenzione oggigiorno più comunemente impiegata, si considera positiva
l'energia termica assorbita dal sistema e negativa quella da esso perduta, e quindi
dovranno essere considerati positivi le quantità di calore somministrate al sistema
durante la reazione e viceversa negative le quantità di calore sviluppate.
Se ad esempio un sistema chimico reagisce trasformando dei reagenti in
prodotti di reazione, noi siamo in grado di misurare solo la variazione di
energia interna E che si verifica durante la reazione, espressa come differenza
tra l'energia interna dei prodotti di reazione (energia interna dello stato finale,
Ef) e l'energia interna dei reagenti (energia interna dello stato iniziale, Ei)
ΔE = Ef − Ei
Non ci è invece possibile misurare i valori assoluti di Ef ed Ei.
In un sistema isolato E = 0 e la reazione avviene per conversione interna di
una forma di energia in un'altra (cinetica in potenziale, o viceversa).
E = Q PV
Abbiamo già visto che se un sistema (chiuso) si espande a pressione
costante il lavoro meccanico di espansione può essere espresso come
prodotto della pressione gravante sul sistema per la variazione di volume
da esso subita; se V1 è il volume a reazione avvenuta, V2 il volume iniziale
e P la pressione dell'ambiente in cui avviene la reazione avremo dunque
che il lavoro compiuto dal sistema durante la reazione sarà pari a
P·(V2-V1) = P·V.
Per la convenzione sopra ricordata (positivo il lavoro sviluppato, negativo
il lavoro assorbito) si ha W = PV, da cui
E = Q - PV
Qualora la reazione avvenga senza variazione apprezzabile di volume PV = 0 e dunque
E = Q (a volume costante)
Ovvero: nelle reazioni che hanno luogo a volume costante, per esempio in un recipiente
chiuso, la variazione di energia interna è uguale al calore assorbito nel corso della reazione.
Solitamente però le reazioni vengono fatte avvenire in condizioni di pressione costante; in
questo caso la quantità di calore assorbita o ceduta dal sistema reagente nel corso della reazione
viene chiamata variazione di entalpia o, più brevemente, entalpia di reazione e indicata con il
simbolo H, avremo allora
H = Q (a pressione
costante)
Secondo la solita convenzione H si considera positivo quando la reazione avviene con
assorbimento di calore, negativo quando la reazione avviene con sviluppo di calore.
E = H - PV
Combustione del metano
CH4(g) + 2O2(g)  CO2(g) + 2H2O (g)
H(298 K) = -802 kJ
CH4(g) + 2O2(g)  CO2(g) + 2H2O (l)
H(298 K) = -890 kJ
La relazione che intercorre tra il calore di reazione a volume costante e il
calore di reazione a pressione costante:
E = H-PV
dove V = V2 – V1
Ammettendo che sia valida la legge dei gas perfetti possiamo porre :
V2 = n2·R·T / P
e
V1 = n1·R·T / P
dove n2 e n1 rappresentano il numero di molecole gassose a reazione
avvenuta e prima della reazione, da cui
V2 - V1 = (n2 - n1) · R · T / P
In definitiva
P·V = (n2 - n1) · R · T = n·R·T
dove n è la variazione del numero delle molecole gassose nel corso della
reazione.
Come esempio consideriamo la reazione :
Ni(s) + H2SO4(aq)  NiSO4 + H2(g)
H a 25 °C = -64 kJoule.
Poiché per questa reazione n = 1, il valore di E sarà dato
da E = -64 – (1 · 8,314 · 298/1000) = -66,5 kJoule.
Si indica con il nome di entalpia standard di formazione il valore che si
ottiene nel caso in cui le sostanze interessate alla reazione si trovino nel
loro stato standard e alla temperatura di 25 °C. Così, ad esempio, quando
si afferma che l'entalpia di formazione standard dell'anidride carbonica
vale –393500 Joule si intende che per la reazione :
C(s, grafite) + O2(g)  CO2(g)
a 25 °C il H è pari a -393,5 kJoule. Questo appunto perché a 25 °C e 1
atmosfera la forma stabile del carbonio è rappresentata dalla grafite,
quella dell'ossigeno e della CO2 dal gas.
legge di Hess
MgO(s) + 2HCl(aq)  MgCl2(aq) + H2O(l)
il cui H a 25 °C vale -34.900 kJoule.
La reazione può essere scissa in due reazioni parziali. In un primo tempo si può fare reagire
l'ossido di magnesio con acqua ottenendo così l'idrossido Mg(OH)2. Questo può poi essere fatto
reagire con una soluzione acquosa di acido cloridrico con formazione di cloruro di magnesio e
acqua:
MgO(s) + H2O(l)  Mg(OH)2
H = -8,800 kJ
Mg(OH)2(s) + 2HCl(aq)  MgCl2(aq) + 2H2O(l)
H = -26,100 kJ
La somma dei H delle reazioni parziali è appunto uguale a –34,900 kJoule, entalpia di
reazione della reazione complessiva.
Si voglia ad esempio conoscere il H della reazione di formazione del metano a
partire da carbonio grafitico e idrogeno a 25 °C.
C(s,grafite) + 2H2(g)  CH4(g)
Questa reazione non avviene direttamente in modo completo ed è dunque
impossibile una misura sperimentale dell'effetto termico che l'accompagna.
Sono però accessibili a una misura diretta i H delle reazioni seguenti, che
avvengono tutte con rapidità e in modo completo.
1) CH4(g) + 2 O2(g)  CO2(g) + 2 H2O(l)
H = - 890 kJ
2) C(s,grafite) + O2(g)  CO2(g)
H = - 393,5 kJ
3) 2 H2(g) + O2(g)  2 H2O(l)
H = - 571,6 kJ
Sommando le reazioni 2) e 3) e sottraendo la 1) si ricava la reazione di
formazione del metano dagli elementi. Il suo H è dunque pari a
- 75,1 kJ·mol-1.
CH4(g) + 2O2(g)

CO2(g) + 2H2O (g)
Come conseguenza immediata della legge di Hess abbiamo che il
H di una qualunque reazione è uguale alla somma
delle entalpie di formazione dei composti che si
originano nella reazione stessa meno la somma delle
entalpie di formazione delle sostanze reagenti.
Ciò perché una qualunque reazione può essere teoricamente suddivisa in
due processi parziali: uno nel corso del quale le sostanze reagenti vengono
scisse negli elementi costituenti, per il quale la variazione di entalpia è
pari all'opposto della somma delle entalpie di formazione dei reagenti, e
un secondo nel corso del quale gli elementi si ricombinano fra loro per
dare i prodotti di reazione, per il quale la variazione di entalpia è pari alla
somma delle entalpie di formazione dei prodotti.
Fe2O3(s) + 3CO(g)  2Fe(s) + 3CO2(g)
H = 2·Hf(Fe) + 3· Hf(CO2) - Hf(Fe2O3) - Hf(CO)
3x
C + O2  CO2
2x
Fe  Fe
-3 x
C + 1,5·O2  CO
-1 x 2·Fe + 1,5·O2  Fe2O3