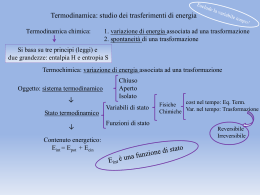
Lezione 8
Calore ed energia
Calore (Q) = forma macroscopica nella quale l'energia passa da
un sistema fisico ad un altro unicamente a causa di differenze di
temperatura. Il calore fluisce dal corpo più caldo a quello più
freddo ed essendo una forma di energia si misura in joule.
C = Capacità termica
cv = c a volume costante
Q = C·ΔT
C = m·c
T2 – T1
massa  calore specifico (c)
c può essere cp o cv
cp = c a pressione costante
Caloria
Quantità di calore necessaria ad elevare da 14,5 a 15,5 °C la
temperatura della massa di un grammo di acqua distillata a
livello del mare (pressione di 1 atm).
(piccola) caloria
Grande caloria
= cal = 4,186 J
= Cal = kcal = 4186 J
Esempio:
100 g di zuccheri, se ingeriti, forniscono ~ 400 Cal
100 g di proteine, se ingerite, forniscono ~ 400 Cal
100 g di grassi, se ingeriti, forniscono ~ 900 Cal
Nota: frigoria = caloria negativa
Sistema termodinamico
Porzione di spazio, separata dal resto dell’universo (cioè
l’ambiente esterno) mediante una superficie di controllo
(superficie reale o immaginaria, rigida o deformabile), sede di
trasformazioni interne e scambi di materia o energia con
l’ambiente esterno.
sistema aperto: sistema che può scambiare con l’ambiente
esterno sia energia (lavoro o calore) sia materia.
sistema chiuso: sistema che può scambiare con l’ambiente
esterno energia (lavoro o calore) ma non materia.
sistema (dal bordo) adiabatico: sistema chiuso che può scambiare con
l'ambiente esterno solo lavoro, ma non calore.
sistema dal bordo rigido: sistema chiuso che può scambiare con l'ambiente
esterno solo calore, ma non lavoro.
sistema isolato: sistema che non interagisce in alcun modo con
l'ambiente circostante, ovvero che non scambia massa, né
energia (lavoro o calore).
Principio 0 della termodinamica
Se un corpo A è in equilibrio termico con un corpo B, e il corpo B
è a sua volta in equilibrio termico con un altro corpo C, allora A è
in equilibrio termico con il corpo C.
Questo principio viene utilizzato per effettuare una misura della
temperatura, se viene intesa come proprietà che determina se un
corpo è in equilibrio termico con altri corpi oppure no. Due corpi in
equilibrio termico fra loro sono alla stessa temperatura.
Energia interna (U o E)
In ogni sistema è contenuta una certa quantità di energia, in varie
forme, che viene perciò definita energia interna del sistema. In un
gas questa energia è essenzialmente l'energia cinetica totale
delle molecole in movimento. Esistono due modi per modificare
l'energia interna di un corpo: fornendo calore o compiendo un
lavoro sul sistema. Sappiamo che l'energia interna del gas
dipende dalla sua temperatura, infatti maggiore è questa e più
velocemente le molecole del gas si muovono. Quando forniamo
calore ad un gas vediamo che la sua temperatura aumenta, quindi
aumenta anche la sua energia interna. Allo stesso modo se
comprimiamo il gas, facendo quindi lavoro sul sistema,
aumentiamo la sua energia interna. Da qui muove il primo
principio della termodinamica, che non è altro se non una
generalizzazione del principio di conservazione dell'energia per
cui
l'energia non si genera e non si distrugge
Principio 1 della termodinamica
Detto anche Legge di conservazione dell'energia esprime
l’assunto fondamentale della equivalenza di calore e lavoro.
Per un qualsiasi sistema
ΔE = Q – L
Q>0
L>0
Cioè, la variazione di energia interna E corrisponde alla differenza
delle quantità di calore Q e lavoro L scambiati dal sistema con
l’ambiente. L è considerato positivo quando è ceduto dal sistema
all'ambiente, Q positivo quando è ceduto dall'ambiente al sistema.
Nota1: Il primo principio implica l’impossibilità della esistenza del moto
perpetuo di prima specie.
Nota2: Per un sistema isolato l'energia è costante. L'universo è considerato
un sistema isolato.
Nota3: in alcuni testi il primo principio è scritto come ΔE = Q + L perché in quei
casi si considera per convenzione L > 0 se L entra (invece di uscire) nel
sistema.
Trasformazioni notevoli per gas
Trasformazione isoterma. In questo caso la temperatura del gas
non varia e quindi nemmeno la sua energia interna. Possiamo
quindi scrivere:
ΔE = Q – L = 0  Q = L
Tutto il lavoro che viene fornito al sistema si converte
completamente in calore e viceversa.
Trasformazione isocora. In questa trasformazione il volume
resta costante, quindi il gas non compie nessun lavoro di
espansione. Il primo principio diventa:
L = 0  ΔE = Q
Tutto il calore che viene fornito al gas va a variare la sua energia
interna e quindi la sua temperatura. Viceversa se il sistema cede
calore, la sua energia interna diminuisce e quindi il gas si
raffredda (vedi ad es. bomba calorimetrica di Mahler).
Trasformazione isobara. In questa situazione non vi è nessuna
grandezza che si conservi: infatti il sistema compie o subisce
lavoro, assorbe o cede calore e quindi la sua energia interna e la
sua temperatura variano. In questo caso è però molto semplice
calcolare il lavoro, che, come si può dimostrare, è dato dal
prodotto tra la variazione di volume e la pressione (che resta
costante):
L = p·ΔV  ΔE = Q – p·ΔV
Trasformazione reversibile. È ad esempio una trasformazione
isoterma e isobara ottenibile con variazioni infinitesimali di volume
Q = L = p·ΔV
Trasformazione adiabatica. Se il sistema è chiuso e non vi sono
scambi di calore con l'esterno, si può scrivere:
Q = 0  ΔE = -L
Nota: la resa di una macchina termica è definita come
Dove L = lavoro compiuto; Q = calore assorbito.
L

Q
Funzioni di stato
Il primo principio può essere scritto in forma differenziale:
dE = δQ – δL
Dove d indica un differenziale esatto mentre δ esprime un
differenziale non esatto. Q ed L, infatti, non sono funzioni di stato,
in quanto dipendenti dal particolare percorso compiuto nel corso
della trasformazione. Una funzione di stato (o "quantità di stato") è
una proprietà di un sistema che dipende solamente dallo stato
iniziale e finale, e non dal particolare cammino seguito per
arrivarvi. Una funzione di stato descrive perciò lo stato di equilibrio
di un sistema; per esempio, l'energia interna, l'entalpia e l'entropia
sono tutte "quantità di stato“.
Entalpia (H)
Per un sistema chiuso, è una funzione di stato definita come:
H = E + p·V
dove E è l'energia interna del sistema, p la sua pressione e V il
suo volume.
Se si deriva H e si tiene conto del 1° principio, si ottiene:
dH = dE + p·dV + V·dp

dH = δQ – δL + p·dV +
V·dp
p = costante  V·dp = 0
Se il lavoro è solo quello di espansione  δL = p·dV
Dunque, in un sistema chiuso a pressione costante e in assenza
di lavori diversi da quello di espansione (ad es. all’aria aperta):
Entalpia di reazione (ΔH o ΔHr)
Le variazioni di energia possono derivare solitamente da un
lavoro meccanico fatto o subito dal sistema o dal calore prodotto
o ceduto nel corso di una reazione chimica. Poiché le reazioni
sono solitamente studiate a pressione costanti e senza lavori
diversi da quelli di espansione, è comodo considerare i calori di
reazione a pressione costante ovvero le entalpie di reazione.
La reazione cede calore (reazione esotermica)
ΔHr = Q < 0
La reazione assorbe calore (reazione endotermica)
ΔHr = Q > 0
CO(g) + ½O2  CO2(g)
ΔH = -283 kJ (reazione esotermica)
Se viene invertita la direzione di una reazione, ΔH cambia segno:
CO2(g)  CO(g) + ½O2
ΔH = +283 kJ (reazione endotermica)
Se l’equazione viene ad esempio moltiplicata per 2, anche il ΔH
risulta moltiplicato per 2 dal momento che sono coinvolte il doppio
di moli (l’entalpia, come l’energia, è una proprietà estensiva).
2CO2(g)  2CO(g) + O2
ΔH = +566 kJ
Il fosforo rosso reagisce con bromo liquido secondo la
reazione: 2P(s) + 3Br2(l)  2PBr3(g)
ΔH = -243 kJ.
Calcolare il ΔH quando 2,63 g di fosforo reagiscono con
eccesso di bromo.
-10,31 kJ
Stati o condizioni standard
Le entalpie assolute delle sostanze, così come le energie
assolute, non possono essere misurate o calcolate. Si possono
misurare solo le variazioni.
Per far fronte a questo problema, per le sostanze chimiche, si
definiscono gli stati o condizioni standard come segue:
•Per i solidi e i liquidi è lo stato termodinamicamente stabile alla
pressione di 1 atm e ad una temperatura di riferimento.
•Per i gas è la fase gassosa con comportamento ideale alla
pressione di 1 atm e ad una temperatura di riferimento.
•Per le specie disciolte è una soluzione 1 M con comportamento
ideale all pressione di 1 atm e ad una temperatura di riferimento.
Qualsiasi temperatura può essere scelta come temperatura di
riferimento. Se non specificato diversamente essa è 298,15 K
(25°C). In questo caso si parla anche di STP o SATP.
Nota: non confondersi con la vecchia convenzione di Temperatura
e Pressione Standard (STP) per cui p = 1 atm e T = 0°C.
Entalpia (molare) standard di
formazione (ΔHf°)
di un composto ad una certa temperatura di interesse è il
cambiamento di entalpia che accompagna la formazione di 1 mole
di quella sostanza dai suoi componenti elementari, al loro stato
standard, cioè presi puri nella loro forma più stabile alla
temperatura d'interesse e alla pressione di stato-standard, che
come già detto è 1 atm (qualcuno propone 1 bar).
Si ricorda che lo stato-standard termodinamico dipende dalla
temperatura d'interesse la quale, se non espressa, si intende
298,15 K (25°C).
La entalpia di formazione di un elemento è 0 per definizione.
C(s, grafite) + O2  CO2(g)
ΔHf° di CO2 = -393,5 kJ/mol
Nota: le entalpie di formazione sono valori tabellati.
Legge di Hess
Stabilisce che in una reazione chimica il ΔH è indipendente dagli
stati intermedi attraverso i quali si evolve il sistema e dipende solo
dal suo stato iniziale e finale (infatti H è una funzione di stato).
In altre parole: il ΔH di una reazione che può essere scomposta
idealmente in più reazioni parziali è pari alla somma algebrica dei
ΔH delle singole reazioni.
C(s,gr.) + O2  CO2(g)
2CO2(g)
 2CO(g) + O2
2C(s,gr.) + O2 2CO(g)
Nota: gr. sta per grafite
ΔH1 = -393,5 kJ
ΔH2 = +566 kJ
ΔH3 = 2ΔH1 + ΔH2 = -221 kJ
Consideriamo la seguente reazione
C
+
2H2

ΔH4
CH4
Essa si può considerare come combinazione delle reazioni:
C
H2
CH4
+
+
+
O2
½O2
2O2



CO2
H2O
CO2
+
ΔH1
ΔH2
ΔH3
2H2O
Infatti moltiplicate queste per opportuni coefficienti e sommate tra
loro, ci restituiscono la reazione iniziale:
(x 1) C
(x 2) 2H2
(x -1) CO2
=
C
+
+
+
O2

O2

2H2O 
+
2H2

CO2
2H2O
CH4 +
2O2
CH4
Per la legge di Hess possiamo quindi scrivere che
ΔH4 = ΔH1 + 2ΔH2 – ΔH3
ΔH1
2ΔH2
-ΔH3
ΔH4
Date tre reazioni chimiche e il loro ΔH°
1: Fe2O3 + 3CO(g)  2Fe(s) + 3CO2(g)
ΔH1° =-26,7 kJ
2: 2C(s,gr.) + O2 2CO(g)
ΔH2° =-221,0 kJ
3: C(s,gr.) + O2 CO2(g)
ΔH3° = -393,5 kJ
calcolare il ΔH4° della seguente reazione:
4: 4Fe(s) + 3O2(g)  2Fe2O3(s)
- 1644,6 kJ
Entalpia standard di reazione (ΔHr°)
Per una certa temperatura di interesse è il cambiamento di
entalpia che accompagna la formazione dei prodotti a partire dai
reagenti presi al loro stato standard. La seguente relazione deriva
dalla legge di Hess.
H   i  H

r

f
i
i = coefficiente stechiometrico del composto i
i = prodotto  i > 0
i = reagente  i < 0
La stessa relazione può essere scritta come: (n = coefficiente
stechiometrico)
H   n prodotti  H

r

f ( prodotti)
 nreagenti  H

f ( reagentii)
Nota: Reagenti e prodotti devono essere alla stessa temperatura. Se così non
fossero bisognerebbe usare la legge di Kirchhoff.
Energia (interna molare) standard di
formazione (ΔEf°) o di reazione (ΔEr°)
Valgono le stesse considerazioni fatte per definire ΔHf° e ΔHr° in
funzione di ΔH. Poiché in genere sono tabulate le ΔHf° invece che
le ΔEf°, occorre ricordare come varia ΔE in funzione di ΔH.
Nel caso (più comune) di trasformazioni isobare (solitamente 1
atm) e in assenza di lavori diversi da quello di espansione si
ricorda che
ΔE = Q – p·ΔV & Q = ΔH 
ΔE = ΔH – p·ΔV
Se le trasformazioni includono dei gas ideali, in base alla legge
dei gas ideali (P·V = n·R·T) si ricava facilmente che
ΔE = ΔH – Δn·R·T
Sarà quindi, ad esempio: ΔEf° = ΔHf° – Δn·R·T
Calcolare l’entalpia standard di reazione e l’energia standard di reazione
dell’equilibrio di Boudouard a 25°C e 1 atm.
C + CO2  2CO
Calcolare il calore sviluppato nella combustione a 25°C e a P = 1 atm di
1dm3 di CH3OH (l) (densità = 0,8 g/cm3) con formazione di H2O liquida.
Calcolare il calore sviluppato nella combustione a 25°C e pressione
costante, di 1 m3 (misurato in condizioni normali) di una miscela gassosa
di composizione percentuale in volume:
CO = 70%; Ar = 20%; N2 = 10%
172,5 kJ; 170,0 kJ
18,16 MJ
8,84 kJ