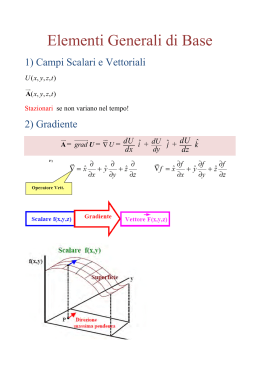
Integrali di linea,
di superficie,
di volume
5.
Integrali di linea
campo di forze
f
L  ff  r
f
B
LAVORO
f
f
f
f
f
A
f
f
B
A
f(x,y)

bb
X
LLL
Lff(f(gg((gtf(it(())))
d)ggd'(
(dgttiX())(t dt
hi )
t
))
)
g
B
aa
INTEGRALE DI LINEA di
lungo la curva
A
f(g(t1))
g
f
B
a
b
C
A
B
a
a
b
b
C
A

a b
ADDITIVITA’ :
f ( X )  dX 

a
f ( X )  dX 
 f ( X )  dX
b
B
g
A
B
g*
A

g*
f ( X )  dX  
 f ( X )  dX
g
Esercizi a pag. 428
n
R
F:
F : Rn
R
Rn
VICEVERSA :
dato
f:
n
R
n
R
esiste
n
F:R
R
tale che
F=f
F( P) : 

P
A
f ( X )  dX
P
A
F( P) : 

P
A
f ( X )  dX
P
OCCORRE CHE L’INTEGRALE
SIA INDIPENDENTE
DALLA TRAIETTORIA
A
0

g
f ( X )  dX 

a

aa
f ( X )  dX 
a
g  a
A

( X) )d X
dX
ff((XX))ddXX + f* (f X
bb

b
f ( X )  dX
B
*
b
*
b
Un’applicazione:
Campi di forze
conservativi
ed energia potenziale
LL 
BB

AA
ff((XX)) ddXX  F(
V(BA))F(
V(AB))
B
V:  F
energia potenziale
A
f
gradiente
f campo di forze conservativo
Esercizi a pag. 433
6.
Integrali di superficie
e di volume
n
X
f
x  s1 ( u, v) , y  s 2 ( u, v) z, z  s 3 ( u, v)
2
R
3
R
s
v :
v
v
S
s
D
s
u :
u
y
u
x
dS (uudu
)v (du
dv
dS
v dv
)
v
u v
v dv
dS
f
X
u
dS :
dudv
d  f  n dS  f  nf  (uuvv)dudv
FLUSSO ATTRAVERSO
INTEGRALE DI SUPERFICIE
FLUSSO TOTALE ATTRAVERSO S :


S
f  n dS
z
3
R
v
D
k
u
x
S
D
y
Integrali doppi a pag.439
v
u v
v dv
dS
X
u
( dy
dz) dx , dx  dy )
n dS  (u
du)dz
( v,dv
v
f  n dS  f1 dy  dz  f2 dz  dx  f3 dx  dy
u v
FORMA DIFFERENZIALE
BILINEARE
v dv
f
dS









xx du
du

u
u
y
du
y
u du
u
z
du
u
xx
dv
v dv
v
y
y dv
vdv
v
z
dv
v
dx  dy









u
( X ) 
 f 2
f1 

f1 ( X )dx fdx
(1X)dx
dy2 
2
x 2 
 x1
f 3 ( X ) dz
n3
f j
ff2j 
 fj f 3


dx
 j
dx
d  df
dxdx
2  dxdx3 3
 dx j

1
2
j
xx3 
xx 2
x 3


1
2
jj 
 11
3
 f j  f1  f3f j dx 3  dx1 f j


dx

dx

dx

dx

dx

j
2
j
3
j
x dx

x
 1

3
1
x 2
x 3

j  1  x1


f1
f11
f1

dx1  dx1 
dx12  dx12 
dx 3  dx1 
x1
x2
x 3
f 2
f 2
ff22

dx1  dx 2 
dx 2  dx 2 
dx23 
 dx
dx32 
dx
x1
x 2
xx33
f 3f3
f3
f 3
 dx
dx13dx
dx31 
dx 2  dx 3 
dx 3  dx 3
xx1 1
x 2
x 3
 f3 f2 
 f2 f1 
 f1 f3 




 dy  dz  
 dx  dy
 dz  dx  
 z x 
z 
 y
 x y 
 f3
f2
f1
f3
f2
f1 
rot f :  

,

,


z
z
x
x
y 
 y
ROTORE DI
f
d  rot
rotf f (ndy
dS dx , dx  dz , dz  dx )
 f3 f2 
 f2 f1 
 f1 f3 




 dy  dz  
 dx  dy
 dz  dx  
 z x 
z 
 y
 x y 
rot f  0  Jf è simmetrica
f  fIRROTAZIONALE
f
f
f
rot f :  

,

z
z
x
 y
3
2
1
3
f2
f1 
,


x
y 
  f1  fDI
ff1 
ROTORE
1

 x
  f2
Jf  
x

  f3

 x
y
 f2
y
 f3
y

z 
 f2 
z 

 f3 

z 
rot f  0  Jf è simmetrica
f  grad F  Jf  HF simmetrica
rot ( grad F )  0
Teorema
f è un gradiente  rot f  0
  f1 dy  dz  f2 dz  dx  f3 dx  dy
d  df1  dy  dz  df2  dz  dx  df3  dx  dy
f1
f2
f3
d 
dx  dy  dz 
dy  dz  dx 
dz  dx  dy
x
y
z
 f1
f 2
f 3 
d  


 dx  dy  dz
y
z 
 x
f1
f2 f3
div f :


x
y
z
DIVERGENZA DI
d  div f dxdydz
f
 g 3
g 2
g1
g 3
g 2
g1 
f  rot g :  

,

,


z
z
x
x
y 
 y
g 2 
g 3 
g1 
  g 3
  g1
  g 2
div f 




 



 
x  y
z 
y  z
x 
z  x
y 
div (rot g )  0
Teorema
f è un rotore  div f  0
dF  grad F  dX
d( f  dX )  rot f  n dS
d (g  n dS)  div g dV
rot ( grad F )  0
div (rot f )  0
Teorema
 è un differenziale  d  0
 chiusa
Teorema
g del gradiente
g
g
B

graddFF  
dXF(B )F(
 )F( A)
B
F() A
g
A
Teorema del rotore (di Stokes)
   
 rotdf n dS
S
S
S
S
S
f  dX
V
S
Vf n dS
Teorema della divergenza (di Gauss)
 
V
div f d
dV 
V

VV
Formula di Green a pag. 455
Ricerca di un potenziale
Torniamo al problema:
dato
f:
n
R
n
R
esiste
n
F:R
R
tale che
F=f
Teorema
f è un gradiente  rot f  0
Teorema delle circuitazioni
è
sufficiente
?
f è un gradiente se e solo se:

g

g
f ( X )  dX  0
Teorema
f è un gradiente  rot f  0
Teorema delle circuitazioni
è
sufficiente
?
f è un gradiente se e solo se:

g
S

0

n
dS
rot
f

n
dS
0

f (fX( X
) )dXdX 0
gg
SS
E
E
SEMPLICEMENTE
CONNESSO
Teorema
f è un gradiente  rot f  0
Esercizi a pag. 461
FINE DEL CORSO