CAP. 4 - STRUTTURA CRISTALLINA E DIFFRAZIONE
Introduzione.
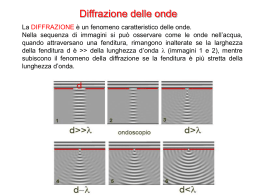
La struttura reticolare dei cristalli fu possibile iniziare ad investigarla quando
von Laue suggerì l'idea (1912) che i cristalli potessero diffrangere i raggi X.
Essendo, in un solido, le distanze interatomiche dell'ordine di 1 Å, un'onda che
possa interagire con gli atomi deve avere una lunghezza d'onda confrontabile con
tale distanza. In realtà, è possibile avere informazioni sulla struttura cristallina
studiando la figura di diffrazione prodotta oltre che da fotoni, anche da
neutroni e da elettroni. La diffrazione con raggi X richiede fotoni di energia tra
10 e 50 keV, mentre con neutroni l'energia del fascio è di circa 0.1 eV e con
elettroni di circa 100 eV (con λ≅ 1 Å ). L'interazione dell'onda con il cristallo
deve essere debole per poter penetrare un migliaio di piani reticolari e ottenere
una buona risoluzione. Quando un atomo è investito da un'onda elettromagnetica
gli elettroni dell'atomo vengono accelerati ed essi irradiano alla frequenza
dell'onda incidente (la potenza irradiata da una carica accelerata è proporzionale
al quadrato dell'accelerazione che è inversamente proporzionale alla massa, per
cui la diffrazione è dovuta agli elettroni che sono più leggeri). I raggi X
interagiscono con gli elettroni e quindi danno la distribuzione della densità
elettronica del cristallo. Se si usano elettroni, questi interagiscono con il campo
elettrico e quindi danno informazioni sulla distribuzione del potenziale. I
neutroni, invece, interagiscono essenzialmente con i nuclei perchè il potenziale
che li diffonde è diverso da zero solo sui nuclei, e quindi rivelano la distribuzione
di questi; possono interagire anche con il momento magnetico degli elettroni e
quindi possono fornire indicazioni sulla struttura di sostanze para- e
ferromagnetiche. Se si vogliono studiare gli strati superficiali gli elettroni sono
adatti perchè penetrano poco; la tecnica che si utilizza è nota come LEED, low
energy electron diffraction. Per frequenze ottiche si ha la rifrazione come
risultato, mentre per lunghezze d’onda, λ, dell'ordine della distanza interatomica
si ha la diffrazione. La relazione esistente tra lunghezza d'onda ed energia è:
per i fotoni: ε = h ν = hc/ λ ⇒ λ(Å) = 12.4/ ε (keV)
per i neutroni o elettroni: ε=p2/2M=h2/2Mλ2 ⇒
λ(Å) =0.286/
λ (Å) = 12/
ε(eV)
ε(eV)
(neutroni M=1.675 x 10-27 Kg)
(elettroni m= 9.11 x 10-31 Kg)
I raggi X sono prodotti dal bombardamento di un anodo di metallo con elettroni
veloci oppure fasci intensi sono prodotti dalla radiazione di sincrotrone. Essi
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
1
interagiscono con la materia in quanto il campo elettrico induce dei momenti di
dipolo, cioè dà luogo alla polarizzazione del cristallo. La profondità di
penetrazione dei raggi X è dell'ordine di 0.1 mm. I neutroni, invece, sono
prodotti nei reattori nucleari dall'urto di protoni con nuclei pesanti; la
profondità di penetrazione varia tra 0.1 mm nei materiali idrogenati a decine di
cm nella grafite. Il campione deve essere abbastanza sottile in modo da
diminuire la probabilità che si abbia una seconda diffusione o che, nel caso di
particelle, si abbiano due urti.
Vi sono due modi equivalenti di descrivere lo scattering di raggi X da parte di un
cristallo: quello di Bragg e quello di von Laue.
Bragg assunse il cristallo come costituito da piani atomici, speculari, paralleli e
distanti d. I fasci riflessi interferiscono in modo costruttivo dando dei picchi di
intensità della radiazione diffusa se la differenza di cammino tra i raggi riflessi
da piani adiacenti, cioè 2dsinθ, è un multiplo intero di λ:
2dsinθ = nλ (legge di Bragg)
(1)
θ
θ
θ
d
dsin θ
Assumiamo che lo scattering sia elastico in modo che la lunghezza d'onda non
vari con la riflessione. Per particolari valori di θ, i raggi riflessi da vari piani
interferiranno costruttivamente per dar luogo ad un intenso picco diffratto e ciò
è frutto della periodicità del reticolo. Ovviamente sinθ= nλ/2d≤1 ⇒ λ≤2d perciò
non si può usare luce visibile. Nella riflessione al primo ordine, di una radiazione
di lunghezza d'onda 1.54 Å da parte di un reticolo cubico di costante reticolare 4
Å si ha : θ=arcsin (λ/2d) = 11°, cioè al diminuire di λ l'incidenza diminuisce.
Questo risultato, sicuramente ben verificato sperimentalmente, si basa su una
assunzione non corretta, secondo la quale i piani si comportano come specchi, ma
se ciascun piano riflettesse perfettamente solo il primo piano vedrebbe la
radiazione e ogni lunghezza d'onda verrebbe riflessa.
Calcolo di Laue per l’ampiezza dell’onda diffusa.
Laue considera gli ioni costituenti il reticolo di Bravais come sorgenti che reirradiano la radiazione incidente, in tutte le direzioni. I picchi si osservano nelle
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
2
direzioni e per lunghezze d'onda tali che le onde scatterate interferiscano
costruttivamente. Essendo il processo base lo scattering elastico studiamo
dapprima tale processo.
La diffusione coerente dei raggi X da parte di una distribuzione di elettroni.
Vediamo innanzitutto lo scattering elastico da parte di un singolo elettrone
usando un approccio classico. E' noto dall'elettromagnetismo che un elettrone
libero investito da un campo elettrico variabile si comporta come un oscillatore;
la sua accelerazione sarà
r
e r
a=
E inc
mo
(2)
L'oscillatore irradia un campo elettromagnetico che a distanza grande rispetto
alla lunghezza d'onda e se la radiazione incidente è polarizzata, ha una intensità
media data dal vettore di Poynting:
⎛ e2 ⎞2
I =⎜
⎟ I inc sin 2 ψ
2
⎝ moc r ⎠
1
(3)
Se la radiazione incidente non è polarizzata, si deve mediare il termine
sin 2 ψ
su
r
tutte le orientazioni di E inc nel piano xy se l'onda incide lungo z (vedi figura); si
ottiene la formula di Thomson:
z
onda X incidente
Bs
E
s
r
θ
ψ
B
inc
e
ϕ
x
y
E
inc
2
r
r
r
e
e
c
c
1 E
ES × H S =
asinψ , 〈I 〉 =
〈a 2 〉sin 2 ψ =
S =
2
4 2
c r
4π c r
4π
2
⎛ e2 ⎞
c e2 e2
2
2
=
〈E inc 〉sin ψ = ⎜
⎟ I inc sin 2 ψ
2
4 2
2
4π c r m o
⎝ m oc r ⎠
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
3
dove
f 2T ( r,θ)
è
⎛ e2 ⎞2
1 + cos 2 θ
I =⎜
= I inc f 2T ( r,θ)
⎟ I inc
2
2
⎝ moc r ⎠
2
la funzione di Thomson e (1 + cos θ) / 2 è
(4)
detto fattore di
polarizzazione. Le precedenti espressioni dell'intensità media diffusa sono
espresse nel sistema di Gauss.
r
Supponiamo che una distribuzione di elettroni con densità ρ( r ) sia investita da
I inc nella direzione
r
data dal versore u o . Se l'estensione spaziale della distribuzione è piccola
un'onda non polarizzata di lunghezza d'onda λ e intensità
rispetto alla distanza in cui la radiazione diffusa viene rivelata, possiamo
assumere sferica tale onda diffusa con centro nella distribuzione. Tale onda sarà
la sovrapposizione di tutte le onde di ampiezza infinitesima prodotte dagli
elementi costituenti la distribuzione. Bisognerà tener conto dei ritardi di fase
delle onde generate da una singola onda polarizzata incidente. (vedi figura).
Fissata una origine arbitraria O, il ritardo di fase dell'onda diffusa nella
r
r
direzione u dall'elemento dV individuato dal vettore r ' , sarà dato da:
2π r r r
r ' ⋅( u − u o )
λ
(5)
dV
r'
uo
u
O
L'ampiezza del campo elettrico
cristallo sarà del tipo
r
E
dell'onda diffusa nella direzione
⎡ 2πi r r r ⎤ r 3 r
E inc C( r,θ, t ) ∫ exp ⎢
r ' ⋅( u − u o ) ⎥ρ( r ' )d r '
⎣ λ
⎦
r
u dall'intero
(6)
Integrando su tutte le possibili direzioni di polarizzazione, l'intensità diffusa
media sarà:
r
⎡ 2 πi r r r ⎤ r 3 r
r ' ⋅( u − u o ) ⎥ρ( r ' )d r '
I( u ) = I inc f 2T ( r,θ) ∫ exp ⎢
⎣ λ
⎦
2
2
la funzione di Thomson. Poniamo:
essendo f T = C
r
θ
2
1 r r
(u − u o ) = ∆k ovvero ∆k = sin
λ
λ
2
2
(7)
(8)
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
4
∆k
u
θ
2sin θ/ 2
u
La (7) può scriversi come:
dove
o
r
r 2
I (∆k ) = I inc f T2 (r ,θ ) T (∆k )
[
(9)
]
r
r
r r r
T (∆k ) = ∫ ρ (r ' ) exp 2πir '⋅∆k d 3 r '
(10)
La (10) non è altro che la trasformata di Fourier della densità elettronica
r
ρ( r )
e perciò possiamo affermare che la diffusione elastica permette di conoscere il
quadrato della trasformata di Fourier della densità elettronica.
Diffusione da parte di un singolo atomo.
Assumiamo sferica la distribuzione elettronica di un singolo atomo:
r
ρ( r ) = ρ(r )
e applichiamo l'Eq. (10) con il sistema di coordinate in figura (l'origine O coincide
con il nucleo).
q
3
d r
χ
r
O
∞
π
2π
0
0
T (∆k ) = ∫ ρ (r )r dr ∫ exp(2πi∆kr cos χ ) sin χdχ ∫ dϕ =
2
0
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
5
∞
exp(2πi∆kr cos χ )
= 2π ∫ ρ (r )r dr
2πi∆kr
0
χ =0
=
2
=
Poniamo ancora
2
ρ (r )r sin( 2π∆kr )dr
∆k ∫0
µ = 2π∆k =
4π
λ
sin
θ
(11)
per cui la (11) diventa:
2
∞
T (∆k ) = f A ( µ ) = 4π ∫ ρ (r )
0
e l'intensità diffusa
I = I inc f 2T (r, θ)f 2A (
La funzione
χ =π
∞
sin µr 2
r dr
µr
(12)
4π
θ
sin )
λ
2
(13)
f A ( µ) è detta fattore atomico di diffusione. E' evidente che il suo
calcolo richiede la conoscenza della distribuzione elettronica nell'atomo; negli
atomi leggeri essa è nota.
Vediamo ora come questi risultati si applicano al caso di un piccolo cristallo. Ogni
cella reticolare potrà essere individuata tramite le coordinate
di un suo vertice
r
ovvero tramite il vettore reticolare
r
r
r
r n = n 1 a + n 2 b + n 3 c ; il generico atomo
del cristallo sarà individuato dalla terna che individua la cella più un quarto intero
n=1, 2,.....,g che lo distingue tra i g atomi della cella; la sua posizione sarà
r
r
individuata da: r n + sν . La posizione dell'elemento di volume dV relativo
all'atomo n-esimo della cella n-esima sarà individuata da:
dove
r
sν'
r r
r r
r = r n + sν + sν'
(14)
è spiccato dal nucleo dell'atomo. Calcoliamo l'intensità diffusa dal
cristallo usando le Eq. (9) e (10). Sia
ρ ν (s' ) la distribuzione degli elettroni
nell'atomo della specie n, la distribuzione del cristallo sarà:
g
r
r
r
r
r r
r
ρ( r ) = ρ( r n + sν + s 'ν ) = ∑ ∑ ρ ν ( r − r n − sν ) =
dove
∑
( n) ν=1
g
r
∑ ∑ ρ ν ( s 'ν )
( n) ν =1
è estesa a tutte le celle del cristallo. Dobbiamo quindi calcolare
(n )
g
r
r r
r r r
r
T (∆k ) = ∫ exp(2πir ⋅ ∆k )∑ ∑ ρν (r − rn − sν )d 3 r
V
( n ) ν =1
ovvero
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
6
[
]
g
r
r r r
r
r
T (∆k ) = ∑ ∑ ∫ exp 2πi∆k ⋅ (rn + sν + sν' ) ρ ( sν' )d 3 sν'
( n ) ν =1 V
o
r
r r g
r r
r r
r
T (∆k ) = ∑ exp(2πi∆k ⋅ rn )∑ exp(2πi∆k ⋅ sν ) ∫ exp(2πi∆k ⋅ sν' )ρ ( sν' ) d 3 sν'
ν =1
(n)
V
L'integrale non è altro che il fattore atomico
f Aν (2π∆k ) relativo alla specie
atomica ν per cui la precedente può scriversi:
r
r r g
r r
T (∆k ) = ∑ exp(2πi∆k ⋅ rn )∑ exp(2πi∆k ⋅ sν ) f Aν (2π∆k )
ν =1
(n)
(15)
L'intensità diffusa sarà quindi data da:
r r
I = I inc f (r ,θ ) ∑ exp(2πi∆k ⋅ rn )
2
T
(n)
2
2
r r
∑ exp(2πi∆k ⋅ sν ) f Aν (2π∆k )
g
ν =1
(16)
La prima sommatoria è nota come fattore d'interferenza, la seconda come
fattore di struttura; entrambi dipendono da
r 2π r r
∆k =
(u − u o )
λ
cioè dalla
direzione di diffusione, fissata quella d'incidenza. Poichè la prima sommatoria
contiene moltissimi termini, al contrario della seconda, la sua dipendenza da θ è
più importante, cioè, è il fattore d'interferenza che determina le direzione lungo
cui osservare i fasci diffratti; l'altro fattore ne determina l'intensità che può a
volte annullare, anche se ammessa dal fattore d'interferenza.
r
Se il cristallo ha la forma di un parallelepipedo di spigoli
r
r
N 1 a , N 2 b , N 3 c , il
fattore d'interferenza può scriversi:
r r
∑ exp(2πi∆k ⋅ rn ) =
(n)
r r N 3 −1
r r N 2 −1
r r
∑ exp(2πin1a ⋅ ∆k ) ∑ exp(2πin 2 b ⋅ ∆k ) ∑ exp(2πin3 c ⋅ ∆k )
N1 −1
n1 = 0
n2 = 0
n3 = 0
Ciascuna somma è una serie geometrica troncata che vale:
r r
r⎞
r
i
2
N
a
π
N 1 − 1 2πin a ⋅ ∆k ⎟
1 ⋅ ∆k
∞
∞
1
e
⎠
= ∑ − ∑ =
∑ e
r r −
r r =
n1 = 0
n1 = 0 n1 = N 1 1 − e 2πia ⋅ ∆k 1 − e i 2πa ⋅ ∆k
⎛
⎜
1⎝
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
7
r r
r r
r r
i 2πN 1 a ⋅ ∆k
iπN 1 a ⋅ ∆k iπN 1 a ⋅ ∆k
1− e
1− e
⋅e
=
r r =
r r
r r =
1 − e i 2πa ⋅ ∆k
1 − eπia ⋅ ∆k ⋅ eπia ⋅ ∆k
r
r
r r
iπN 1 a ⋅ ∆k
2i sin πN 1 a ⋅ ∆k
e
r r
r r
i
π
a
⋅
∆
k
2
i
sin
π
a
⋅ ∆k
e
Moltiplicando per la complessa coniugata si ha che:
2
∑
(n)
r r
r r
r r
sin 2 N 1πa ⋅ ∆k sin 2 N 2πb ⋅ ∆k sin 2 N 3πc ⋅ ∆k
r r ×
=
r r ×
r r
sin 2 πa ⋅ ∆k
sin 2 πb ⋅ ∆k
sin 2 πc ⋅ ∆k
(17)
Le tre frazioni sono note come funzioni di Laue. Esse sono del tipo:
sin 2 Nπx
y(x) =
sin 2 πx
(18)
Tale funzione è periodica di periodo 1 e quindi basta studiarla nell'intervallo [0,
1]. N è almeno dell'ordine del migliaio per cui la funzione risulta
significativamente diversa da zero solo agli estremi dell'intervallo, cioè per x
2
intero (0 oppure 1). Per x=0, si ha un massimo che vale N ; si hanno massimi ogni
volta che Nx=(m+1/2), m=0, 1, 2,........ che per πx<<1 valgono
y= N / π
2
2
[ m ± (1 / 2 ) ]2
(19)
questi massimi o sono molto più piccoli di quello principale o gli sono molto vicini
che si confondono con esso. Possiamo quindi dire che il fattore d'interferenza ha
2 2
2
un valore molto grande N 1 N 2 N 3 solo quando i denominatori delle funzioni di
Laue si annullano, cioè quando si verificano le condizioni di Laue-Bragg:
r r
r r
r r
a ⋅ ∆k = u , b ⋅ ∆k = v , c ⋅ ∆k = w
(20)
con u, v, w interi. Le (20) determinano le direzioni lungo cui si possono osservare
i fasci diffratti, fattore di struttura permettendo. Il primo zero del
r r
r r
sin N 1πa ⋅ ∆k si ha quando a ⋅ ∆k = u + ε essendo ε il più piccolo numero
diverso da zero per cui sin N 1πε =0; si ottiene ε=1/N1.
La larghezza del massimo risulta essere pertanto proporzionale a 1/N1N2N3 e
l'area racchiusa dal massimo centrale, essendo larghezza per altezza
2 2
2
(proporzionale ad N 1 N 2 N 3 ), sarà proporzionale ad N1N2N3.
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
8
2
sin 20x
2
sin x
100
10
1
0.1
0.3
0.5
x
Considerando le equazioni (20), se gli assi sono perpendicolari tra loro, una
soluzione è data da:
r u
v
w
∆k = aˆ + bˆ + cˆ
a
b
c
Se gli assi non sono paralleli è conveniente introdurre il concetto di reticolo
reciproco.
r
r r
r
r
r
∆k = qA + rB + sC , con q, r, s, interi e determiniamo i vettori A , B ,
r
r
C in modo che ∆k soddisfi le equazioni di Laue. Si devono verificare le seguenti
Poniamo
condizioni:
r r
A ⋅ ar = 1 ;
r
Ar ⋅ b = 0 ;
r
A⋅c = 0;
r r
r r
B ⋅ ar = 0 ; C ⋅ ar = 0 ;
r
r
Br ⋅ b = 1 , Cr⋅ b = 0 ;
r
r
B ⋅c = 0; C ⋅c = 1
Si trova facilmente che tali condizioni sono soddisfatte da:
r r
r r
r r
r
r
r
b ×c
c×a
a×b
A= r r r; B= r r r; C = r r r
a ⋅b ×c
a ⋅b ×c
a ⋅b ×c
2
Mentre il reticolo diretto appartiene allo spazio reale, quello reciproco, i cui punti
reticolari sono sono individuati dai vettori
r
r
r
r
∆k = qA + rB + sC , appartiene allo
Altri autori definiscono i vettori del reticolo reciproco moltiplicando per 2π le espressioni
sopra riportate.
2
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
9
spazio di Fourier. Se moltiplichiamo scalarmente un vettore del reticolo diretto,
, con uno del reticolo reciproco,
e
r
G,
r
ρ
otteniamo un numero intero e quindi
r r
= 1, pertanto se ∆k = G , le equazioni di Laue sono soddisfatte.
r r
2πiρ ⋅G
Alcune proprietà del reticolo reciproco.
I proprietà. Ogni vettore del reticolo reciproco è perpendicolare ad un insieme
di pianir reticolari
r del rreticolordiretto.
Sia K = k 1b1 + k 2 b2 + k 3 b3
un vettore del reticolo reciproco e
r
r
r
r
R = n1a1 + n2 a2 + n3 a3 un vettore del reticolo diretto. Abbiamo visto che
r r
K ⋅ R = intero.
Consideriamo un piano cristallografico di indici di Miller (hkl)
r
r
intersecante gli assi cristallografici nei punti individuati dai vettori n1a1, n 2 a 2 ,
r
r
n a . Il vettore K sarà perpendicolare a tale piano se il prodotto scalare tra
3 3
r
K
ed un qualunque vettore reticolare appartenente al piano è zero. In
particolare,
in figura, deve aversi:
r
r
r considerando i vettori
r
r
r
r
r
r
K ⋅ (n 1 a 1 − n 2 a 2 ) = K ⋅ (n 1 a 1 − n 3 a 3 ) = K ⋅ (n 2 a 2 − n 3 a 3 ) = 0
ovvero:
k1n 1 − k 2 n 2 = k1 n1 − k 3n 3 = k 2 n 2 − k 3 n3 = 0
da cui: k 1 n 1 = k 2 n 2 = k 3 n 3 . Una soluzione, a meno di un fattore intero, è:
k1 = 1 / n 1 , k 2 = 1 / n 2 , k 3 = 1 / n 3 .
n2 a 2 - n a
3
3
n a
3
3
n a - n a
1 1
3 3
n a
1
1
n2 a 2
n a - n2 a
1 1
2
Ma
1 / n 1 ,r1 / n 2 , 1 / n 3 non sono altro che gli indici di Miller del piano (hkl) e
pertanto K è perpendicolare al piano e a tutti quelli ad esso paralleli.
II proprietà. La separazione
k, l vale
d (hkl )
dei piani cristallini individuati dagli indici h,
r
d (hkl ) = 1 / K1 ( hkl )
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
10
r
essendo K 1 il vettore più corto in quella direzione.
Infatti sia r un vettore del
r reticolo diretto che va dall'origine (arbitraria) O al
r
piano cristallino (hkl) e K = uK un vettore del reticolo reciproco che, per il
teorema precedente, è normale al piano. La proiezione di r nella direzione u sarà:
r
r r K r
u ⋅ r = ⋅ r = d.
K
Inoltre,
r r
K ⋅r = N
con N intero, per cui
N
d= r
K (hkl )
è la
distanza dall'origine del piano considerato.
O
u .r =d
ud
r
P
Possiamo trovare un vettore r'' tale che
r r
r ' '⋅K = ( N + 1)
La distanza tra due piani consecutivi sarà pertanto
.
.
.
.
.
.
.
.
.
d''
.
.
.
.
.
.
d.
.
.
.
.
.
.
.
.
.
.
.
.
r
.
.
. . .
. . .
. . .
. . .
. . r''.
. r' . .
per cui
1
d= r
K (hkl )
N +1
d''= r
K (hkl )
.
.
.
.
.
.
.
.
Il volume di una cella unitaria del reticolo reciproco è inversamente
proporzionale al volume di una cella unitaria del reticolo diretto.
r r r (ar × ar ) ⋅ [(ar × ar ) × (ar × ar )]
Infatti:
Vr .r . = b1 ⋅ b2 × b3 = 2 3 r 3r 1r 3 1 2
[a1 ⋅ a2 × a3 ]
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
11
r r
r r r r
r r r r
r r
r
(
a2 × a3 ) ⋅ {[a3 ⋅ (a1 × a2 )]a1 − [a1 ⋅ (a1 × a2 )]a3 } (a2 × a3 ) ⋅ Vr .d .a1 =
=
=
Vr3.d .
2
= Vr .d . = 1
Vr3.d . Vr .d .
Vr3.d .
3
Si può provare che il reciproco del reticolo reciproco è il reticolo diretto,
cioè, definiti i vettori ci come
r r
b ×b
j k
r
c = r r r
i
b ⋅⎜⎛ b ×b ⎞⎟
i ⎝ j k⎠
si ha ci=ai.
Calcoliamo, come esempio, il reticolo
reciproco
r
r di un reticolo
r cubico semplice i cui
r
r
r
a 3 = ak ; per definizione:
a 1 = ai , a2 = aj ,
r r
r
a 2 × a3
a2 r 1 r
b1 = r r r = 3 i = i
a1 ⋅ a 2 × a 3 a
a
r 1r
r
1r
j e b3 = k ; quindi il reticolo reciproco é ancora
e analogamente b2 =
a
a
vettori
base
sono
cubico semplice. Se il reticolo diretto è fcc, i vettori primitivi sono:
a r r r
a r r r
a r r
r
a1 = ( j + k ) , a2 = ( k + i ) , a3 = ( i + j ) .
2
2
2
k
a1
a2
i
a3
j
reticolo cubico fcc
I vettori del reticolo reciproco saranno:
r r
r
a 2 × a3
1 r r r
b1 = r r r = ( j − i + k ) ,
a1 ⋅ a 2 × a 3 a
3
r r r
r r r r r r
(a × b ) × c = (a ⋅ c )b − ( b ⋅ c )a .
Se la definizione dei vettori del reticolo reciproco è quella riportata nella nota 2, la relazione
sarà:
Vr.r. = 8π 3 /Vr.d.
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
12
r
2π r r r
b2 =
( i + k − j ),
a
r
2π r r r
b3 =
( i + j − k) .
a
che sono i vettori primitivi di un reticolo bcc di lato
2 /a. 4
reticolo cubico a corpo centrato
z
k
b
3
b1
b
i
2
j
y
x
•
La cella unitaria del reticolo reciproco è la zona di Brillouin che si ottiene
costruendo la cella di Wigner e Seitz per il reticolo reciproco.
Calcolo del fattore di struttura.
g
Dalla (16) il fattore di struttura è dato da:
∑e
rr
2πi∆k ⋅ sν
ν =1
f Aν .
Calcoliamo tale
fattore nel caso di un reticolo bcc (Na metallico). Supponiamo che la base sia
costituita da ratomi identici situati in (0,0,0) e (1/2,1/2,1/2); i vettori
r
r
r
sν = u ν a + v ν b + w ν c hanno pertanto le terne u 1 = v 1 = w1 = 0
u 2 = v 2 = w 2 = 1 / 2 . Il fattore di struttura FS varrà pertanto:
2
2
r r
FS= ∑ fν exp(2πi∆K ⋅ sν ) = ∑ fν exp[2πi (uν h + vν k + wν l )]
ν =1
e
ν =1
= f {1 + exp[iπ( h + k + l )]}
essendo f il fattore di scattering atomico. FS è zero ogni volta che exp=-1, cioè
ogni volta che h+k+l è un intero dispari, mentre FS=2f quando h+k+l è un intero
pari. Nel caso del Na metallico, lo spettro di diffrazione non contiene le righe
del tipo (100), (300), (111), (221), mentre sono presenti righe del tipo (200),
(110), (222).
4
r
b1 = 3 / a = d / 2 = 3l / 2 ⇒ l = 2 / a
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
13
Consideriamo un reticolo fcc avente la base costituita da atomi identici in
(0,0,0), (0,1/2,1/2), (1/2,0,1/2), (1/2,1/2,0). Il fattore di struttura è:
FS = f {1 + exp[iπ(k + l ) ] + exp[iπ( h + l) ] + exp[iπ(h + k )]}
Se gli indici sono tutti pari o tutti dispari, FS=4f. Se, invece, uno solo degli interi
è pari o dispari FS sarà zero. Perciò nel reticolo fcc non vi potranno essere
riflessioni per le quali gli indici sono in parte dispari e in parte pari.
(200)
KCl
(220)
(222)
(420)
(400)
80°
20 °
50°
Dipendenza dalla temperatura dell’intensità delle righe del fascio diffratto.
r
r r
Sia ρ (t ) = ρ o + u (t ) il vettore che individua la posizione di un atomo, somma di un
r
vettore ρ o che individua la posizione dell’atomo in assenza di vibrazioni e un
r
vettore u(t ) che individua lo spostamento istantaneo a causa delle vibrazioni
termiche. L’ampiezza dell’onda diffratta si può scrivere come:
r
r
A = Ao e iu ⋅∆k
Sviluppando in serie l’esponenziale si ha:
r r
r r 1 r r2
e iu ⋅∆k = 1+ i u ⋅ ∆k +
u ⋅ ∆k + ......
2
r
Essendo il moto dell’atomo casuale e scorrelato da ∆k , il secondo termine è nullo
1 2
r r2
e il terzo può scriversi come: u ⋅ ∆k =
u ∆k 2 , 1/3 deriva dalla media
3
geometrica in tre dimensioni. Per una qualunque fluttuazione gaussiana avente
(
(
ϕ = 0 , si trova
e
iϕ
=e
− ϕ2 /2
)
)
per cui
e
r r
iu ⋅∆k
≈e
−
1 2
u ∆k 2
6
. Se indichiamo
con Io l’intensità diffratta in assenza di vibrazioni, l’intensità sarà data da:
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
14
I diff = I oe
− ∆k 2 u 2 / 3
il fattore esponenziale è noto come fattore di Debye-Waller.
1
3
mω 2 u 2 = kT ,
2
2
Hz, la frequenza delle vibrazioni reticolari. L’intensità vale
Possiamo prendere come energia media dell’atomo
essendo ω= 1013 – 1014
quindi:
E =
I diff = I o exp( − kT∆k 2 / mω 2 ) , cioè diminuisce all’aumentare di T.
Quantisticamente a T=0, E =
1
3
mω 2 u 2 = hω e quindi
2
4
I diff = I o exp( −h∆k 2 / 2mω ) .
Posto ∆k =109 cm-1, ω= 1014 Hz, m=10-22 g, l’esponenziale vale circa 0.997 e quindi
I diff ≈ I o .
Metodi sperimentali per la diffrazione.
Metodo di Laue. Un fascio di lunghezza d'onda variabile con continuità tra lo e l1
investe un cristallo fermo. E' un metodo opportuno per la determinazione
dell'orientazione del cristallo. Il fascio diffratto può essere osservato o in
trasmissione o in riflessione. Il metodo di Laue non è usato per determinare la
struttura perchè su una stessa macchia possono confluire riflessioni da uno
stesso piano di ordini diversi.
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
15
Metodo del cristallo rotante. Il fascio X è monocromatico e il campione può
ruotare intorno ad un asse fisso. La pellicola è su un cilindro rotante concentrico
all'asse. Ogni volta che si verifica la condizione di Bragg il fascio è diffratto.
Metodo delle polveri o di Debye-Scherrer. Il fascio monocromatico colpisce un
campione polverizzato o policristallino. Si ha la diffrazione da tutte le possibili
orientazioni. L'intensità diffratta è proporzionale al fattore di struttura:
2
f .
Si utilizzano rivelatori di piccola accettanza angolare al posto della pellicola
fotografica usato nel metodo di Laue.
V.AUGELLI, Fisica degli Stati Condensati, Cap.4 – Struttura cristallina e diffrazione.
16