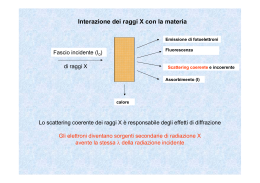
DIFFRAZIONE DA RAGGI X NEI
CRISTALLI
DIFFRAZIONE
DI RAGGI X
Ulderico Wanderlingh
9 gennaio
2006
Ulderico
Wanderlingh
1 dicembre 2005
Dipartimento di Fisica, Università di Messina – [email protected]
IndiceIndice
0.1
0.2
0.3
0.4
0.5
0.1 Reticolo Cristallino . . . . . . . . . . . . . . . . . . .
0.2 Produzione
e rilevazione
Reticolo
Cristallino
. . . .dei. Raggi
. . . X. . .. .. . .. .. . . . ..
0.3 Diffrazione di raggi X da strutture cristalline . . . .
Diffrazione
di raggi X da strutture cristalline
0.4 Intensità della diffusione . . . . . . . . . . . . . . . .
Intensità0.4.1
dellaFattori
diffusione
geometrici . . .. .. . .. .. . . . .. .. . .. .. . . . ..
0.4.2 Fattori di forma
. . . . . . . . . . .. .. . .. .. . . . ..
Analisi quantitativa
e qualitativa
0.5 Analisi quantitativa e qualitativa . . . . . . . . . . .
. . .
.. . ..
. . .
. .
. . .
.. . ..
.. . ..
. . .
.
..
.
.
.
..
..
.
. .
. ..
. .
.
. .
. ..
. ..
. .
2
. 9.
14
. 23
.
. 23.
. 24.
30
.
.
.
.
Produzione e rilevazione dei Raggi X . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
. 1
. 6
. 10
. 12
. 14
1 Reticolo Cristallino
– Preparato il 27 Aprile 2002, ultima modifica 9 gennaio 2006–
Uno dei modi
di aggregazione della materia condensata è lo stato cristallino, più del 90% dei solidi si presentano
in questa forma. Un cristallo è
1
formato macroscopicamente da un poliedro regolare la cui struttura interna
è costituita dal ripetersi periodico di una struttura elementare, detta base o
motivo, sui nodi di un reticolo tridimensionale. L’ordine interno si estende
nel caso ideale su distanze infinite, nei casi reali tale ordinamento è invece
limitato dai vari tipi di difetti reticolari.
0.1. Reticolo Cristallino
2
0.1 Reticolo Cristallino
Uno dei modi di aggregazione della materia condensata è lo stato cristallino,
più del 90% dei solidi si presentano infatti sotto questa forma. Un cristallo
è formato macroscopicamente da un poliedro regolare la cui struttura interna è costituita dal ripetersi periodico di una unità elementare, detta base o
motivo, sui nodi di un reticolo tridimensionale. L’ordine interno si estende
nel caso ideale su distanze infinite, nei casi reali tale ordinamento è invece
limitato dai vari tipi di difetti reticolari.
Lo strumento principale per lo studio dei reticoli cristallini è la diffrazione
di raggi X. Storicamente i primi studi di questo genere sono dovuti a Laue,
che con i suoi esperimenti nel 1912 dimostrò simultaneamente la natura
ondulatoria dei raggi X e la regolarità della struttura interna dei cristalli.
Prima ancora della utilizzazione dei raggi X nello studio dei solidi cristallini sono stati definiti sei sistemi fondamentali di simmetria delle strutture cristalline, un elenco è dato in tabella 1 .
Sistema
Triclininico
(1)
Monoclininico
(2)
Ortorombico
(4)
Tetragonale
(2)
Esagonale
(1)
Romboedrico o Trigonale
Cubico
(1)
(3)
Assi e angoli
a != b != c
α != β != γ != 90◦
a != b != c
α = γ = 90◦ != β
a != b != c
α = β = γ = 90◦
a = b != c
α = β = γ = 90◦
a = b != c
α = β = 90◦ γ = 120◦
a=b=c
α = β = γ != 90◦
a=b=c
α = β = γ = 90◦
Tabella 1: I 14 reticoli di Bravais
Questo è stato reso possibile da considerazioni sulla struttura macroscopica esterna dei cristalli, considerazioni riguardanti la simmetrie, gli angoli
tra le facce e i rapporti tra le dimensioni dei lati, che sono ovviamente legati
alla forma della cella elementare.
Di seguito sono sintetizzate alcune definizioni utili nella descrizione dei
cristalli:
0.1. Reticolo Cristallino
Figura 1: I 14 reticoli di Bravais
3
0.1. Reticolo Cristallino
4
– Reticolo spaziale diretto, o di Bravais. Questo è l’insieme dei punti nello spazio reale che individuano le posizioni della base. Se consideriamo
un qualunque punto del reticolo come origine, tutti gli altri punti risultano
raggiungibili con il vettore $l definito da
$l = l1$a + l2$b + l3$c
dove l1 , l2 , l3 sono numeri interi e $a, $b, $c sono i vettori fondamentali che definiscono le distanze e gli angoli tra il punto origine ed i suoi vicini. Il reticolo
diretto è dunque l’insieme dei vettori $l. L’osservazione di un reticolo risulta
uguale a se stessa quando è vista da punti che differicono per un vettore di
reticolo $l. Si possono realizzare quattordici tipi diversi di struttrure reticolari tridimensionali che se impacchettate riempiono lo spazio (Bravais), figura
1.
– Cella unitaria. Unendo tra loro i punti di un reticolo spaziale si ottengono dei parallelepipedi detti celle unitarie. La struttura cristallina è ottenuta
dall’impacchettamento di tali celle unitarie. La scelta della cella unitaria
non è unica, come si può vedere dalla figura 2, la scelta è fatta in base a considerazioni di simmetria e di semplicità matematica.
Figura 2: Un reticolo spaziale con diverse celle unitarie alternative
evidenziate.
La cella unitaria definita dai vettori fondamentali di traslazione a, b, c è la
cella primitiva, figura 3. Una cella primitiva ha volume minimo e contiene
un solo punto di reticolo. Il suo volume è dato da V = |a ∧ b · c|
– Cella di Wigner-Seitz. E’ così detto lo spazio intorno ad un punto del reticolo delimitato dai piani bisettori perpedicolari ai segmenti congiungenti
quel punto con punti reticolare vicini. Il suo volume è uguale a quello della
cella primitiva.
0.1. Reticolo Cristallino
Figura 3: Reticolo cubico a corpo centrato: a) Cella unitaria, cubo con due
punti per cella, b) Cella primitiva, romboedro con un punto per cella e
volume la metà.
– Gruppi puntuali. Oltre alla simmetrie traslazionali i reticoli posseggono
anche simmetrie puntuali, ovvero relative all’intorno di un punto.
Un gruppo puntuale è un insieme di operazioni di simmetria che lasciano invariato il sistema. Le principali operazioni di simmetria illustrate in
fig.4 sono le seguenti:
Figura 4: Principali operazioni di simmetria
1. Inversione: se esiste un punto (centro di inversione) per cui la sostituzione di $r (distanza dal punto) in −$r lascia invariato il reticolo
2. Riflessione: se esiste un piano per cui la sostituzione di d$ (distanza dal
piano) in −d$ lascia invariato il reticolo
3. Rotazione: se esiste un asse per il quale una rotazione di 2π/n lascia
invariato il reticolo, n è un intero che definisce il tipo di simmetria
(unaria, binaria terneria ....)
5
0.1. Reticolo Cristallino
6
4. Roto-inversione: una combinazione di 1 e 3.
— Base e Struttura Cristallina. Ad ogni punto del reticolo si associano, come
detto, uno o un gruppo di atomi che costituiscono la base, fig:5. Questa si
ripete in ogni punto del reticolo con la stessa disposizione ed orientazione.
La struttura cristallina risulta dall’aggiunta di una base su di un reticolo
spaziale astratto. La posizione degli i-esimo atomo della base nella cella
unitaria è definita dal vettore delle coordinate atomiche $ui$vi w
$ i ; ciascuna di
queste è un vettore le cui componenti sono una frazione della lunghezza dei
vettori fondamentali e la cui direzione coincide con quella di questi.
Figura 5: Struttura cristallina come risultato dell’aggiunta di una base ai
punti del reticolo cristallino
— Posizione di un piano in un cristallo, indici di Miller. Sui punti del reticolo spaziale si possono fare passare famiglie di piani paralleli detti piani
reticolari. Ogni famiglia di piani è individuata da tre numeri interi, gli indici
di Miller, ciascuno dei quali indica in quante parti è sezionato il corrispondente spigolo della cella elementare. Per stabilire gli indici di Miller, che
permettono di individuare l’orientazione di un piano cristallino, si considerano le intercette pa, qb, rc del piano con i tre assi principali, individuati dai
vettori (abc), come illustrato in figura 6.
Si definiscono quindi gli indici di Miller per quel piano la terna formata
dai più piccoli numeri interi (hkl) che soddisfa alla seguente relazione:
h : k : l = 1/p : 1/q : 1/r
che viene indicata con (hkl). L’insieme dei piani equivalenti dal punto di
vista della simmetria viene indicato con {hkl}. Un evetuale segno negativo
viene collocato sopra l’indice stesso. Gli indici di Miller sono legati ai coseni
direttori della normale n al piano che rappresentano, tramite la relazione:
cos α : cos β : cos γ = 1/pa : 1/qb : 1/rc = h/a : k/b : l/c
In figura 7 sono indicati alcuni piani del reticolo cubico.
Come si può notare le diverse famiglie di piani sono spaziate in maniera
diversa, le formule per fornire la spaziatura d in funzione degli indici di
Miller nei sei sistemi di struttura cristallina sono illustrate in tabella 2.
0.1. Reticolo Cristallino
Figura 6: Procedura per determinare gli indici di Miller.
Figura 7: Denominazione di alcuni piani di un reticolo cubico con gli indici
di Miller.
7
0.1. Reticolo Cristallino
8
Tabella 2: Formule per il calcolo della spaziatura interplanare, dhkl .
— Reticolo Reciproco. Il reticolo reciproco è un modo diverso di guardare
al reticolo nello spazio reale, considerandolo in termini di periodicità piuttosto ($k) che di posizione ($x). Il reticolo reciproco puo ottenersi dal reticolo
diretto sia tramite l’operazione della Trasformata di Fourier che tramite una
costruzione geometrica.
I punti che formano il reticolo reciproco risultano legati ai piani{hkl} del
reticolo diretto. I due reticoli condividono un origine comune O, e ad una
famiglia di piani nel reticolo diretto corrisponde un vettore nel reticolo reciproco, con la direzione della normale ai piani, passante per O e modulo
inversamente proporzionale alla spaziatura tra la famiglia di piani {hkl},
vedi figura 8
Matematicamente questo corrisponde a definire la terna fondamentale A, B, C
dei vettori del reticolo reciproco quella legata alla corrispondete terna nel
reticolo diretto a, b, c dalle relazioni:
A = 2π
b∧c
a · b ∧ c.
B = 2π
c∧a
a · b ∧ c.
C = 2π
a∧b
a · b ∧ c.
Il reticolo reciproco è costruito dai punti la cui posizione è individuata dai
vettori G = g1 A + g2 B + g3 C , con g1 , g2 , g3 interi.
Se consideriamo li un vettore nello spazio spazio diretto e Gk uno nello
spazio reciproco sussiste la relazione
li · Gk = 2πδik
0.2. Produzione e rilevazione dei Raggi X
Figura 8: Costruzione di un reticolo reciproco planare, e illustrazione di
reticolo reciproco cubico.
Si verifica inoltre che:
• Il reticolo reciproco è dello stesso tipo di quello diretto, e l’applicazione della suddetta trasformazione al reticolo reciproco ricostruisce
il reticolo diretto.
• Il vettore di reticolo reciproco: G(g1 , g2 , g3 ) = g1 A+g2 B+g3 C è normale
al piano individuato nel reticolo diretto dagli indici (g1 , g2 , g3 )
• Il modulo del vettore di reticolo reciproco G(g1 , g2 , g3 ) è legato all’inverso della spaziatura tra due successivi piani reticolari che individua
nello spazio diretto:
G(g1 , g2 , g3 ) =
2π
d(g1 , g2 , g3 )
• Il volume della cella primitiva nel reticolo reciproco, Vr è legato al corripondente volume nella cella primitiva, Vd , del reticolo diretto dalla
relazione:
8π 3
Vr =
Vd
0.2 Produzione e rilevazione dei Raggi X
— Origine dei raggi X. Il principale processo di produzione di raggi X è la
collisione tra elettroni veloci e la materia (bersaglio). Questo da luogo a
9
0.2. Produzione e rilevazione dei Raggi X
due fenomeni di irradiazione: la radiazione da frenamento e la radiazione
caratteristica.
La radiazione da frenamento è prodotta dal rallentamento delgli elettroni incidenti nell’attraversare il campo elettrico repulsivo degli atomi del bersaglio. Questo è un processo quantistico e la variazione di energia degli elettroni ∆E appare in forma di quanti di radiazione di frequenza ν = ∆E/h.
La radiazione emessa è indipendente dal tipo di bersaglio ed appare come
una banda continua di lunghezze d’onda la cui intensità ed il cui limite inferiore sono legati alla massima energia degli elettroni incidenti. Ne caso
di un elettrone accelerato da un potenziale V si ha un perdita massima di
energia: ∆E = V e da cui una radiazione di frequenza massima ν = V e/h e
di lunghezza d’onda minima λmin = hc/V e ovvero λmin = 12.400/V con V
in volt e λ in Å.
La radiazione caratteristica è invece presente quando l’energia degli elettroni incidenti è sufficiente ad ionizzare l’atomo rimuovendo un elettrone
dai livelli più interni. In questo caso un elettrone dai livelli più esterni và
ad occupare l’orbita lasciata libera emettendo un quanto di radiazione di
frequenza proporzionale al salto in energia tra i due livelli. Questa emis-
Figura 9: Distribuzione della radiazione vs. λ per un bersaglio di Mobildeno
ed uno di Cu con differenti tensioni acceleratrici.
sione si presenta come un intenso spettro a righe, sovrapposto alla banda
continua della radiazione di frenamento (vedi fig. 9). La frequenza delle
righe nella radiazione caratteristica è proporzionale al numero atomico del
10
0.2. Produzione e rilevazione dei Raggi X
bersaglio e le righe sono identificate dal nome del livello da cui avviene la
transizione elettronica, in analogia con il caso ottico (vedi fig. 10).
Figura 10: Diagramma schematico delle transizioni delle shell più interne.
— Generatori di raggi X. I più semplici generatori di raggi X sono formati
da un tubo in vetro fornito di due elettrodi (Anodo e Catodo) riempiti di
un gas alla pressione di qualche frazione di mm di mercurio. Quando una
sufficientemente elevata tensione è applicata agli elettrodi gli elettroni e gli
ioni, normalmente presenti in piccole quantità nel gas, si muovono verso
i rispettivi elettrodi. Gli ioni positivi collidendo con il catodo e con le alre
molecole del gas producono altri elettroni che vengono proiettati verso l’anodo o target. Nella collisione di quest’ultimi con l’anodo o le pareti stesse
del vetro si ha la produzione di radiazione X. Il principale svantaggio di tali
generatori sono l’interdipendenza della corrente dalla tensione, ed il fatto
che la pressione del gas varia leggermente durante il funzionamento, alterando le caratteristiche del tubo. I vantaggi sono ll basso costo e l’economia
di installazione e di manutenzione.
Un notevole miglioramento di questi generatori è ottenuto con i tubi a catodo caldo. In questo caso il catodo e costituito da un filamento metallico
portato ad incandescenza, e la produzione di elettroni avviene per effetto
termoionico, come illustrato in fig. 11 . La corrente viene così variata agendo sulla temperatura del filamento e risulta indipendente dalla tensione.
Inoltre la pressione può essere ridotta al minimo possibile non essendo necessario del gas residuo per avviare la produzione di elettroni. Questi tubi
risolvono i problemi del caso precedente ma sono più costosi e meno robusti. Soffrono inoltre per l’inquinamento della superficie del bersaglio da
parte dei vapori metallici prodotti dal filamento (generalmente Tungsteno).
Nei moderni generatori di raggi X l’efficienza globale è migliorata utilizzando diversi accorgimenti quali: finestre di Berillio per la fuoriuscita della
11
0.2. Produzione e rilevazione dei Raggi X
Figura 11: Schema di un moderno generatore di raggi X.
radiazione con il minimo assorbimento; raffreddamento ad acqua del bersaglio o l’utilizzo di un bersaglio rotante per minimizzare gli effetti del eccessivo riscaldamento; una particolare forma per il catodo e per il bersaglio
per focalizzare al meglio il fascio di radiazione prodotta ed infine la possibilità di disporre di più di un bersaglio per estendere il range di luinghezze
d’onda disponibili.
— Assorbimento dei raggi X. Nonostante i raggi X attraversino facilmente
la maggior parte dei materiali essi sono anche in piccola percentuale assorbiti da questi. L’andamento dell’intensità trasmessa I rispetto a quella incidente I0 , è fornita dalla legge di Lambert-Beer: I = I0 exp (−µ(λ)/x) dove
x è lo spessore attraversato e µ il coefficiente di assorbimento lineare. Una
forma più conveniente per questa espressione è in termini del coefficiente
di assorbimento di massa µm = µ/ρ:
I = I0 exp (−µm (λ)ρ/x)
Il coefficiente µm non dipende infatti dallo stato fisico chimico del materiale
a differenza di µ. E’ questa una notevole proprietà che differenzia i raggi X
dalla radiazione visibile. Ad esempio mentre il Carbonio nella forma di diamante e di grafite ha un comportamento totalmente opposto nei confronti
della trasparenza alla luce visibile, per la radiazione X mostra invece lo stesso coefficiente di assorbimento di massa.
Il coefficiente di assorbimento dipende dalla lunghezza d’onda e diminuisce con questa, a parte alcune discontinuità in corrispondenza agli spigoli di
assorbimento a quelle energia capaci di ionizzare le shell interne dell’atomo,
vedi fig. 12
12
0.2. Produzione e rilevazione dei Raggi X
Figura 12: Andamento del coefficiente di assorbimento di massa vs. λ per il
Platino, con evidenziati gli spigoli di assorbimento K ed L
— Monocromatizzazione. In molti lavori di diffrazione si richiede la monocromatizzazione della radiazione incidente. Ovvero dallo spettro tipico di
un dato bersaglio si deve selezionara un preciso valore di lunghezza d’onda, tipicamente la riga Kα . Questo viene fatto nella maggior parte dei casi
con la tecnica del filtraggio, sfruttando l’andamento caratteristico degli spigoli di assorbimento in opportuni materiali. Ad esempio, come si vede in
fig. 13, se la radiazione X prodotta con un bersaglio di Mobildeno viene filtrata facendole attraversare un opportuno spessore di Zirconio, solo la riga
a λ = 0.63Å riesce ad attraversare il filtro.
Quando è invece richiesta una elevata monocromaticità si ricorre ai cristalli monocromatori. La radiazione prodotta dal bersaglio viene fatta riflettere
alla Bragg dai piani di un opportuno cristallo in modo da separare in angolo
le varie componenti di λ, anche se con notevole perdita di intensita.
Figura 13: Curva di assorbimento dello Zirconio, sovrapposta all radiazione
del Mobildeno
13
0.3. Diffrazione di raggi X da strutture cristalline
0.3 Diffrazione di raggi X da strutture cristalline
Come è stato detto lo studio delle strutture cristalline si attua principalmente attraverso la diffrazione di raggi X. Questo è il processo in cui un fascio di
fotoni X, incidente su un campione (cristallo singolo, policristallo o polvere policristallina), viene diffuso dagli elettroni di quest’ultimo (processo di
scattering). Dallo studio della distribuzione angolare della radiazione diffratta si risale alla forma, dimensione ed orientazione della cella elementare.
E’ inoltre possibile determinare le componenti (fasi) in una miscela di policristalli.
— Geometria della diffrazione
Da un punto di vista classico gli elettroni del materiale investito dal campo della radiazione elettro-magnetica dei raggi X sono forzati da questo ad
oscillare alla sua stessa frequenza, diventando così sorgenti secondarie di radiazione X. In questo processo vi è una precisa relazione di fase tra il campo
incidente e quello diffuso e lo scattering è detto essere coerente.
I fronti d’onda irradiati da tutti gli elettroni in un atomo si compongono
per formare una nuova sorgente elementare di diffusione, che può essere
Figura 14: Principio di Huygens.
considerata quasi puntiforme. Il campo così generato si somma a quello di
tutti gli altri atomi componenti il sistema e a causa della spaziatura regolare
tra le sorgenti elementari di diffusione si avranno fenomeni di interferenza
costruttiva o distruttiva dipendendo dall’angolo di osservazione del fascio
diffratto. Nella figura 15 è mostrata la differenza di cammino tra due centri di diffusione contigui. A seconda della relazione di fase nei due differenti percorsi si avranno, nella direzioni di osservazione, fenomeni di interferenza che consistono nell’aumento diminuizione o totale cancellazione
dell’intensità.
Nel caso di una distribuzione lineare regolare di atomi l’interferenza sarà
costruttiva per quelle direzioni in cui la differenza di fase tra i fronti diffusi da due atomi consecutivi e pari a nλ, dove n è un intero che definisce
l’ordine di diffrazione.
14
0.3. Diffrazione di raggi X da strutture cristalline
Figura 15: Differenza di cammino tra i raggi diffratti da due centri di
diffusione contigui.
— Condizioni di diffrazione da un reticolo tridimensionale
Per trattare il caso più generale di reticolo cubico, consideriamo dapprima
un reticolo lineare con spaziatura a0 . Siano ∆ e * gli angoli ripettivamente
formati dal reticolo con la direzione del fascio X incidente e la direzione di
osservazione, come in figura 16.
Figura 16: Condizioni di diffrazione per una schiera lineare di atomi.
Affinchè nella direzione di * ci sia interferenza costruttiva deve essere
OA − BP = mλ ovvero:
a0 (cos * − cos ∆) = mλ
da cui si può ricavare la direzione dell m-esimo ordine di diffrazione:
cos * = cos ∆ +
mλ
a0
15
0.3. Diffrazione di raggi X da strutture cristalline
Per un dato valore di a0 e di λ solo alcuni valori di m (intero) rendono possibile la soluzione di tale equazione per *. Inoltre, data la simmetria dell’angolo * rispetto la direzione della schiera lineare, le soluzioni dell’equazione
generano dei coni intorno a tale direzione.
Per generalizzare al reticolo cubico dobbiamo considerare gli angoli formati dalla direzione del fascio incidente con i tre assi del reticolo: ∆1 , ∆2 , ∆3 ,
e dalla direzione del fascio diffratto con gli stessi tre assi: *1 , *2 , *3 ; vedi
figura 17.
Figura 17: Condizioni di diffrazione per un reticolo cubico semplice.
ni:
In questo caso dovranno essere verificate simultaneamente le tre relazioa0 (cos *1 − cos ∆1 ) = mλ
a0 (cos *2 − cos ∆2 ) = pλ
a0 (cos *3 − cos ∆3 ) = qλ
Le espressioni sopra scritte sono note come condizioni di Laue e gli interi
m, p, q sono gli ordini di diffrazione dai tre reticoli lineari lungo gli assi OX,
OY e OZ.
I tre coseni di ∆ e di * non sono altro che i coseni direttori per le direzioni del
fascio incidente e del fascio difratto rispettivamente. Una formulazione più
istruttiva delle condizioni di Laue si ottiene considerando l’angolo formato
16
0.3. Diffrazione di raggi X da strutture cristalline
dalla direzione del fascio incidente con quello diffratto. Per convenzione
tale angolo si indica con 2θ e vale:
cos 2θ = (cos *1 · cos ∆1 + cos *2 · cos ∆2 + cos *3 · cos ∆3 )
Quadrando e sommando le tre condizioni di Laue si ottiene:
2a0
λ= !
sin θ
m2 + p2 + q 2
che lega l’angolo di diffrazione alle traslazioni primitive del reticolo (a0 ). O
anche, se m, p, q hanno un massimo comun divisore m = n·m0 , p = n·p0 , q =
n · q0 , si ha:
2a0
nλ = ! 2
sin θ
m0 + p20 + q02
Dove n rappresenta l’ordine di diffrazione. Una volta scritte le condizioni
di Laue in termini di θ conviene rappresentare la geometria di diffrazione
nel piano formato dal fascio incidente e dal fascio diffratto, come illustrato
in figura 18. .
Figura 18: Relazione tra il fascio incidente, il fascio diffratto e il piano di
riflessione..
Come si vede il fascio incidente appare come riflesso specularmente da
un piano perpendicolare al piano di diffrazione e che lo interseca sulla retta
RR" . Bragg ha dimostrato (1913) che tale piano di riflessione coincide con un
piano reticolare del cristallo i cui indici di Miller (hkl) sono proprio m0 , p0 , q0
e possiamo scrivere:
2a0
sin θ
nλ = √
h2 + k 2 + l2
ed identificare ogni raggio diffratto come una riflessione da una famiglia di
piani reticolari identificati dagli indici di Miller.
17
0.3. Diffrazione di raggi X da strutture cristalline
18
0
Inoltre per il caso considerato di sistema cubico si vede che il termine √h2 2a
+k2 +l2
rappresenta la distanza interplanare d tra i piani reticolari con indici (hkl).
Possiamo quindi scrivere in forma compatta:
nλ = 2d sin θ
nota come equazione o legge di Bragg che, anche se è stata ottenuta nel caso
del reticolo dubico, è di carattere del tutto generale.
Un’altra maniera di ricavare l’equazione di Bragg si ottiene considerando direttamente le riflessioni del fascio incidente da parte di una serie di
piani del cristallo con spaziatura d. Con riferimento alla figura 19. siano
Figura 19: Riflessione della radiazione incidente sui piani reticolari.
p, p1 , p2 etc. le tracce dei piani reticolari e θ l’angolo da questi formato rispettivamente con il fascio incidente e con quello riflesso. Affinchè nella
direzione di D ci sia interferenza costruttiva deve essere
B " C − BC = nλ
dato che:
B"C =
d
sin θ
e
BC = B " C cos 2θ =
(d cos 2θ)
sin θ
si ottiene:
d
d
(1 − cos 2θ) =
(2 sin2 θ) = nλ
sin θ
sin θ
da cui la legge di Bragg:
2d sin θ = nλ
che mostra nuovamente che per una data spaziatura d e lunghezza d’onda
λ i vari ordini di riflessione n si realizzano solo per precisi valori dell’angolo
0.3. Diffrazione di raggi X da strutture cristalline
θ che soddisfa la legge di Bragg, nelle altre direzioni l’interferenza annulla
la riflessione.
Un’altra interessante considerazione che deriva dalla legge di Bragg può
essere fatta descrivendo l’interazione tra radiazione e materia in termini dei
vettori d’onda della radiazione incidente e diffratta e dei vettori del reticolo reciproco. Come mostrato in figura 20 il fascio incidente può essere descritto in dal
Figura 20: Geometria di scattering in termini di momento scambiato.
suo vettore d’onda $k che ha la direzione della radiazione incidente e modulo
2π/λ. Il vettore d’onda del fascio diffratto ha lo stesso modulo, dato che non
vi è variazione di lunghezza d’onda, ma solo diversa direzione, formando
con il primo un angolo 2θ. La variazione di direzione corrisponde ad una
$ = !($ki − $kf ), perpendicolare ai piano reticolari e
variazione di momento !Q
di modulo pari a:
4π
!Q = 2!k sin θ = ! sin θ
λ
e facendo uso dell’equazione di Bragg si ha:
!Q = n
2π
!
d
che ricordando la definizione di vettori di reticolo reciproco mostra che si ha
diffrazione solo se il momento scambiato tra la radiazione incidente ed il sistema è
esattamente uguale ad uno dei momenti disponibili per il sistema, definiti proprio
dai suoi vettori di reticolo reciproco.
— La Sfera di Edwald
Gli angoli 2θ permessi con una data lunghezza d’onda e un certo angolo di
19
0.3. Diffrazione di raggi X da strutture cristalline
incidenza possono essere ottenute facilmente analizzando l’evendo di diffusione nel reticolo reciproco. Consideriamo nello spazio reciproco con origine in O , vedi figura 21, il vettore OA, corrispondente al vettore d’onda della
Figura 21: Costruzione di Edwald nello spazio reciproco.
radiazione incidente $k = 2π/λ. Con centro in A disegnamo la circonferenza
di raggio k; i punti del reticolo reciproco che cadranno sulla circonferenza
tracciata sono quelli che daranno luogo alle riflessioni e forniscono la direzione dei raggi diffratti, come ad esempio OB oppure OB " . I corrispondenti
piani nello spazio diretto sono quelli i cui indici di Miller coincidono con le
terna che individua il vettore OB o OB " .
In definitiva la distribuzione angolare dell’intensità della radiazione X
diffusa, in termini di direzione e modulo del momento scambiato Q, permette di ricostruire il reticolo reciproco e dalla inversione di questo si ottiene direttamente il reticolo spaziale. Le informazioni circa la struttura degli
atomi/molecole che formano la base è invece contenuta nella intensità dei
picchi di diffrazione, in particolare nel Fattore di Struttura di cui tratteremo
nella prossima sezione. Ovviamente le condizioni sperimentali quali monocromaticità, intensità, divergenza della radiazione incidente, accuratezza
nella misura degli angoli, limitatezza del range di momento scambiato, purezza dei campioni e così via, sarranno fattori limitanti nell’accuratezza con
cui può essere ricostruita la struttura del reticolo cristallino reale.
Prima di procedere all’analisi dei fattori che influenzano l’intensità della
diffusione consideriamo rapidamente i più comuni strumenti e metodi per
la diffrazione.
La strumentazione necessaria alla realizzazione di una misura di diffrazione X consiste, in linea di massima, dei seguenti elementi:
20
0.3. Diffrazione di raggi X da strutture cristalline
Sorgente di raggi X Tipicamente1 un moderno tubo radiogeno (eventualmete ad anodo rotante), dotato di un sistema monocromatizzazione e
di un insieme di fenditure per la collimazione del fascio.
Alloggiamento campione Una opportuno portacampione dotato di un sistema di posizionamento e/o orientazione, comprendente eventualmente la possibilità di modificare alcuni parametri della misura, quali
temperatura, pressione, campo magnetico e/o elettrico e via dicendo.
Sistema di rivelazione Un dispositivo sensibile alla radiazione X corredato
di un opportuno sistema di registrazione del segnale. Storicamente le
prime registrazioni venivano fatte su lastre fotografiche, protette dalla
radiazione visibile, che al termine della misura venivano poi sviluppate; di fatto, anche al giorno d’oggi, questo metodo viene ancora utilizzato. Sono anche in uso dei tubi fotomoltiplicatori, sensibili nel visibile, previa conversione della radiazione X tramite dei materiali detti
scintillatori2 ; in questo caso viene registrato il conteggio dei fotoni X in
funzione dell’angolo in cui è posizionato il detector. Più recentemente si fà uso di detector bidimensionali realizzati tramite camere CCD,
analoghe a quelli presenti nelle telecamere digitali; in questi sistemi
l’immagine viene direttamente registrata in formato digitale.
I vari metodi di diffrazione sono tutti finalizzati a registrare il maggior numero di riflessioni infatti la probabilità di rivelare una riflessione è generalmente bassa. Nel caso ideale di un cristallo perfetto e di una infinita precisione nella determinazione dei vettori d’onda incidente e diffuso, i punti
del reticolo reciproco sono di dimensione zero e la sfera di Ewald sarà una
superficie di spessore nullo.
Nel metodo di von Laue, un pennello di radiazione X, con uno spettro
continuo di lunghezze d’onda, incide su un monocristallo, come in figura 22. Il cristallo seleziona le lunghezze d’onda per cui esistono piani con
spaziatura d e angoli di incidenza che soddisfino alla relazione di Bragg. Il
pattern di diffrazione così ottenuto rappresenta una proiezione su un piano di tutti i punti del reticolo reciproco che cadono all’interno delle sfere di
Ewald relative al λmin e λmax . Il metodo si rivela utile per determinare con
rapidità l’orientazione del cristallo e la sua simmetria oltre che per studiare
le imperfezioni dei cristalli indotte da trattamenti termici o meccanici.
1
Presso le facility internazionali di luce di sincrotrone sono disponibili sorgenti di raggi
X estremamente intense e altamente collimate e monocromatiche. L’accesso a tali sorgenti
è regolato opportuni protocolli di collaborazionie scientifica internazionalie.
2
Questi materiali assorbono un quanto di radiazione X e tramite processi di fluorescenza emettono un quanto di radiazione nel visibile, in tempi dell’ordine di 10−8 ÷
10−9 secondi.
21
0.3. Diffrazione di raggi X da strutture cristalline
Figura 22: Sezione in due dimensioni del metodo di Laue ed esempio di
diffrattogramma.
Nel metodo del cristallo rotante, un monocristallo viene fatto ruotare intorno ad un asse mentre un fascio monocromatico di raggi X incide su di
esso. La variazione dell’angolo Ω porta differenti piani nelle condizioni di
riflessione, ovvero porta gli equivalenti punti nel reticolo reciproco ad attraversare la sfera di Ewald, vedi figura 23. . Il campione è ovviamente
Figura 23: Metodo del cristallo rotante e relativo diffrattogramma.
allogiato in un accurato sistema goniometrico che lo ruota intorno a due o a
tre assi e ne registra l’orientazione.
Nel metodo delle polveri, un fascio di raggi X monocromatico incide su
un campione in polvere o policristallino, formato dunque da un infinità di
microcristalli con tutte le possibili orientazioni. I raggi vengono diffratti
da quei singoli cristalli che si trovano nella giusta orientazione per soddisfare alla legge di Bragg. Nella diffrazione da polveri, a causa della simmetria nella distribuzione delle orientazioni dei microcristalli intorno alla
direzione del fascio incidente, i raggi diffratti diventano dei coni con cen-
22
0.4. Intensità della diffusione
tro nell’origine ed asse nella direzione del fascio incidente, detti coni di
Debye-Scherrer, vedi figura 24.
Figura 24: Coni di Debye-Scherrer e relativo diffrattogramma.
0.4 Intensità della diffusione
L’effettiva intensità relativa dei vari picchi di diffrazione dipende da vari
fattori che sono legati all’interazione radiazione-materia. Alcuni di questi
sono essenzialmente legati alla geometria della diffrazione mentre altri sono
legati ai vari livelli della struttura in cui sono organizzati i centri elementari
di diffusione ovvero gli elettroni.
0.4.1
Fattori geometrici
— Il fattore di polarizzazione.
Il fascio di raggi X incidente è in genere non polarizzato, ovvero il campo
EM oscilla in tutte le direzioni perpendicolari alla direzione di propagazione, con una distribuzione casuale. Nell’interazione con gli elettroni conviene scomporre la polarizzazione istantanea incidente in due componenti tra
loro ortogonali, una nel piano di scattering l’altra perpendicolare a questo.
Vedi figura 25. . Gli elettroni oscillano lungo queste due direzioni e riemettono radiazione EM, ma mentre per la componente perpendicolare al piano
di scattering l’intensità diffusa nella direzione del fasco diffratto è costante
(tale direzione è sempre perpedicolare alla direzione del moto oscillatorio),
per la componente parallela al piano di scattering l’intensità varia con il coseno dell’angolo di diffrazione (l’elettrone non irradia nella direzione del
proprio moto oscillatorio). In una radiazione non polarizzata due qualunque direzioni di polazizzazione tra loro perpendicolari sono presenti con
23
0.4. Intensità della diffusione
Figura 25: Polarizzazione della radiazione X diffratta.
uguale peso (50% ciascuna), cosicchè l’intensità in funzione di θ è data da:
I ∝ 21 (1 + cos2 θ).
— Il fattore di Lorentz.
Questo termine tiene conto di diversi fattori che hanno luogo nel caso di un
reale esperimento. Tali sono: la non perfetta monocromaticità della radiazione incidente, la leggera divergenza inerente al fascio incidente e diffratto,
la diversa orientazione dei microcristalli nei campioni policristallini e in polvere o la velocità con cui viene attraversata la sfera di ewald nel metodo del
cristallo rotante. Tutti questi fattori contribuiscono ad una diversa efficienza
per i diversi punti di reticolo reciproco nel contribuire all’intensità diffusa.
La correzione introdotta, nel caso di polveri è: 1/(sin(θ) sin(2θ) mentre nel
caso del cristallo rotante 1/ sin(2θ).
— Il fattore di molteplicità . Nel fenomeno della diffrazione da un reticolo
accade che diversi piani reticolari diffondano un qualche ordine di diffrazione allo stesso valore di θ, in particolare nel caso di polveri o policristalli.
Infatti dalla legge
di Bragg 2d sin θ = nλ con (nel caso di sistema cubico)
√
2
d(hkl) = a0 / h + k 2 + l2 , diverse combinazioni degli indici di Miller realizzano la stessa spaziatura. Ad esempio: (111) e (1̄11̄) oppure (300) e (221)
e così via. L’intensità diffusa ad un dato angolo risulta così aumentata, di
una quantità che può essere calcolata a partire dalla particolare struttura
cristallina.
0.4.2
Fattori di forma
I centri di diffusione non sono in realtà puntiformi, come fin’ora supposti, ma hanno una struttura estesa nello spazio. Le varie parti di tale forma
danno luogo a effetti di interferenza che modulano l’intensità diffusa in fun-
24
0.4. Intensità della diffusione
zione di Q conducendo ad un decremento, in genere monotono, dell’intensità stessa, vedi fig.26. Di seguito descriveremo questi effetti per il singolo
Figura 26: Differenze di fase generate dalle diverse parti della distibuzione
elettronica.
elettrone, l’insieme di questi nell’atomo e l’insieme di atomi nella molecola.
— Il fattore di Debye-Waller
Questo, detto anche fattore di temperatura, tiene conto del moto di agitazione termica degli atomi, e quindi degli elettroni a questi legati. Gli elettroni quindi non possono essere considerati come diffusori puntiformi, ma
come distribuiti su una regione di spazio (eventualmente asimmetrica) proporzionale allo spostamento del centro di massa degli atomi nelle tre direzioni spaziali. Nel caso più generale (distribuzione isotropica e gaussiana del moto di agitazione termica) l’intensità risulta diminuita di un fattosinθ ed &u2 ' lo
re exp(−Q2 &u2 ' /3) dove Q è il vettore d’onda scambiato 4π
λ
scarto quadratico medio rispetto alla posizione di equilibrio. Nella figura
27 sono illustrati gli ellisoidi termici del SiO4 e lo spostamento quadratico
medio nel Kr in funzione della temperatura.
— Il fattore di Forma Atomico.
Nell’interazione con i raggi X anche gli atomi a maggior ragione non possono essere considerarti puntiformi dato che le loro dimensioni sono all’incirca dello stesso ordine di grandezza della lunghezza d’onda della radiazione incidente. Di conseguenza i fronti d’onda elementari diffusi dai diversi
elettroni, distribuiti intorno al nucleo dell’atomo, presenteranno differenze di fase generando interferenze che producono una ulteriore monotona
diminuzione dell’intensità diffusa in funzione di sin θ/λ, come mostrato in
figura 28. .
25
0.4. Intensità della diffusione
Figura 27: Ellisoidi termici del quarzo e &u2 ' nelle tre direzioni del Kripton
Figura 28: Ellisoidi termici del quarzo e &u2 ' nelle tre direzioni del Kripton
L’esatta formulazione della dipendenza da θ dell’intensità dipende dalla
forma del particolare atomo, forma che dipende anche al suo stato di legame
chimico. Questa può essere calcolata teoricamente con diversi metodi che
descrivono la densità elettronica dei nuclei (Hartee-Fock e Thomas-Fermi)
ed i risultati sono tabulati in letteratura.
— Il Fattore Struttura Intramolecolare.
Nel caso, piuttosto generale, che la base della struttura reticolare sia formata
da una molecola composta da diversi atomi, bisogna considerare anche gli
effetti di interferenza derivanti dalla distribuzione spaziale di questi. Questi effetti sono decisamente rilevanti dato che le distanze tra gli atomi nella
molecola son ben confrontabili con le distanze della struttura reticolare da
26
0.4. Intensità della diffusione
queste formata. Molto spesso è proprio il dato sulla posizione relativa degli
atomi nella base quella più interessante poichè fornisce dettagliate informazioni sulla struttura della molecola3 , non altrimenti ottenibili con altre
tecniche.
Gli effetti dovuti all’organizzazione della molecola appaiono, nell’intensità
diffusa, tramite il quadrato del cosidetto Fattore di Struttura. Questo consiste, in pratica, in una trasformata di fourier della densità elettronica ρ(x, y, z)
nella cella elementare. Per una particolare riflessione il Fattore di Struttura
è un numero complesso dato da:
Fh,k,l =
N
"
j=1
fj · exp [2πı (huj + kvj + lwj )]
dove fi rappresenta il fattore di forma dell i-esimo di N atomi, h, k, l sono
gli indice della riflessione mentre ui , vi , wi sono le coordinate dell’atomo
nella cella elementare. Possiamo in un certo senso dire che l’intensità di ciascuna riflessione porta l’informazione su una particolare componente della
transformata di fourier della densità elettronica, quella con vettore d’onda
pari al corrispondente vettore di reticolo reciproco della riflessione.
Dobbiamo inoltre osservare che alcuni casi i fenomeni di interferenza
nella cella elementare possono anche cancellare alcune riflessioni del reticolo diretto.4 Questa circostanza è molto utile in quanto permette di determinare rapidamente la struttura reticolare in base a sistematiche assenze di
alcune riflessioni nel pattern di diffrazione.
Il fatto che la quantità misurabile sperimentalmente sia il quadrato del
Fattore di Struttura impedisce una sua diretta inversione di fourier per ottenere la densità elettronica
1 "
Fh,k,l · exp [−2πı (hx + ky + lz)]
ρ(x, y, z) =
V h,k,l
questo fatto è noto come problema della fase, in quanto è proprio la fase
espressa dalla parte complessa del Fattore di Struttura che viene persa nel
processo di misura. Possiamo in effetti riscrivere l’espressione precedente
nella forma:
3
Questa informazione è fondamentale nello studio delle molecole complesse quali
polimeri e biomolecole.
4
Infatti considerando, ad esempio, il caso del reticolo cubico a facce centrate (fcc) formato da quattro atomi nelle posizioni (0, 0, 0), ( 12 , 12 , 0), ( 12 , 0, 12 ) e (0, 12 , 12 , ), si ottiene per il
fattore di struttura Fhkl = f [1+eπı(h+k) +eπı(h+l) +eπı(k+l) ] != 0 solo se h, k, l sono tutti pari
o tutti dispari. In modo analogo si ottiene per un reticolo a corpo centrato (bcc) Fhkl != 0
solo se (h + k + l) è pari.
27
0.4. Intensità della diffusione
ρ(x, y, z) =
1 "
|Fh,k,l | exp [−2πı (hx + ky + lz − αh,k,l )]
V h,k,l
che mostra come sia necessario determinare il termine αh,k,l , oltre al modulo
del fattore di struttura, per calcolare la densità elettronica. Il contributo alla
fase totale portato da ciascun atomo componente la molecola è legato alla
sua distanza dal piano reticolare coinvolto in una certa riflessione, come
illustrato nella fig.29 . Gli atomi posti sui piani reticolari infatti diffondono
Figura 29: Relazione tra ritardo di fase e distanza dal piano reticolare.
con fase zero, il ritardo di fase aumenta con la distanza dal piano fino a
valere 2π per una distanza pari alla spaziatura interplanare.
Data la grande importanza della conoscenza della struttura molecolare, il problema della ricostuzione della fase è stato affrontato con diversi
approcci, di cui illustreremo i principi generali. I primi tre di questi sono
applicabili a molecole non troppo grandi (fino ad un centinaio di atomi)
mentre i restanti sono applicati a molecole biologiche, come proteine o acidi
nucleici, formati da molte migliaia di atomi.
Tirare a indovinare La ricostruzione della densità elettronica comincia con
una stima della disposizione (angoli e distanze) degli atomi nella molecola basata su considerazioni generali sugli atomi che la constituiscono (lunghezze, orientazioni e numero dei legami). La transformata
di fourier di tale stima si confronta con il dato sperimentale e dalle
differenze e somiglianze tra i due si migliora la stima iniziale. Con
un processo iterativo e molta pazienza ci si avvicina sempre più alla
densità elettronica corretta.
28
0.4. Intensità della diffusione
Metodo di Patterson La trasformata di fourier del quadrato del fattore di
stuttura, che è la quantità misurata sperimentalmente, è chiamata funzione di Patterson e presenta interessanti proprietà. Si dimostra che
questa consiste nella densità elettronica convoluta con il suo inverso:
$ e fornisce una mappa di tutte le N 2 possibili distanze
ρ($r) ⊗ ρ(−r),
tra gli N atomi nella molecola. In tale mappa gli atomi più pesanti si
presentano con maggiore intensità, risulta così possibile valutare facilmente la posizione di questi e quindi risalire anche alla posizione di
quelli più leggeri.
Metodo diretto Questo si basa su proprietà matematiche del fattore di struttura, dovute alla periodicità del cristallo, per cui esistono relazioni statistiche tra la fase e l’intensità dei picchi. Valutando queste relazioni
su terne di picchi (tre riflessioni la cui intensità e fase di una è calcolata da quella delle restanti due è detta avere una relazione tripla) e
facendo uso di delle appropriate procedure matematiche si perviene
alla ricostruzione delle fasi delle riflessioni presenti.
Sostituzione molecolare Consiste nel costruire la densità elettronica partendo da una molecola simile a quella in esame, usata in particolare
per le proteine. Se due proteine hanno una sequenza simile al 40-50%
anche la loro struttura sarà molto simile. Si tratta quindi di trovare
la posizione e l’orientazione per la proteina nota nella cella, in modo
da riprodurre il più possibile il dato sperimentale relativo alla proteina incognita. Si riesce così a localizzare il maggior numero di atomi
rendendo facile la localizzazione di quelli restani.
Sostituzione multipla isomorfa L’idea è di perturbare parzialmente ed in
vari modi la struttura della macromolecola in esame in modo da modificarne il fattore di struttura, dalle variazioni osservate si fanno deduzioni sulle possibili fasi iniziali. In genere si aggiungono o sostituiscono atomi con altri ben più pesanti in modo che le differenze siano
più evidenti. Diventa anche possibile fare delle mappe differenza da
studiare con i metodi precedenti.
Dispersione anomala Concettualmente simile alla precedente ma in questo caso viene variata l’efficenza di diffusione degli atomi presenti
sfruttando la dispersione anomala. Questa consiste in una sostanziale
variazione dell’intensità diffusa a certe lunghezze d’onda, quelle con
energia prossima ad uno spigolo di assorbimento. Anche in questo
caso dalle modifiche del fattore di struttura con la lunghezza donda
usata si deducono informazioni sulla fase degli atomi in dispersione
29
0.5. Analisi quantitativa e qualitativa
anomala. Questa tecnica è forse la più efficace anche se necessita di
sorgenti a lunghezza d’onda variabile quali i sincrotroni.
0.5
Analisi quantitativa e qualitativa
— Analisi qualitativa. La possibilità di effettuare un analisi qualitativa tramite diffrazione a raggi X da polveri si basa sulle due seguenti considerazioni:
• ogni elemento o composto chimico capace di assumere forma cristallina da luogo ad una figura (pattern) di diffrazione differente da quello
di altre sostanze;
• in una miscela di differenti componenti cristallini ciascun componente
da luogo al proprio pattern di diffrazione indipendante dagli altri.
Dei limiti sono ovviamente posti dalla possibilità di rilevare basse intensità delle riflessioni dovute a basse concentrazioni di materiale, e
dalla eccesiva complessità del pattern di diffrazione nel caso di un
troppo elevato numero di componenti presenti.
I vantaggi di tale tecnica sono la rapidità della misura e l’esigua quantità di
campione richiesto.
Di fatto per riconoscere la presenza di una data sostanza nella miscela si
confrontano i riflessi rilevati nei dati sperimentali con una lista contenente
l’insieme dei riflessi generati da ciascuna delle sostanze note. La lista più
usata è quella prodotta dall’American Society for Testing Materials, contenete circa 4000 voci, da cui deriva il nome assegnato a questa procedura;
ovvero metodo A.S.T.M.
Di seguito sono mostrate alcune di questa schede, in cui sono contenute informazioni circa la sostanza catalogata, le distanze reticolari, i relativi indici
di Miller e una scala relativa di intensità (da 1 a 100) per ciascuna riflessione.
Figura 21. Esempi di schede dell’American Society for Testing Materials.
– Analisi quantitativa. Dopo aver rilevato le sostanze presenti in un dato
campione tramite l’analisi qualitativa è possibile svolgere un analisi quantitativa per risalire alla concentrazione delle stesse. Questo viene fatto tramite
una valutazione dell’intensità delle riflessioni dovute a ciascuna specie confrontandola con opportuni standard. In tale analisi entra in gioco il fattore
di assorbimento che tiene conto della frazione di intensità che viene assorbita nell’attraversamento dei raggi X da parte del campione.
L’intensità dell’i-esimo riflesso di una miscela è dato (nella geometria BraggBentano) da:
1 xα 1
M L P |Fiα |2
Iiα = I0 A 2
2Vc ρα µM
30
0.5. Analisi quantitativa e qualitativa
31
I0 l’intensità del fascio incidente
A costante dello strumento
Vc volume della cella unitaria della fase α
xα frazione in peso della fase α
ρα densità della fase α
µM coefficiente di assorbimento di massa della miscela
M molteplicita del riflesso
L P fattore di Lorentz e di polarizzazione
Fiα Fattore di Struttura del riflesso.
Dei termini considerati, a parte la costante dello strumento e l’intensità del
fascio incidente, il coefficiente µM dipende dalla composizione dell’intera
miscela e i restanti dipendono solo dalla particolare fase presa in considerazione. Conviene perciò riscrivere l’espressione nella forma:
Iiα = Kiα
xα 1
ρα µM
dove Kiα comprende sia la parte strumentale che le caratteristiche proprie
dell’i-esimo riflesso della componente α.
Questa espressione è alla base dell’analisi qualitativa. Difatti se conosciamo
quale sia la componente α, e dunque la sua densità ed il suo coefficiente di
assorbimento, possiamo valutare il termine Kiα da una misura dell’i-esimo
riflesso nel componente puro xα = 1 ed utilizzarla per calcolarne la sua
frazione nella miscela. Questo però a patto di conoscere il coefficente di assorbimento della miscela che può essere ricavato da misure di trasmissione
sulla miscela. Tale procedura è definita come metodo del componente noto.
Un altro sistema più spesso utilizzato è il metodo dello standard interno.
Questo metodo consiste nell’aggiungere alla miscela in questione una determinata frazione x0 di un altro componente, ovviamente noto. In tale caso
"
si misurano le intensità dell’i-esimo riflesso per il componente α: Iiα
, ed il
j-esimo riflesso per il componente noto: Ij0 . Nel rapporto tra le due quantità
viene eliminato il termine legato al coefficente di assorbimento; che ora si
riferisce alla nuova miscela. Possiamo dunque scrivere:
"
Kiα x"α ρ0
xα
Iiα
=
= K"
Ij0
Kj0 x0 ρα
x0
0.5. Analisi quantitativa e qualitativa
con ovvio significato del termine K " che si riferisce solo alle densità dei due
componenti in questione ed alle caratteristiche dei loro riflessi selezionati e
non dipende dalla costante dello strumento.
Il termine K " viene valutato preparando una terza miscela composta solo
dal componente α e dal componente noto. Su questa terza miscela si ripetono le misure dell’intensità dei riflessi considerati, e dato che le frazioni in
peso sono ora note si risale al valore di K " .
Questo chiaramente permette di ottenere la frazione in peso della componente α per la seconda miscela x"α che è legata alla relativa frazione nella
miscela originaria dalla relazione:
xα =
x"α
1 − x0
Procedendo allo stesso modo per tutte le componenti si determina infine
l’esatta composizione della miscela in studio.
32