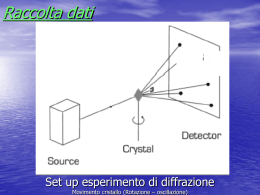
Interazione dei raggi X con la materia
Emissione di fotoelettroni
Fluorescenza
Fascio incidente (I0)
di raggi X
Scattering coerente e incoerente
Assorbimento (I)
calore
Lo scattering coerente dei raggi X è responsabile degli effetti di diffrazione
Gli elettroni diventano sorgenti secondarie di radiazione X
avente la stessa λ della radiazione incidente
Il fenomeno della diffrazione
La diffrazione è un complesso fenomeno di diffusione (o scattering) e
interferenza originato dall’interazione di onde elettromagnetiche (raggi X) o
particelle “relativistiche” (neutroni e elettroni) aventi appropriata lunghezza
d’onda (dell’ordine dell’Å) con un reticolo cristallino.
Il processo di diffusione (o scattering)
L’interazione di un’onda elettromagnetica con la materia avviene essenzialmente
attraverso due processi di scattering che riflettono il dualismo onda-particella
della radiazione incidente:
a) scattering elastico: i fotoni della radiazione incidente vengono deviati
in ogni direzione dello spazio senza perdita di energia. Esiste dunque una
precisa relazione fra radiazione incidente e radiazione diffusa per cui il
processo viene definito coerente. Questo processo è alla base della
diffrazione.
b) scattering non-elastico: il fotone cede parte della sua energia; la
radiazione diffusa risultante ha quindi lunghezza d’onda maggiore di
quella incidente. Non essendoci alcuna relazione fra radiazione incidente
e radiazione diffusa, questo tipo di scattering è definito incoerente.
Questo fenomeno non dà luogo a processi di interferenza.
Interazione raggi X con:
Una singola particella
La particella diffonde il
fascio incidente
uniformemente in tutte le
direzioni
Un materiale cristallino
I fasci diffusi si combinano
construttivamente in certe
direzioni
λ/2
Interferenza Costruttiva
Interferenza distruttiva
Scattering di RX
Il fenomeno della diffrazione è analogo all’interferenza
della luce con un reticolo ottico.
Lungo alcune direzioni (direzione 3) i fasci diffratti A e B
si trovano esattamente sfasati di mezza lunghezza d’onda:
si ha interferenza distruttiva e lungo la direzione 3 si avrà
intensità nulla.
Lungo le direzioni 1 e 2 i due fasci sono in fase e avremo
un massimo di intensità lungo quelle direzioni.
Tra le direzioni 1 e 2 avremo tutte le
gradazioni intermedie.
Se però considero un reticolo ottico devo
considerare non solo 2 fasci ma milioni,
questo fa si che si abbia una grande
intensità esattamente per le direzioni 1 e
2 e intensità praticamente nulla per tutte
le altre.
Condizioni di Laue
Max von Laue interpretò la diffrazione di raggi X da parte dei cristalli considerando che la
disposizione periodica tridimensionale degli atomi corrisponde a un reticolo tridimensionale
di diffrazione
(analogia con la diffrazione della luce da parte di un reticolo ottico)
Partiamo da un reticolo monodimensionale costituito da un atomo situato nei nodi reticolari
che agiscono come centri di scattering
Radiazione S0 incide con angolo di incidenza φ
su un filare monodimensionale.
Radiazione diffratta S forma un angolo θ con
il fascio incidente
Interferenza è costruttiva solo se la differenza di cammino ottico dei raggi
scatterati da due contigui è pari a un multiplo della lunghezza d’onda
Differenza di cammino sul raggio incidente (r), e sul raggio
diffratto (r').
r' - r = a cos(θ) - a cos (φ) = h λ
h numero intero.
In termini vettoriali:
r' - r = a · (S-S0) = h λ
I raggi diffratti giacciono su coni, detti di Laue,
associati ai diversi valori di h.
Il cristallo (e il relativo reticolo) è tridimensionale
dobbiamo scrivere relazioni analoghe per le altre due direzioni
Condizioni di Laue per la diffrazione:
a . (S-S0) = h λ
b . (S-S0) = k λ
c . (S-S0) = l λ
Le tre equazioni di Laue devono essere contemporaneamente soddisfatte,
la diffrazione avviene solo lungo le direzioni comuni a tre superfici coniche.
L’approccio di Laue seppure corretto è poco pratico (tre equazioni devono
essere soddisfatte contemporaneamente).
Bragg (padre e figlio) immaginarono il fenomeno in termini di riflessione dei
raggi X da parte di piani reticolare infinitamente estesi.
Approccio dei Bragg non è corretto dal punto di vista fisico (il vero fenomeno
che avviene è la diffusione e l’interferenza tra onde diffuse) ma fornisce una
espressione semplice (una unica equazione) e del tutto equivalente alle tre
condizioni di Laue (la direzione del fascio riflesso della legge di Bragg concide
con la direzione che soddisfa contemporaneamente le 3 equazioni di Laue)
Nell’approccio di Bragg i piani reticolari sono immaginati essere semiriflettenti
I raggi X incidono su un pianoe vengono in parte riflessi, in parte trasmessi
La riflessione avviene anche sui piani sottostanti
Interferenza è costruttiva solo se la differenza di cammino tra i raggi riflessi
da piani contigui è pari a un multiplo della lunghezza d’onda
r + r = dhkl sin(θ) + dhkl sin(θ) = n λ
2dhkl sin(θ) = n λ
Legge di Bragg
2dnh nk nl sin(θ) = λ
N.B. La direzione dei fascio diffratto prevista dalle tre condizioni di Laue coincide
con quella prevista dalla legge di Bragg
2d sinθ = λ
d = distanza interplanare
La direzione dei raggi diffratti dipende UNICAMENTE dal reticolo di
traslazione, cioè dai parametri della cella elementare,
indipendentemente dagli atomi che essa contiene
PROPORZIONALITÀ INVERSA TRA sinθ e d
strutture con d grandi mostreranno pattern di diffrazione compressi,
e viceversa per strutture con d piccoli
1/d = (2/λ) sinθ
1/d ∝ sinθ
Il pattern di diffrazione è una immagine del reticolo reciproco
Interpretazione in termini vettoriali della legge di Bragg
Il vettore differenza (S-S0) tra il vettore unitario sulla direzione dell'onda incidente
(S0) e quello sull’onda diffratta (S) è parallelo al vettore del reticolo reciproco d*hkl.
|S-S0|= 2 sin(θ)
|d*hkl| = 1/dhkl
λ = 2dhkl sin(θ) = |S-S0| / | d*hkl |
Da cui si può scrivere la legge di Bragg come:
(S-S0) / λ = d*hkl = ha* + kb* + lc*
Quando la legge di Bragg è soddisfatta il vettore (S-S0) / λ coincide con il
vettore del reticolo reciproco dei piani che sono in condizioni di riflessione
Interpretazione di Ewald
Sintesi "geometrica" delle condizioni di diffrazione (ci fa capire come
effettuare un esperimento di diffrazione)
Ewald suggerì di costruire una sfera (sfera di Ewald) di raggio 1/λ
con il cristallo (reticolo diretto) al centro
L'origine del reticolo reciproco è fissata nell'intersezione tra la sfera ed il
prolungamento del vettore S0.
il punto di intersezione tra la sfera e il vettore S è un punto del reticolo
reciproco
Un piano hkl si trova in condizioni di diffrazione se il corrispondente vettore
del reticolo reciproco giace sulla superficie della sfera di Ewald
Alcuni punti si trovano sulla sfera
Come possono essere osservate le
diffrazioni di altri piani?
Possiamo immaginare due "metodi":
•ruotare il reticolo reale (quindi il cristallo)
mantenendo costante λ (Metodo di Bragg)
•modificare il raggio della sfera di Ewald
(quindi la lunghezza dell'onda incidente) in
modo che altri nodi siano toccati dalla sfera
(metodo di Laue).
Esercizio
Un cristallo di Fe (bcc a=2.866 Å) viene sottoposto a un esperimento di
diffrazione di Raggi X utilizzando la radiazione Cr Kα (λ=2.291 Å)
•Calcolare i valori delle distanze interplanari dhkl
•Calcolare gli angoli di Bragg (N.B. in effetti si osservano solo riflessi
con h+k+l=2n)
•Calcolare gli angoli di Bragg usando la radiazione Mo Kα (λ=0.7107 Å)