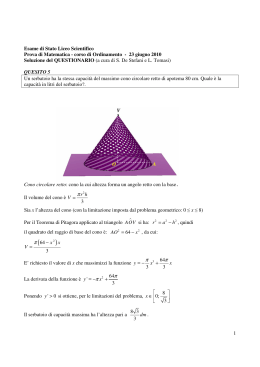
LEZIONE 37
37.1. Altri esempi di superfici.
In questo paragrafo daremo altri esempi di superfici.
Esempio 37.1.1. Sia D ⊆ R2 un aperto. Allora il grafico Γϕ di una funzione ϕ: D → R3
di classe C 1 è una superficie regolare. Infatti la parametrizzazione f (u, v) = (u, v, ϕ(u, v))
è iniettiva (attenzione, come per le curve, si richiede l’iniettività di f , non di ϕ). Inoltre


1
0

Jf(u0 ,v0 ) = 
0
1
∂ϕ
∂ϕ
∂u (u0 , v0 )
∂v (u0 , v0 )
ha sempre, evidentemente, rango 2.
Per esempio siano a, b > 0 e si considerino il paraboloide ellittico e quello iperbolico di
semiassi a, b, rispettivamente di equazioni
x2
y2
+
= 2z,
a2
b2
x2
y2
−
= 2z.
a2
b2
Esempio 37.1.2. Sia S il cilindro luogo dei punti P = (x, y, z) soddisfacenti l’equazione
(37.1.2.1)
x2 + y 2 = %2 .
Sia Pxy la proiezione ortogonale del punto P sul piano xy. Indichiamo con u l’angolo
~ xy . Indichiamo con v la quota del punto P (si veda la Figura 37.1).
formato da ~ı e OP
Chiaramente
P = (% cos u, % sin u, v).
In particolare S è immagine dell’applicazione
f : R2 −→ R3
(u, v) −→ (% cos u, % sin u, v).
In tal caso abbiamo

Jf(u0 ,v0 )
−% sin u0
=  % cos u0
0

0
0.
1
Typeset by AMS-TEX
1
2
37.1. ALTRI ESEMPI DI SUPERFICI
Si noti che tale matrice ha sempre rango 2.
z
S
v
P
O
u
y
ρ
Pxy
x
Figura 37.1
Il cilindro considerato è un caso particolare di cilindro proiettante una curva nel senso
della costruzione seguente. Sia g = (gx , gy , gz ): I → C ⊆ R3 una qualsiasi curva parametrizzata e p~ = px~ı + py~ + pz~k un vettore non nullo. Si consideri
f : R ×I −→ R3
(u, v) −→ (gx (u) + px v, gy (u) + py v, gz (u) + pz v).
La superficie Cil(C, w)
~ = im(f ) viene detta cilindro proiettante C secondo la direzione di
p~. Risulta

 dgx
du (u0 ) px
y
:
Jf(u0 ,v0 ) =  dg
du (u0 ) py
dgz
du (u0 ) pz
in particolare, se g è una parametrizzazione regolare di C, la superficie parametrizzata f è
regolare in P0 = f (u0 , v0 ) se e solo se la retta tangente a C in Q0 = g(u0 ) non è parallela
al vettore p~.
Si noti che, essendo
(% cos u, % sin u, v) = (% cos u, % sin u, 0) + (0, 0, 1)v,
il cilindro d’Equazione (37.1.2.1) è esattamente il cilindro proiettante la circonferenza di
centro (0, 0, 0) e raggio % contenuta nel piano xy secondo la direzione di ~k .
Chiaramente se C è piana e p~ è parallelo al piano di C, tale superficie è esattamente una
regione non limitata del piano di C. Se p~ non è parallelo all’eventuale piano contenente C
(se ne esiste uno), allora Cil(C, p~) è regolare se e solo se la curva C lo è.
Come ultimo esempio si consideri la cubica sghemba C di equazioni (x, y, z) = (t, t2 , t3 )
definita nella Lezione 13. Sia p~ = ~ı + ~ + ~k . Allora Cil(C, p~) ha equazioni parametriche
(x, y, z) = (u + v, u2 + v, u3 + v)
LEZIONE 37
3
Esempio 37.1.3. Sia S il cono luogo dei punti P = (x, y, z) soddisfacenti l’equazione
x2 + y 2 = z 2 .
(37.1.3.1)
~ e ~k è costantemente uguale a π/4. Sia Pxy la proiezione
Allora l’angolo formato da OP
~ xy .
ortogonale del punto P sul piano xy. Indichiamo con u l’angolo formato da ~ı e OP
Indichiamo poi con v la quota del punto P .
z
v
P
O
y
u
Pxy
x
Figura 37.2
Chiaramente S è immagine dell’applicazione
f : R2 −→ R3
(u, v) −→ (v cos u, v sin u, v).
In tal caso abbiamo

Jf(u0 ,v0 )
−v0 sin u0
=  v0 cos u0
0

cos u0
sin u0  .
1
Si noti che tale matrice ha rango 2 per v 6= 0.
Il cono considerato è un caso particolare di cono proiettante una curva nel senso della
costruzione seguente. Sia g = (gx , gy , gz ): I → C ⊆ R3 una qualsiasi curva parametrizzata
e A = (xA , yA , zA ) un punto. Si consideri
f : R ×I −→ R3
(u, v) −→ (xA + (gx (u) − xA )v, yA + (gy (u) − yA )v, zA + (gz (u) − zA )v).
La superficie Cono(C, A) = im(f ) viene detta cono proiettante C dal punto A e il punto A
si dice vertice del cono. Risulta

 dgx
v0 du (u0 ) gx (u0 ) − xA
y
Jf(u0 ,v0 ) =  v0 dg
gy (u0 ) − yA  :
du (u0 )
dgz
v0 du (u0 ) gz (u0 ) − zA
4
37.1. ALTRI ESEMPI DI SUPERFICI
in particolare la superficie parametrizzata f non è regolare per v0 = 0, cioè nel punto A.
Per esercizio determinare una condizione geometrica su A e C che permetta di descrivere il
luogo dei punti regolari della parametrizzazione f (almeno nell’ipotesi di regolarità di g).
Si noti che, essendo
(v cos u, v sin u, v) = (0, 0, 0) + (cos u, sin u, 1)v,
il cono avente Equazione (37.1.3.1) è esattamente il cono proiettante la circonferenza di
centro (0, 0, 1) e raggio 1 contenuta nel piano di equazione z = 1 dall’origine O.
Cosa accade se C è piana e se A appartiene al piano della curva?
Come ultimo esempio, si consideri, di nuovo, la cubica sghemba C di equazioni (x, y, z) =
(t, t2 , t3 ). Sia A = (1, 0, 1). Allora Cono(C, A) ha equazioni parametriche
(x, y, z) = (1 − v + uv, u2 v, 1 − v + u3 v)
Esempio 37.2.5. Un esempio di superfici interessanti sono quelle ottenute nel modo
seguente. Sia C ⊆ R3 non intersecante l’asse delle z: per ogni P ∈ C indichiamo con Pz la
sua proiezione ortogonale sull’asse z che, per ipotesi, è diversa da P . Consideriamo allora la
superficie Seg(C) unione di tutte le rette rP Pz passanti per P e Pz . Sia g = (gx , gy , gz ): I →
C ⊆ R3 è una parametrizzazione di C: se P = g(t), allora Pz = (0, 0, gz (t)), quindi una
parametrizzazione per Seg(C) è
(u, v) 7→ f (u, v) = (vgx (u), vgy (u), gz (u)),
con (u, v) ∈ I × R. Allora

x
v dg
du (u) gx (u)
y
.
=  v dg
du (u) gy (u)
dgz
0
du (u)

Jf(u,v)
Determinare l’insieme dei punti dove f non è regolare.
Per esempio sia C l’elica cilindrica di raggio % e passo h parametrizzata da g(t) =
(% cos t, % sin t, ht), t ∈ R. Allora Seg(C) viene detta elicoide di passo h. Una sua parametrizzazione è data da
(u, v) 7→ h(u, v) = (v% cos u, v% sin u, hu),
con (u, v) ∈ R2 . Si noti che sostituendo al parametro v il parametro v/% si ottiene una
nuova parametrizzazione dell’elicoide
(u, v) 7→ f (u, v) = (v cos u, v sin u, hu),
con (u, v) ∈ R2 , indipendente da %: ovvero l’elicoide dipende solo dal passo dell’elica
generatrice, non dal suo raggio.
LEZIONE 37
5
37.2. Il piano tangente a una superficie.
Ritorniamo ora sulla nozione di superficie regolare per introdurre la nozione di piano
tangente ad una superficie in un suo punto. Ricordiamo che dire che S è una superficie
regolare significa che esiste una sua parametrizzazione f : D → S che sia iniettiva, di classe
C 1 e tale che

 ∂fx
∂fx
∂u (u, v)
∂v (u, v)
∂fy
y

Jf(u,v) =  ∂f
∂u (u, v)
∂v (u, v)
∂fy
∂fy
∂u (u, v)
∂v (u, v)
su D. Dal punto di vista geometrio quest’ultima condizione significa che
∂f
(u, v),
∂u
∂f
(u, v),
∂v
pensati come vettori applicati, non sono mai paralleli.
Si fissi P0 ∈ S e sia (u0 , v0 ) ∈ D tale che f (u0 , v0 ) = P0 : d’ora innanzi supporremo che
la superficie S sia regolare in P0 . Se C ⊆ S è una curva regolare passante per P0 si può
vedere facilmente che esiste una funzione regolare g: I → D tale che F = f ◦ g: I → R3
sia una parametrizzazione regolare di C. Se F (t0 ) = P0 , allora g(t0 ) = (u0 , v0 ) e la retta
tangente TP0 (C) a C in P0 risulta essere parallela al vettore
∂f
dgu
∂f
dgv
dF
(t0 ) =
(u0 , v0 )
(t0 ) +
(u0 , v0 )
(t0 ) 6= 0.
dt
∂u
dt
∂v
dt
In particolare tale retta è perpendicolare al vettore
~ = ∂f (u0 , v0 ) × ∂f (u0 , v0 )
N
∂u
∂v
(che è non nullo per l’ipotesi sul rango della matrice jacobiana).
~ , quindi complanare
Viceversa consideriamo un qualsiasi vettore p~ perpendicolare a N
con i vettori
∂f
∂f
(u0 , v0 ),
(u0 , v0 ).
∂u
∂v
Allora esistono λu , λv ∈ R non contemporaneamente nulli e tali che
p~ = λu
Siano λ =
p
∂f
∂f
(u0 , v0 ) + λv (u0 , v0 ).
∂u
∂v
λ2u + λ2v e w = λ−1 (λu , λv ) allora
∂f
∂f
∂f
(u0 , v0 ).
p~ = λ wu (u0 , v0 ) + wv (u0 , v0 ) = λ
∂u
∂v
∂w
Consideriamo la funzione g: R → R2 definta da g(u0 +twu , v0 +twv ). La funzione F = f ◦g
è definita in un opportuno intorno sferico di (u0 , v0 ) e risulta
dF
∂f
∂f
∂f
(0) =
(u0 , v0 ) = wu (u0 , v0 ) + wv (u0 , v0 ).
dt
∂w
∂u
∂v
6
37.2. IL PIANO TANGENTE A UNA SUPERFICIE
~ in V3 (O)
Quanto detto sopra dà una motivazione del fatto che il sottospazio generato N
non dipende dalla parametrizzazione, ma solo dal punto P0 e dalla superficie, in quanto
contiene tutti i vettori perpendicolari alle rette tangenti a tutte le curve tracciate su S nel
punto P0 .
Per questo motivo diamo la seguente definizione
Definizione 37.2.1. Sia S una superficie regolare e f : D → R3 una sa parametrizzazione
regolare. Se P0 = f (u0 , v0 ) ∈ S, la retta NP0 (S) di equazione
∂f
∂f
(u0 , v0 ) ×
(u0 , v0 )
x = f (u0 , v0 ) + τ
∂u
∂v
τ ∈ R, viene detta retta normale a S nel punto P0 . Ogni vettore parallelo a NP0 (S) viene
detto vettore normale a S in P0 .
Il piano TP0 (S) passante per P0 e perpendicolare a NP0 (S) viene detto piano tangente
a S nel punto P0 .
Riprendiamo ora gli esempi in questa lezione ed in quella precedente e calcoliamo
l’equazione del piano tangente (e, quindi, della retta normale).
Per esercizio si verifichi che se π ⊆ R3 è un piano e P0 ∈ π, allora TP0 (π) = π.
Esempio 37.2.2. Si consideri la sfera S di centro l’origine e raggio % > 0. Ricordiamo (si
veda il Paragrafo 35.2.2) che una sua parametrizzazione è
(u, v) 7→ P = f (u, v) = (% cos u cos v, % sin u cos v, % sin v)
e che la corrispondente matrice jacobiana è

− sin u cos v
Jf(u,v) = %  cos u cos v
0

− cos u sin v
− sin u sin v  .
cos v
Dunque, quando v0 6= π/2 + kπ, k ∈ Z, un vettore normale a S in P0 = f (u0 , v0 ) è
(cos u0 cos v0 )~ı + (sin u0 cos v0 )~ + (sin v0 )~k .
Concludiamo che il piano tangente a S in un suo punto P 6= (0, 0, 1), (0, 0, −1), è il piano
~ . Cambiando parametrizzazione si osserva che vale
passante per P e perpendicolare a OP
una caratterizzazione analoga per il piano tangente a S nei punti (0, 0, 1) e (0, 0, −1).
Esempio 37.2.3. Sia D ⊆ R2 un aperto. Abbiamo visto nell’Esempio 37.1.1 come il
grafico Γϕ di ogni funzione ϕ: D → R3 di classe C 1 sia una superficie regolare. Se (u0 , v0 ) ∈
D, allora


1
0
,
Jf(u0 ,v0 ) = 
0
1
∂ϕ
∂ϕ
∂u (u0 , v0 )
∂v (u0 , v0 )
LEZIONE 37
7
sicché la retta normale NP0 (Γϕ ) a Γϕ nel punto P0 = (u0 , v0 , ϕ(u0 , v0 )) è parallela al
vettore.
∂ϕ
∂ϕ
(u0 , v0 )~ + ~k .
− (u0 , v0 )~ı −
∂u
∂v
In particolare il piano tangente TP0 (Γϕ ) a Γϕ in P0 ha equazione
−
∂ϕ
∂ϕ
(u0 , v0 )(x − u0 ) −
(u0 , v0 )(y − v0 ) + (z − ϕ(u0 , v0 )) = 0
∂u
∂v
o, esplicitando rispetto a z,
z = ϕ(u0 , v0 ) +
∂ϕ
∂ϕ
(u0 , v0 )(x − u0 ) +
(u0 , v0 )(y − v0 ).
∂u
∂v
Si noti che l’equazione di tale piano non è altro che la parte iniziale dello sviluppo di Taylor
della funzione ϕ di punto iniziale (u0 , v0 ).
Esempio 37.2.4. Si consideri il cilindro S dell’Esempio 37.1.2. Una sua parametrizzazione è
(u, v) 7→ P = f (u, v) = (% cos u, % sin u, v)
e che la corrispondente matrice jacobiana è

Jf(u,v)

−% sin u 0
=  % cos u 0  .
0
1
Dunque un vettore normale a S in P0 = f (u0 , v0 ) è
(cos u0 )~ı + (sin u0 )~ .
~ xy ove Pxy è la proiezione ortogonale di P0 sul piano xy:
Tale vettore è parallelo a OP
concludiamo che il piano tangente a S in un suo punto P0 , è il piano passante per P0 e
~ xy .
perpendicolare OP
Osservazione 37.2.5. Si consideri il cono Cono(C, A) proiettante la curva C dal punto
A. Abbiamo già determinato una parametrizzazione f di tale superficie in funzione
di una parametrizzazione g di C. Abbiamo anche visto che anche se C è regolare, la
parametrizzazione indotta f non è mai regolare in A.
In effetti si dimostra facilmente che la superficie Cono(C, A) stessa non è mai regolare
nel suo vertice. Infatti, se C non è piana, su Cono(C, A) giacciono tre rette passanti per A
e non complanari. Dunque non può esistere nessun piano contenente le rette tangenti in
A a tutte le curve tracciate su Cono(C, A), cosa che dovrebbe accadere se Cono(C, A) fosse
regolare.