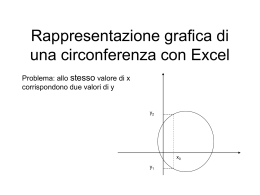
LICEO SCIENTIFICO “VITTORIO VENETO” - MILANO
SCHEDA DI LAVORO n° 1 - La cicloide come traccia
La cicloide è raffigurata dalla curva in rosso, che rappresenta la traccia del punto P appartenente alla circonferenza, che ruota in senso orario.
La cicloide è la curva descritta da un punto
che appartiene alla circonferenza di un cerchio che rotola, senza strisciare, su una retta,
detta direttrice.
Costruiamo la cicloide con l’aiuto di CABRI.
Modifica le preferenze per i luoghi: nel menu
OPZIONI/PREFERENZE apri la scheda OPZIONI
All’origine del moto P=M=O; la distanza OM sulla semiretta s è uguale alla misura dell’arco MP.
PER I LUOGHI ed imposta a 500 il numero di
1. Rappresenta il punto O, la semiretta Os, un segmento AB che vuole essere il raggio della circonferenza e
sia M un punto sulla semiretta. Misura il segmento OM
Ricorda che, se vuoi ottenere delle linee oriz-
2. Costruisci la circonferenza di raggio AB e tangente in
M alla semiretta Os: quali passi devi seguire?
Le circonferenze in CABRI possono essere
punti di un luogo
zontali, devi tenere premuto il tasto MAIUSC
mentre le tracci
tracciate sia usando il comando CIRCONFERENZA che usando il comando COMPASSO
3. Usando TRASPORTO DI MISURA, riporta la distanza OM
sulla circonferenza: per farlo devi indicare nell’ordine
la circonferenza su cui vuoi trasportare la misura, il
punto della circonferenza da cui vuoi partire e la
misura stessa.
Devi risolvere due problemi:
1. M non è stato definito come punto della
circonferenza: in queste condizioni non
potresti indicare M come punto di partenza per il trasporto
2. Per default, il trasporto di misura avviene in
senso antiorario
4. Rappresenta la cicloide come traccia, in modo da
seguire bene cosa succede.
LICEO SCIENTIFICO “VITTORIO VENETO” - MILANO
SCHEDA DI LAVORO n° 2 - La cicloide come luogo
Costruisci la cicloide con CABRI II, seguendo i primi tre
passi della scheda precedente
Ora puoi costruire la cicloide mediante lo strumento
LUOGO di Cabri.
Per rappresentare il luogo, occorre indicare
in sequenza il punto che appartiene al luogo
geometrico ed il punto che lo genera varian-
Hai individuato gli oggetti che ti occorrono?
Luogo geometrico
____________________________
Al variare di ________________________________
do in modo indipendente.
Per dare l’idea di una ruota che realmente rotola su una
linea potresti disegnare i suoi raggi.
Ti suggerisco i primi passaggi: traccia il diametro della
circonferenza di estremo P.
Traccia la normale al raggio.
Per continuare, usa lo strumento BISETTRICE
...........
Occorre individuare l’angolo mediante tre
punti nella sequenza: punto su una semiretta,
vertice dell’angolo, punto sull’altra semiretta.
Nascondi gli elementi superflui, utilizzati per la costruzione della ruota.
LICEO SCIENTIFICO “VITTORIO VENETO” - MILANO
SCHEDA DI LAVORO n° 3 - L’equazione della cicloide
Per individuare l’equazione della cicloide, fissa un
opportuno sistema di riferimento cartesiano.
Devi determinare le coordinate del punto P(x,y), in funzione del raggio r della circonferenza e dell’angolo φ, in
radianti.
Individua l’ascissa
OH = OC - HC = arco PC - HC = arco PC - QS
= ...........
Per l’arco PC, ricorda la definizione di radiante - Definiamo angolo radiante l’angolo il cui
arco PC rettificato ha la stessa lunghezza del
raggio della circonferenza.
Per trovare QS, lavora sul triangolo rettangolo PQS
Ricorda le relazioni tra archi associati
Individua l’ordinata
OK = HP = HQ + QP = ...............
Pertanto l’equazione della cicloide, in forma parametrica, è data da:
.......................................
LICEO SCIENTIFICO “VITTORIO VENETO” - MILANO
SCHEDA DI LAVORO n° 4 - Premessa
CURVATURA
Stai guidando su una strada in cui si alternano tratti rettilinei e tratti con curve. Ti trovi, in questo momento, su
un tratto rettilineo: diciamo che in questo punto del percorso la curvatura è nulla.
Ora stai affrontando una curva stretta; possiamo dire
che ti allontani rapidamente dalla traiettoria rettilinea,
cioè dalla tangente al percorso: In questo punto il percorso ha una grande curvatura.
Ecco infine una curva ampia; devi modificare la traiettoria rettilinea ma lo fai con una piccola rotazione dello
sterzo: in questo punto il percorso ha una piccola curvatura.
Abbiamo dato un'idea intuitiva di cosa si intenda, nel
piano euclideo, per curvatura di una linea in un dato
punto. Diamo ora significato matematico a questa
nozione intuitiva, ragionando sulle linee piane più semplici che conosci.
Per le rette non c'è curvatura in alcun punto, la curvatura è sempre nulla.
Considera alcune circonferenze, di raggio diverso, che
hanno tutte in comune un punto P. È facile capire che
se aumenta il raggio delle circonferenze la curvatura
diminuisce.
È allora abbastanza naturale definire la curvatura per
ciascuna circonferenza come l'inverso del suo raggio r
curvatura = 1/r
Questa definizione è indipendente dalla scelta del
punto P: per una data circonferenza la curvatura dipende solo dal raggio ed è uguale in tutti i punti.
Del resto se devi guidare un'automobile su un percorso
perfettamente circolare non dovresti, una volta trovata
la giusta rotazione dello sterzo, effettuare più alcuna
correzione.
Vediamo rapidamente come si possa definire la curvatura in un punto P per una generica linea curva g.
Cerchiamo di approssimare, nelle vicinanze di P, la
nostra linea con una circonferenza: in tal caso possiamo
dire che la curvatura di g in P è uguale alla curvatura di
questa circonferenza.
Le circonferenze sono linee piane a curvatura costante e la loro CURVATURA è uguale
all'inverso del raggio.
Si potrebbe dimostrare che le uniche linee
piane a curvatura costante sono le rette
(curvatura zero) e le circonferenze (curvatura 1/r).
LICEO SCIENTIFICO “VITTORIO VENETO” - MILANO
Per determinare la circonferenza che meglio approssima
g in P, considera due punti A e B su g molto vicini al punto
P. Sai che per tre punti non allineati passa una e una sola
circonferenza, quindi per A, P e B passa una ben determinata circonferenza. Se ora fai tendere verso P sia il punto
A che il punto B, individui una circonferenza limite che
prende il nome di cerchio osculatore a g in P.
Per RAGGIO DI CURVATURA e CENTRO DI
CURVATURA di una curva g in un punto P si
intende rispettivamente il raggio e il centro
del cerchio osculatore a g in P.
Naturalmente per una generica linea curva
piana la curvatura varierà al variare del
punto P.
EVOLUTA
INVILUPPO: è un modo di descrivere una
curva tramite una famiglia di curve.
Una prima caratterizzazione intuitiva dice
che una famiglia di curve inviluppa una
curva G se ogni elemento della famiglia è
tangente a G.
La famiglia di rette della figura seguente inviluppa una parabola, cioè ogni retta della
famiglia è tangente alla parabola.
La retta normale ad una curva in un suo
punto è la retta perpendicolare alla retta
tangente alla curva in quello stesso punto.
L'evoluta di una curva è l'inviluppo delle sue
rette normali.
Abbiamo visto che il cerchio è la sola curva piana con
curvatura costante, mentre nelle altre la curvatura varia
da punto a punto e, per misurarla, si cerca, tra tutti i cerchi che passano per quel punto, quello che approssima
meglio la curva: il cerchio osculatore.
I centri dei cerchi osculatori stanno su una seconda
curva, che si chiama evoluta della prima.
LICEO SCIENTIFICO “VITTORIO VENETO” - MILANO
SCHEDA DI LAVORO n°4 – L’EVOLUTA DELLA CICLOIDE
Si chiama evoluta di una curva il luogo geometrico dei suoi
centri di curvatura.
Considera prima una proprietà notevole della cicloide.
Traccia la retta tangente alla cicloide nel punto P e la retta
normale passante per P.
La normale alla cicloide in un suo
punto P passa sempre per il punto
di contatto C della circonferenza
generatrice con la direttrice.
Quindi, la tangente alla curva nel
punto P è la perpendicolare alla
normale n.
Le rette normali per ogni punto P della cicloide passano per i
suoi centri di curvatura. Costruendo l'inviluppo delle rette
normali alla cicloide si ottiene la sua evoluta.
Ora puoi costruire l'evoluta di una cicloide mediante lo
strumento di Cabri “luogo”.
Per la costruzione dell’evoluta
della cicloide puoi partire dalla
figura ottenuta con la precedente
costruzione.
Utilizza lo strumento “luogo” per
costruire la curva che si ottiene
come inviluppo delle rette normali
ai punti della cicloide al variare del
punto di contatto C.
L’evoluta di una cicloide è ancora una cicloide traslata di
metà base lungo la direttrice ed abbassata di una distanza pari
all'altezza della cicloide lungo la verticale.
Osserva: per costruzione, la
normale alla cicloide è tangente
alla sua evoluta.
LICEO SCIENTIFICO “VITTORIO VENETO” - MILANO
SCHEDA DI LAVORO n° 5 - Epicicloidi ed ipocicloidi
Obiettivo: costruire l’epicicloide con CABRI, utilizzando
lo strumento LUOGO di un punto C’, solidale alla circonferenza generatrice, al variare di un punto C su un segmento AB
Predisponi opportunamente CABRI:
dal menu OPZIONI/PREFERENZE seleziona la misura
degli angoli in radianti e porta a 500 il numero di
oggetti di un luogo.
CABRI misura solo angoli minori di un angolo piatto: pertanto il problema da risolvere è come far ruotare di 360°
un punto sulla circonferenza fissa dell’epicicloide.
Costruisci:
- un segmento AB=2R
- il suo punto medio O
- la circonferenza di centro O e raggio R
- un punto C appartenente al diametro
- la retta perpendicolare in C ad AB, che incontra la
circonferenza in P (e in Q)
Misura:
- il raggio OA
- l’angolo AOP, in radianti, nel verso antiorario
Calcola la lunghezza dell’arco AP di circonferenza
Costruisci ora la circonferenza direttrice, con centro in
un punto K e raggio uguale ad R.
Sia Z un suo punto; “trasporta” la lunghezza dell’arco AP,
a partire da Z e indica con E il punto: come puoi ben
vedere, muovendo C su AB, il punto E compie mezzo
giro sulla circonferenza direttrice.
Come pensi di poter superare questo problema?
Si definisce roulette una curva descritta da un
punto solidale con una curva, detta generatrice, la quale rotoli senza strisciare su un’altra
curva, detta direttrice.
La cicloide è un caso particolare di roulette,
per la quale la curva generatrice è una circonferenza e la direttrice è una retta.
Se la direttrice è una circonferenza e la curva
generatrice un’altra circonferenza di raggio
minore (r<R), che rotola all’esterno della circonferenza fissa, si ha l’epicicloide, mentre se
la circonferenza generatrice rotola all’interno, si ha l’ipocicloide.
LICEO SCIENTIFICO “VITTORIO VENETO” - MILANO
SCHEDA DI LAVORO n° 6 - L’epicicloide come luogo
Costruisci la circonferenza direttrice γ, con centro in un
punto K e raggio uguale ad R.
Sia Z un suo punto; “trasporta” la doppia lunghezza dell’arco AP, a partire da Z e indica con E il punto: come
puoi ben vedere ora, muovendo C su AB, il punto E
compie un giro completo sulla circonferenza direttrice.
Preso un punto S sul segmento OA, costruisci la circonferenza γ’ di raggio r=OS, che “rotola” sulla circonferenza
direttrice e tangente ad essa.
Analogamente a quanto fatto per la cicloide, ora devi
costruire il punto C’, luogo dell’epicicloide, come punto
che rotola su γ’ descrivendo un arco lungo quanto l’arco ZE.
Per costruire C’ utilizza ancora lo strumento “trasporto
di misura”.
Attenzione:
- il punto E deve essere definito come punto appartenente alla circonferenza g’.
- quale misura devi “trasportare”?
Se hai risolto correttamente i problemi precedenti, ora
sei in grado di costruire il luogo di C’ su γ’ al variare di C
sul segmento AB.
Al variare del raggio r=OS, si vede che non sempre l’epicicloide si chiude: riesci a stabilire sotto quali condizioni
l’epicicloide si chiude?
Nella scheda precedente abbiamo visto che
CABRI misura solo angoli minori di un angolo
piatto, ma il problema si può risolvere “trasportando” sulla circonferenza direttrice il
doppio della lunghezza dell’arco AP
Nascondi gli elementi della figura che non ti
interessano direttamente