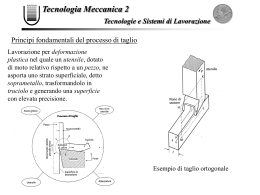
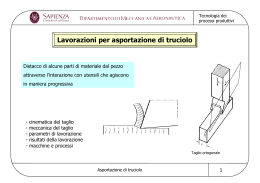
TEORIA DEL DENIS
La velocità di taglio Vt dipende:
 dalla durezza del materiale da lavorare;
 dal tipo di utensile (materiale, geometria,…);
 dal tipo di raffreddamento.
Il Denis considera la sezione del truciolo q=pa costante e traccia le
curve di produzione ponendo in ascissa la velocità di taglio Vt [m/min]
e in ordinata il volume del truciolo Q [cm3] asportato tra una “affilatura”
e l’altra.
Per la simulazione usare la barra spaziatrice, un click del mouse, i tasti freccia,
le parole calde (ovvero quelle sottolineate), i bottoni. Su alcune diapositive al
passaggio del mouse sui simboli si viene “mandati” alla loro definizione.
Quando l’animazione della diapositiva termina compare:
by ugo apostolo
Fine diapositiva
Le curve di produzione sono del tipo:
CONDIZIONI AL CONTORNO
Q = pa = cost
Q[cm3]
HVmateriale = cost
Qmax
UTENSILE = cost
4
Vt   Vt
3
Qe
e
Qmax
1
Qe   Qmax
2
0
Vtmin
VtQmax
Vte
Vtl
Vt[m/min]
by ugo apostolo
Fine diapositiva
Dove:
• Vtmin velocità di taglio minima; dettata dal numero di giri minimo della
macchina e dal minimo diametro lavorabile in tornitura cilindrica (sarà
nulla nelle operazioni di sfacciatura);
• VtQmax velocità di taglio dove la produzione di truciolo è massima
(Q=Qmax); essa è la velocità che offre la massima durata dell’utensile;
• Vtl velocità di taglio limite dove la produzione di truciolo è nulla (Q=0);
adottandola l’utensile appena accostato si ottunde (non “taglia” più);
• Vte velocità di taglio economica; realizza il miglior sfruttamento della
macchina. Si ha una produzione di truciolo QeQmax/2 ma il tempo per
ottenerla è minore.
4
Vt   Vt
3
e
Qmax
Per la dimostrazione di questa affermazione vedere la diapositiva successiva
nella quale viene confrontato il tempo per asportare un certo volume del
truciolo adottando le due sopramenzionate velocità di taglio
by ugo apostolo
Fine diapositiva
Q[cm3]
ttot
ttot
Q
Tcu
Qmax
m
Qe
h
0
T
t[min]
by ugo apostolo
T
Fine diapositiva
• T durata del tagliente, ovvero tempo durante il quale l’utensile
asporta truciolo
• Tcu tempo necessario per cambiare il tagliente
•
Q
volume del truciolo che si desidera asportare
• ttot tempo totale per asportare il volume del truciolo desiderato
• Qmax volume del truciolo asportato adottando la velocità VtQmax
• Qe volume di truciolo asportato adottando la velocità Vte
• tgm rappresenta la VtQmax
• tgh rappresenta la Vte
Cliccando su rappresenta si dimostrerà il legame tra le tangenti e le velocità di taglio
by ugo apostolo
Fine diapositiva
Dimostrazione
Poiché il volume del truciolo w [cm3/min] è dato dalla seguente espressione:
w  a  p  Vt
avremo che nella durata T[min] si asporterà il volume Q[cm3] dato da:
Q  a  p  Vt  T
Se ap=q=1 mm2=cost avremo:
Q  Vt  T
Dunque nel piano t,Q è l’equazione di una retta uscente dall’origine dove Vt
rappresenta il coefficiente angolare, cioè la tangente dell’angolo formato tra
l’asse delle ascisse e la retta stessa.
Ultima diapositiva
by ugo apostolo
Fine diapositiva