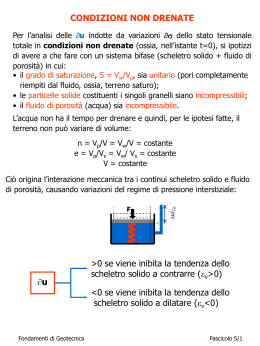
CONDIZIONI NON DRENATE
Per l’analisi delle u indotte da variazioni s dello stato tensionale
totale in condizioni non drenate (ossia, nell’istante t=0), si ipotizzi
di avere a che fare con un sistema bifase (scheletro solido + fluido di
porosità) in cui:
• il grado di saturazione, S = Vw/Vp, sia unitario (pori completamente
riempiti da liquido, ossia, terreno saturo);
• le particelle solide costituenti i singoli granelli siano incompressibili;
• il fluido di porosità (acqua) sia incompressibile.
L’acqua non ha il tempo per drenare e quindi, per le ipotesi fatte, il
terreno non può variare di volume:
n = Vp/V = Vw/V = costante
e = Vp/Vs = Vw/ Vs = costante
V = costante
F
u
Du/w
Ciò origina l’interazione meccanica tra i continui scheletro solido e fluido
di porosità, causando variazioni del regime di pressione interstiziale:
>0 se viene inibita la tendenza dello
scheletro solido a contrarre (v>0)
<0 se viene inibita la tendenza dello
scheletro solido a dilatare (v<0)
Geotecnica
Fascicolo 5/1
Per fissare le idee si immagini di portare in conto, pur se
minima, la compressibilità dell’acqua.
Come detto, l’applicazione di un incremento delle tensioni
totali s in condizioni non drenate produce delle u, e l’acqua,
pur se intrappolata nello scheletro solido, varia il proprio
volume secondo la relazione:
DVw 
n
Vp
V

Vw
n V
u 
u
Kw
Kw
Vw
per S  1 (essendo : Vp  Vw ).
V
D’altra parte, ipotizzando un comportamento elastico, lineare
ed isotropo dello scheletro solido, le s indotte in condizioni
non drenate (s=s-u) producono una variazione di volume
pari a:
V
DV  V   v  p
K
K 
E
3  (1  2  )
Ovviamente deve risultare:
V
n V
V
n V
p 
u 
(p  u) 
u
K
Kw
K
Kw
Ossia:
(4)
Geotecnica
u 
1
p  b  p
1  n  K K w
Fascicolo 5/2
Data la differenza di comportamento tra i terreni reali ed il mezzo
elastico, per tenere conto dell’accoppiamento volumetricodistorsionale delle terre...

...la (4) può scriversi:
u  b  (p  a  q)
Nel mezzo elastico:
b
1
;

1  n K Kw
a0
Inoltre, tenuto conto che Kw  K, si ottiene:
b
1
1

1  n K Kw
il che, verificato all’uguaglianza, equivale a reintrodurre l’ipotesi di
incompressibilità del fluido di porosità.
Geotecnica
Fascicolo 5/3
Relazione di Skempton
s1
Nelle prove geotecniche di laboratorio spesso
si incontrano condizioni di compressione in
s2=s3
simmetria radiale. In tali condizioni:
s3=s2
1
(s1  2  s3 )
3
q  (s1  s3 )
p 
Sostituendo nella (4) si ottiene:
u 

1
s1  2  s3  (s3  s3 )

1  n  K K w
3
1
1
[s3  (s1  s3 )]
1  n  K K w
3
Per tener conto del diverso comportamento meccanico dei terreni
rispetto al mezzo elastico, Skempton propone:
u  B  [s3  A  (s1  s3 )]
Nel mezzo elastico ed in condizioni di compressione triassiale:
B  b 1
A
1
3
NEI TERRENI REALI A  1/3
Geotecnica
Fascicolo 5/4
s3
In condizioni di estensione triassiale:
s2=s1
s1=s2
1
(s3  2  s1 )
3
q  (s1  s3 )
p 
Sostituendo nella (4) si ottiene:
u 

1
s3  2  s1  (2  s3  2  s3 )


1  n  K Kw
3
1
2
[s3  (s1  s3 )]
1  n  K K w
3
Pertanto, nel mezzo elastico ed in condizioni di estensione
triassiale:
B  b 1
A
2
3
NEI TERRENI REALI A  2/3
Geotecnica
Fascicolo 5/5
Geotecnica
Fascicolo 5/6