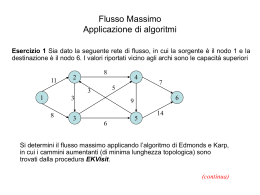
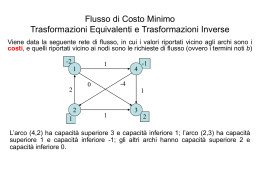
Flusso di Costo Minimo
Applicazione di algoritmi: cancellazione cicli negativi (CCN)
Premessa: si assume di aver risolto (correttamente!) un precedente esercizio sul
Flusso Massimo (con un qualunque algoritmo). Ci riferiamo a questo esercizio
come “Esercizio 1”. Il testo dell’esercizio 1 deve ovviamente specificare una rete
con le capacità superiori sugli archi.
Esercizio 1 Si consideri la seguente rete di flusso, in cui le capacità superiori sono
tutte pari a due, ad esclusione di quelle degli archi (s,2) e (3,t), che sono pari a 3,
come indicato in figura. Si determini un flusso di valore massimo da s a t…
1
4
s
t
3
2
3
3
Soluzione: il flusso di valore massimo, pari a v=5, è descritto nella seguente figura.
2
1
2
4
2
0
2
s
2
3
2
t
0
3
3
1
In realtà, a noi interessa soprattutto il grafo residuo relativo al flusso suddetto, cioè
il grafo residuo ottenuto all’ultima iterazione dell’algoritmo per il Flusso Massimo,
che è descritto nella seguente figura (sono mostrate le capacità residue).
2
2
s
1
4
2
2
2
2
t
1
3
2
1
1
3
3
Esercizio 2 (algoritmo CCN) Definiamo un problema di Flusso di Costo Minimo
(MCF) a partire dal problema di Flusso Massimo dell’esercizio 1, definendo costi
sugli archi come indicato in figura. Il nodo s ha una richiesta di flusso pari a -v, il
valore del flusso massimo dell’esercizio 1; il nodo t ha una richiesta di flusso pari a
v. Gli altri nodi sono di transito.
1
1
4
0
0
4
2
s
0
0
2
t
1
3
0
1
Mostrare che la soluzione ottima x’ del problema MCF si ottiene, a partire dal
flusso ottimo x dell’esercizio precedente, cancellando un solo ciclo di costo
negativo. Si chiede di:
1.calcolare il costo della soluzione x;
2.identificare il ciclo negativo, il suo costo e la sua capacità;
3.fornire il flusso ottimo x’ e il suo costo;
4.fornire un certificato di ottimalità per il flusso x’.
Non si richiede di applicare specifici algoritmi per la ricerca del ciclo, che può
essere facilmente identificato per ispezione.
Svolgimento
Possiamo, per cominciare, identificare la rete su cui è definito il problema MCF: a ciascun
arco si associa la coppia [costo,capacità superiore]; ai nodi s e t associamo le domande -5
e +5.
1
[0, 2]
[1, 2]
4
[0, 2]
[4, 2]
-5
s
t 5
[1, 2]
[2, 2]
[0, 2]
[0, 3]
2
[1, 2]
3
[0, 3]
NOTA: si tratta della “rete trasformata” su cui abbiamo applicato l’algoritmo SSP!
Nota: identificare il problema MCF è un passo utile, anche se non indispensabile per lo
svolgimento dell’esercizio, visto che in pratica lavoreremo soltanto sul grafo residuo.
Punto 1 costo della soluzione x.
Confrontando i flussi sugli archi relativi a x (dalla slide 2) e i costi assegnati agli
archi nel problema MCF, vediamo che gli unici archi che hanno sia il flusso che il
costo diversi da zero sono (1,4), (2,1) e (2,3)
1
1
0
4
0
4
costi
2
s
0
0
2
1
2
t
1
0
3
1
2
4
2
0
2
s
2
3
2
1
t
0
3
Dunque il costo di x è (1  2) + (2  2) + (1  1) = 7
3
flussi
Punto 2 identificazione del ciclo
Dobbiamo per prima cosa identificare il grafo residuo relativo al flusso ottimo x
dell’esercizio sul flusso massimo.
Per fare questo, riprendiamo il grafo residuo ottenuto alla fine dell’esercizio sul
flusso massimo (slide 2) e lo completiamo associando a ciascuno arco il costo
corrispondente, oltre alla capacità residua che già abbiamo.
Ovviamente, i costi sugli archi del grafo residuo sono ottenuti dai costi assegnati
dall’esercizio.
Grafo residuo con costi e capacità residue:
[costo,capacità]
[-1,2]
[0,2]
1
4
[0,2]
[0,2]
[4,2]
s
[-2,2]
[0,3]
2
t
[1,1]
[-1,1]
[1,1]
3
[0,3]
Sul grafo residuo identifichiamo il ciclo negativo (1,2,3,1).
Il costo è -2+1+0=-1.
La capacità è 1, determinata dall’arco (2,3).
[-1,2]
[0,2]
1
4
[0,2]
[0,2]
[4,2]
s
[-2,2]
[0,3]
2
t
[1,1]
[-1,1]
[1,1]
3
[0,3]
Punto 3 calcolo della soluzione ottima x’
Dobbiamo spedire un flusso 1 (pari alla capacità) lungo il ciclo negativo (1,2,3,1)
[-1,2]
[0,2]
1
4
[0,2]
[0,2]
[4,2]
s
[-2,2]
t
[1,1]
[0,3]
[-1,1]
2
[0,3]
3
[1,1]
Dopo la spedizione del flusso sul ciclo, il nuovo grafo residuo è il seguente
[-1,2]
[0,2]
1
[2,1]
s
4
[0,1]
[4,2]
[0,1]
[-2,1]
t
[1,1]
[0,3]
2
[0,2]
[-1,2]
3
[0,3]
Dal nuovo grafo residuo otteniamo (come visto per il problema di Flusso Massimo)
il flusso (ottimo) x’:
2
1
2
4
2
flussi
0
1
s
1
3
2
2
t
0
3
3
Il costo di x’ si ottiene come:
costo di x + (costo del ciclo  capacità del ciclo) = 7 + (-1  1) = 6
Nota: per verifica, si può calcolare il costo moltiplicando i nuovi flussi sugli archi
per i costi.
Nota: il flusso ottimo x’ è quello individuato, sulla rete trasformata, nell’esercizio di
applicazione dell’algoritmo SSP.
Punto 4 Ricerca di un certificato di ottimalità
Metodo “informale”: possiamo risolvere il problema sfruttando questa proprietà:
Se un arco (i,j) non è né vuoto né saturo, nel grafo residuo compaiono i due
archi (i,j) e (j,i), con costi c[i,j] e –c[i,j], rispettivamente; dunque, affinchè
entrambi gli archi abbiano costo ridotto non-negativo, occorre che questo
costo ridotto sia per entrambi zero; questo permette, dato il potenziale di uno
dei due nodi, di fissare univocamente l’altro.
Dunque, fissato arbitrariamente il potenziale di un nodo, possiamo derivare i
potenziali di altri nodi. Per i nodi il cui potenziale non viene fissato in questo modo
dobbiamo scegliere il potenziale in modo da rendere non-negativi i costi ridotti degli
archi adiacenti. Più in generale, per i nodi il cui potenziale non viene fissato,
possiamo determinare gli intervalli a cui tale potenziale deve appartenere.
2
[3,4]
-1
1
s
0
2
0
4
1
-2
2
0
4
-1
t
3
2
Trascuriamo per il momento i nodi s e t.
1. Diamo (arbitrariamente) al nodo 2 potenziale 0.
2. Diamo al nodo 1 potenziale 2 per avere costi ridotti nulli sugli archi (1,2) e (2,1),
corrispondenti ad un arco non vuoto e non saturo.
3. Diamo al nodo 3 potenziale 2 per avere costi ridotti nulli sugli archi (1,3) e (3,1),
corrispondenti ad un arco non vuoto e non saturo.
4. Il potenziale del nodo 4 non è fissato, ma deve essere:
• Almeno pari a 1, per rendere non-negativo il costo ridotto dell’arco (4,3);
• Almeno pari a 3, per rendere non-negativo il costo ridotto dell’arco (4,1);
• Non maggiore di 4, per non rendere negativo il costo ridotto dell’arco (2,4).
Dunque il potenziale del nodo 4 deve appartenere all’intervallo [3,4].
2
[3,4]
-1
1
0
≤0 s
0
2
0
0
0
4
t ≥p4
1
-2
2
0
4
-1
0
3
2
Consideriamo ora i nodi s e t:
• Il potenziale del nodo t deve essere almeno pari a quello del nodo 4, per rendere
non negativo il costo ridotto sull’arco (t,4); di conseguenza, il costo ridotto
dell’arco (t,3) risulterà positivo;
• Il potenziale del nodo s deve essere minore o uguale a zero, per rendere non
negativo il costo ridotto sull’arco (2,s); di conseguenza, il costo ridotto dell’arco
(1,s) risulterà positivo.
Tra i vettori di potenziali che rispettano i limiti visti possiamo scegliere, ad esempio:
π = [0,2,0,2,3,3] [s,1,2,3,4,t]
Questo vettore costituisce il certificato di ottimalità per x’ richiesto.
Nota: è lo stesso vettore di potenziali trovato applicando l’algoritmo SSP.
Metodo formale: si risolve un problema di cammino minimo con radici multiple, in
cui tutti i nodi sono radici. Questo è equivalente a risolvere il problema SPT di
radice r sul grafo riportato qui sotto, dove gli archi uscenti da r hanno costo zero.
r
-1
0
-1
1
4
0
-3 s
0
2
0
4
2
t
1
-2
0
-3
0
-1
0
0
3
-1
In questo caso, la soluzione trovata è unica, e corrisponde al vettore delle distanze minime
da r, riportate in blu nella figura. Il corrispondente albero dei cammini minimi è quello
evidenziato (notare che i nodi 4 e t sono “figli” della radice).