Flusso Massimo
Applicazione di algoritmi
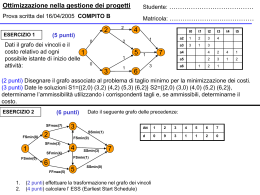
Esercizio 1 Sia dato la seguente rete di flusso, in cui la sorgente è il nodo 1 e la
destinazione è il nodo 6. I valori riportati vicino agli archi sono le capacità superiori
11
8
2
5
3
1
3
8
3
4
7
6
9
6
5
14
Si determini il flusso massimo applicando l’algoritmo di Edmonds e Karp,
in cui i cammini aumentanti (di minima lunghezza topologica) sono
trovati dalla procedura EKVisit.
(continua)
Ad ogni iterazione mostrare:
•il grafo residuo relativo al flusso corrente;
•l’albero determinato dalla procedura di visita del grafo residuo;
•il cammino aumentante determinato e la sua capacità;
•il nuovo valore del flusso.
Al termine dell’ultima iterazione, mostrare il flusso di valore massimo (cioè il
vettore x dei flussi sugli archi) e il taglio minimo ottenuti.
Nota: si assuma che, nel grafo residuo, gli archi in ciascuna forward star siano
visitati in ordine crescente di indice del nodo testa. L’ordine in cui sono visitati
gli archi nella backward star è ininfluente.
11
2
11
∞
4
3
8
7
5
3
1
Iterazione 1
8
8
6
9
3
7
1, 2, 3, 4, 5, 6
14
5
6
8
Evoluzione della fila
6
Cammino aumentante trovato: (1,2,4,6). Capacità: 7. Nuovo valore del flusso: 7
Nuovo grafo residuo
4
∞
7
1
1
2
5
3
3
8
3
4
7
7
6
9
6
5
14
4
2
4
∞
7
1
4
7
5
3
3
8
Iterazione 2
1
1
7
6
9
3
6
1, 2, 3, 4, 5, 6
14
5
6
8
Evoluzione della fila
6
Cammino aumentante trovato: (1,3,5,6). Capacità : 6. Nuovo valore del flusso: 13
Nuovo grafo residuo
4
∞
7
1
6
2
1
2
5
3
3
3
4
7
7
6
9
6
6
5
8
4
2
4
∞
7
1
4
7
5
3
3
6
2
7
6
9
3
6
Evoluzione della fila
1
1, 2, 3, 4, 5, 6
8
5
6
2
Iterazione 3
1
1
1
Cammino aumentante trovato: (1,2,4,5,6). Capacità: 1. Nuovo valore del flusso: 14
Nuovo grafo residuo
2
3
∞
8
1
6
2
4
8
5
3
3
3
7
1
8
6
6
7
5
7
3
2
3
∞
8
1
4
8
5
3
3
6
Iterazione 4
2
2
7
1
8
3
2
6
7
2
1, 2, 3, 4, 5, 6
7
5
6
Evoluzione della fila
2
Cammino aumentante trovato: (1,3,4,5,6). Capacità: 2. Nuovo valore del flusso: 16
Nuovo grafo residuo
2
3
∞
8
1
8
4
8
3
3
3
7
3
6
9
2
3
6
6
5
5
Iterazione 5
3
2
3
∞
8
1
8
4
8
3
3
3
7
3
6
9
2
3
6
6
Evoluzione della fila
1, 2, 3, 4, 5, 6
5
5
Cammino aumentante trovato: (1,2,3,4,5,6). Capacità: 3. Nuovo valore del flusso: 19
Nuovo grafo residuo
2
∞
11
1
8
4
8
7
3
3
6
3
12
5
3
6
6
5
2
Iterazione 6
2
∞
11
1
8
4
8
7
3
3
6
3
12
5
3
6
6
5
Evoluzione della fila
1
2
Non ci sono cammini aumentanti. Il valore del flusso massimo è 19
Il taglio minimo individuato è Ns= {1}, Nt = {2,3,4,5,6}
Ricostruzione del flusso x
2
11
1
4
8
7
3
3
8
6
3
12
5
3
6
2
5
6
Il valore del flusso su ciascun arco corrisponde alla capacità degli archi “inversi”
(quelli rossi); riportiamo i valori sul grafo originale
11 11
2
3 3
1
8 8
8 8
3
0 3
4
5 5
7 7
6
6 9
6 6
5
14 12