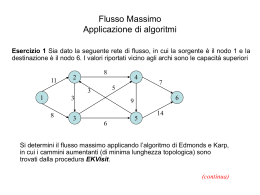
Riconoscimento di Grafi Bipartiti
Certificati di (non) bipartizionabilità
•Il grafo è orientato ma si considera come non orientato
•Per brevità svolgiamo in parallelo due casi:
– Senza archi rossi: il grafo è bipartito
– Con gli archi rossi: il grafo non è bipartito
• Tipologia di esercizio per il caso bipartito
– (1) Fornire un certificato di bipartizionabilità, mostrando l’albero alternante
determinato dalla procedura Bipartito;
• Tipologie di esercizio per il caso non bipartito
– (2) Fornire il certificato di non bipartizionabilità determinato dalla procedura
Bipartito; mostrare l’albero alternante determinato fino al momento in cui la
procedura termina, evidenziando nella figura il certificato trovato;
– (3) Fornire l’insieme di archi da eliminare (per ottenere un grafo bipartito)
determinato dalla procedura Bipartito; mostrare l’albero alternante
determinato.
Attenzione: non è detto che gli archi da eliminare siano quelli rossi!
Specifiche per la procedura Bipartito
• Il nodo scelto come radice è il nodo 1;
• L’insieme di nodi candidati è gestito come fila;
• Per ciascun nodo esaminato, la forward star è esaminata prima
della backward star;
– Gli archi in ciascuna forward star sono esaminati in ordine crescente di
indice del nodo testa;
– Gli archi in ciascuna backward star sono esaminati in ordine crescente
di indice del nodo coda;
– Oppure: l’ordine in cui gli archi in ciascuna backward star sono
esaminati è ininfluente.
Attenzione: il risultato dell’esercizio comprende solo ciò che è esplicitamente
richiesto, non i passaggi intermedi!
1
2
3
1
4
2
5
6
7
8
9
10
11
12
1, 2, 5
Iterazione 1: estrazione ed elaborazione del nodo 1
5
1
2
3
1
4
2
5
6
7
8
9
10
11
12
1, 2, 5, 3, 6
Iterazione 2: estrazione ed elaborazione del nodo 2
3
5
6
1
2
3
1
4
2
5
6
7
8
9
10
11
12
1, 2, 5, 3, 6, 9
Iterazione 3: estrazione ed elaborazione del nodo 5
3
5
6
9
1
2
3
1
4
2
5
5
6
7
8
3
6
9
10
11
12
4
7
1, 2, 5, 3, 6, 9, 4, 7
Iterazione 4: estrazione ed elaborazione del nodo 3
9
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
5
9
6
7
10
1, 2, 5, 3, 6, 9, 4, 7, 10
Iterazione 5: estrazione ed elaborazione del nodo 6
Iterazione 6: il nodo 9 viene estratto senza raggiungere alcun nodo, né modificare l’albero
Tipologia (1) (senza archi rossi):
normale iterazione
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
1, 2, 5, 3, 6, 9, 4, 7, 10, 8
8
Iterazione 7: estrazione ed elaborazione del nodo 4
5
9
6
7
10
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
5
9
6
7
10
1, 2, 5, 3, 6, 9, 4, 7, 10, 8, 11
8
11
Iterazione 8: estrazione ed elaborazione del nodo 7
Iterazione 9: il nodo 10 viene estratto senza raggiungere alcun nodo, né modificare
l’albero
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
5
9
6
7
10
1, 2, 5, 3, 6, 9, 4, 7, 10, 8, 11, 12
8
Iterazione 10: estrazione ed elaborazione del nodo 8
11
12
Iterazioni 11 e 12: i nodi 11 e 12 vengono estratti ed elaborati senza raggiungere alcun
nodo, né modificare l’albero
Risultati per la tipologia 1
•l’albero finale ottenuto
•la partizione dei nodi in due insiemi: {1,3,6,9,8,11} e {2,4,5,7,10,12}
Possibile variante:
•Si richiede solo il certificato, e cioè la partizione, non l’albero
Tipologia (2) (con archi rossi):
si rileva un conflitto,
si determina il certificato
e si termina
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
1, 2, 5, 3, 6, 9, 4, 7, 10, 8
8
Iterazione 7: estrazione ed elaborazione del nodo 4
Si rileva un conflitto con il nodo 10
Si determina il ciclo dispari (2,3,4,10,6,2)
5
9
6
7
10
Risultati per la tipologia 2
•l’ultimo albero determinato, e disegnato su di esso, il ciclo dispari
•è comunque opportuno indicare anche il ciclo, cioè la sequenza nodi
(2,3,4,10,6,2)
Possibile variante:
•Si richiede solo un certificato, e non l’albero: in questo caso basta fornire un
qualunque ciclo di lunghezza dispari, senza preoccuparsi del fatto che possa
essere identificato dalla procedura Bipartito; ad esempio, basterebbe fornire il
ciclo (7,11,12)
Tipologia (3) (con archi rossi):
si rileva un conflitto,
si marca un arco come
“da cancellare”
e si prosegue
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
5
9
6
7
1, 2, 5, 3, 6, 9, 4, 7, 10, 8
8
Iterazione 7: estrazione ed elaborazione del nodo 4
L’arco (4,10) crea un conflitto (ciclo dispari) e deve essere eliminato.
10
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
5
9
6
7
10
1, 2, 5, 3, 6, 9, 4, 7, 10, 8, 12, 11
8
Iterazione 8: estrazione ed elaborazione del nodo 7
11
12
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
5
9
6
7
10
1, 2, 5, 3, 6, 9, 4, 7, 10, 8, 12, 11
8
11
12
Iterazione 9: estrazione ed elaborazione del nodo 10, l’albero non si modifica
Iterazione 10: estrazione ed elaborazione nodo 8, l’arco (8,12) forma un ciclo
dispari e deve essere cancellato.
1
2
3
1
4
2
5
6
7
8
3
9
10
11
12
4
5
9
6
7
10
1, 2, 5, 3, 6, 9, 4, 7, 10, 8, 12, 11
8
11
12
Iterazione 11: estrazione ed elaborazione nodo 12, l’arco (12,11) forma un ciclo
dispari e deve essere cancellato.
L’ultima iterazione (nodo 11) non modifica l’albero.
Risultati per la tipologia 3
•l’albero finale determinato
•l’insieme di archi eliminati: (4,10), (8,12), (11,12)
•è opportuno fornire esplicitamente la bipartizione determinata per il grafo
rimanente, nel nostro caso {1,3,6,8,9,11,12} e {2,4,5, 7,10}
Possibile variante:
•Si richiede solo un insieme di archi da eliminare, e non l’albero: in questo
caso basta fornire
– un qualunque insieme di archi la cui eliminazione rende il grafo bipartito;
– una bipartizione per il grafo rimanente.
Ad esempio, avremmo potuto fornire l’insieme di archi rossi (4,10) e (7,12), e
quindi la stessa bipartizione trovata per la tipologia 1, cioè {1,3,6,9,8,11} e
{2,4,5,7,10,12}