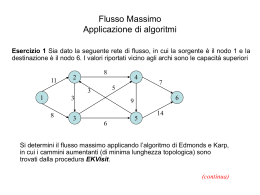
Flusso di Costo Minimo
Applicazione di algoritmi: Cammini Minimi Successivi (SSP)
Esercizio 1 Sia data la seguente rete di flusso, in cui i valori riportati vicino agli
archi sono i costi, e quelli riportati vicino ai nodi sono le richieste di flusso
(ovvero i termini noti b)
-2
1
1
1
2
1
-1
-4
0
2
4
1
3
2
L’arco (4,2) ha capacità superiore 3 e capacità inferiore 1; l’arco (2,3) ha capacità
superiore 1 e capacità inferiore -1; gli altri archi hanno capacità superiore 2 e
capacità inferiore 0.
Passo 1. Si trasformi la rete data in una rete equivalente con costi non negativi,
capacità inferiori nulle, singola origine e singola destinazione. Si determini la
costante F aggiunta alla funzione obiettivo nel corso della trasformazione.
Passo 2. Sulla rete trasformata si risolva il problema applicando l’algoritmo SSP
(cammini minimi successivi) che usa potenziali e costi ridotti. Ad ogni iterazione si
mostri:
•Valore e costo del flusso fino ad ora spedito dalla sorgente alla destinazione
•Il grafo residuo pesato relativo al flusso corrente (riportando i costi ridotti e le
capacità residue)
•L’albero dei cammini minimi sul grafo residuo, specificando le etichette ottime (si
intende le etichette di distanza d: non occorre riportare le etichette di capacità l)
•Capacità e costo (rispetto ai costi ridotti!) del cammino aumentante trovato
•Il nuovo vettore dei potenziali.
Non si richiede di utilizzare un algoritmo specifico per i cammini minimi, che
possono essere facilmente trovati per ispezione.
Passo 3. A partire dal flusso ottimo xT sulla rete trasformata si ottenga il flusso
ottimo x sulla rete originale. Si verifichi la relazione che lega il costo di xT, il costo
di x, e la costante F calcolata al Passo 1.
NOTE (1)
1. Il potenziale del nodo sorgente è sempre zero.
2. Dati i potenziali π, indichiamo i corrispondenti costi ridotti come c(π); sia d il
corrispondente vettore delle distanze ottime rispetto ai costi c(π). I nuovi
potenziali π’ sono ottenuti ponendo π’ := π + d . Allora, i nuovi costi ridotti c(π’)
possono ottenuti in due maniere equivalenti:
• Dai costi originali, usando i nuovi potenziali π’;
• Dai costi c(π), usando le etichette d: per ogni arco (i,j)
cij(π’) = cij(π) + di - dj
In pratica, è più facile utilizzare il secondo metodo, cioè ricavare i nuovi costi ridotti
utilizzando i costi ridotti attuali e le etichette d; questo permette infatti di lavorare
sempre sul grafo residuo dell’ultima iterazione, che è pesato rispetto ai costi ridotti
attuali.
Nel seguito utilizzeremo questo metodo; quando possibile (dopo la seconda iterazione)
mostreremo anche l’applicazione del primo metodo - ovviamente, i due metodi danno gli
stessi risultati, il primo metodo è mostrato solo come una maniera per controllare i
risultati durante lo svolgimento dell’esercizio.
NOTE (2)
L’esercizio richiede di fornire, ad ogni iterazione, il costo del flusso fino ad ora
spedito da s a t. Dunque, ad ogni iterazione, dobbiamo sommare al costo precedente
il costo del flusso spedito sul cammino aumentante utilizzato; questo costo è dato,
ovviamente, dal prodotto costo del cammino  unità di flusso spedite.
Il problema è che qui il “costo del cammino” si riferisce al costo originale, mentre
nel nostro algoritmo noi utilizziamo i costi ridotti, e dunque le lunghezze che
calcoliamo (le nostre etichette d) si riferiscono ai costi ridotti. Fortunatamente,
vale la seguente proprietà:
Sia d il vettore delle distanze ottime rispetto ai costi ridotti c(π); il costo
“vero” (cioè rispetto ai costi originali) del cammino aumentante è dato da
π’t = πt + dt
Quindi, sfruttando questa proprietà, possiamo calcolare il costo del flusso ad ogni
iterazione, utilizzando come costo “vero” del cammino usato il nuovo potenziale del
nodo destinazione.
Ovviamente, per fare questo dovremo ricordarci di aggiornare i potenziali prima di
calcolare il costo del cammino!
NOTE (3)
L’esercizio richiede di fornire, ad ogni iterazione, il nuovo grafo residuo con
capacità e costi ridotti. Per semplificare le operazioni, possiamo distinguere il
lavoro da svolgere sugli archi del cammino aumentante dal lavoro da svolgere
sui rimanenti archi:
• per gli archi del cammino aumentante, su cui spediamo flusso, dobbiamo
preoccuparci di determinare le nuove capacità residue, facendo attenzione agli
archi (“rossi” e/o “neri”) che compaiono o scompaiono dal grafo residuo; per
questi archi però non abbiamo bisogno di calcolare i nuovi costi ridotti, perché
(come sappiamo dalla teoria) i nuovi costi ridotti saranno uguali a zero; in
particolare, questo vale per ciascun arco (i,j) (“nero” o “rosso”) che fa parte del
cammino, e anche per l’eventuale arco “inverso” (j,i) (rispettivamente “rosso” o
“nero”) corrispondente a (i,j);
• per gli archi che non stanno nel cammino aumentante, su cui non spediamo
flusso, dobbiamo preoccuparci invece solo di determinare i nuovi costi ridotti,
perché le capacità residue non cambiano. Sappiamo dalla teoria che i nuovi costi
ridotti devono essere non-negativi, quindi la “comparsa” di un costo ridotto
negativo è segnale inequivocabile di un errore…
Ovviamente,
Passo 1 passaggio alla rete trasformata
Rete trasformata: a ciascun arco si associa la coppia [costo,capacità superiore]
1
[0, 2]
[1, 2]
4
[0, 2]
[4, 2]
-5
s
t 5
[1, 2]
[2, 2]
[0, 2]
[0, 3]
2
[1, 2]
3
[0, 3]
F = -13
(vedi esercizio sulle trasformazioni sintattiche)
Passo 2 esecuzione dell’algoritmo SSP
Iterazione 1 Flusso attuale: valore 0, costo 0. Potenziali: π=[0,0,0,0,0,0] [s,1,2,3,4,t]
0
[0, 2]
0
-5
1
[1, 2]
1
4
[0, 2]
[4, 2]
s
t 5
[1, 2]
[0, 2]
0
[0, 2]
[0, 3]
0
2
[0, 3]
3
[1, 2]
0
Cammino aumentante (s,1,3,t): costo 0; capacità 2. Etichette: d = [0,0,0,0,1,0] = π.
Valore del flusso 2, costo 20=0.
Nuovo grafo residuo pesato (costi ridotti e capacità).
1
[0, 2]
[0, 2]
4
[1, 2]
[3, 2]
-5
s
[2, 2] [0, 2]
[2, 2]
[0, 2]
[0, 3]
2
[1, 2]
3
[0, 1]
t 5
Passo 2 esecuzione dell’algoritmo SSP
Iterazione 2 Flusso attuale: valore 2, costo 0. Potenziali: π=[0,0,0,0,1,0] [s,1,2,3,4,t]
[0, 2]
1
1
1
4
[0, 2]
[1, 2]
[3, 2]
-5
s
t 5
[2, 2]
[2, 2]
[0, 2]
1
[0, 2]
[0, 3]
[0, 1]
2
3
[1, 2]
0
1
Etichette: d = [0,1,0,1,1,1]. Nuovo π=[0,0,0,0,1,0] + [0,1,0,1,1,1] =[0,1,0,1,2,1]; cammino
aumentante (s,2,3,t): costo 1; capacità 1. Nuovo valore del flusso 3; costo 0+11=1.
Nuovo grafo residuo pesato (costi ridotti e capacità).
[1, 2]
1
[0, 2]
4
[1, 2]
[2, 2]
-5
s
[2, 2]
[0, 1] [1, 2]
[0, 2]
[0, 2]
2
[0, 1]
[0, 1]
3
[0, 3]
t 5
Passo 2 esecuzione dell’algoritmo SSP
Iterazione 3 Flusso attuale: valore 3, costo 1. Potenziali: π =[0,1,0,1,2,1]. [s,1,2,3,4,t]
[0, 2]
0
1 0
1
4
[1, 2]
[1, 2]
[2, 2]
-5
s
t 5
[2, 2]
[0, 1] [1, 2]
[0, 3]
[0, 2]
1
[0, 2]
[0, 1]
2
3
0
0
[0, 1]
Cammino aumentante (s,2,3,1,4,t): costo originale 1+1=2; capacità 1. Etichette:
d = [0,0,0,0,0,1] . Nuovo π =[0,1,0,1,2,1] + [0,0,0,0,0,1] =[0,1,0,1,2,2].
Valore del flusso 4, costo 1+21=3.
[0, 1]
1
1
4
[1, 2]
[0, 1]
[0, 1]
[2, 2]
[0, 1]
-5
[1, 2] [0, 1]
s
t 5
[0, 1] [2, 2]
[0, 2]
[0, 1]
2
[0, 2]
[1, 3]
3
Passo 2 esecuzione dell’algoritmo SSP
Iterazione 4 Flusso attuale: valore 4, costo 3. Potenziali: π =[0,1,0,1,2,2]. [s,1,2,3,4,t]
1
[1, 2]
-5
s
[0, 1]
1
[1, 2]
[0, 1]
[0, 1]
[0, 2]
[0, 1]
0
2
[0, 2]
4
[2, 2]
1 1
[0, 1]
5
[0, 1]
t
[0, 1] [2, 2]
[1, 3]
3
1
1
Cammino aumentante (s,2, 1,4,t): costo originale 2+1=3; capacità 1. Etichette:
d = [0,1,0,1,1,1] . Nuovo π =[0,1,0,1,2,2] + [0,1,0,1,1,1] =[0,2,0,2,3,3].
Valore del flusso 5, costo 3+31=6. Flusso ottimo.
Grafo residuo finale:
[0, 2]
1
1
4
[0, 2]
[2, 2]
[1, 2]
5
[0, 1]
-5
s
t
[0, 1] [2, 2]
[0, 1]
[0, 3]
[0, 1]
[1, 3]
2
3
[1, 2]
Passo 3 Soluzione ottima sulla rete originale
(vedi esercizio sulle trasformazioni sintattiche)
-2
2
1
3
1
1
-1
4
0
2
1
1
3
2
I numeri vicini ai nodi sono i bilanci (flusso entrante meno flusso uscente); si può
verificare che corrispondono alle richieste.
Il costo totale del flusso è (costo × flusso)
2 × 1 + 1 × 1 + (– 4) × 3 + 0 × 1 + 1 × 2 = -7
(2,1)
(2,3)
(4,2)
(1,3)
(1,4)
Il costo del flusso ottimo sulla rete originale è dato dal costo sulla rete trasformata (6)
più la costante F (– 13).