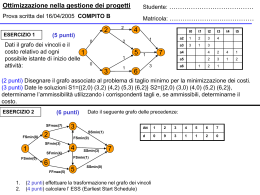
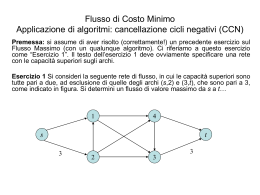
2. Grafi
Indice
Tipi di grafi
Rappresentazione di grafi
Misure su grafi
distanza minima
centralità dei nodi
betweenness, clustering
closeness,
Distribuzione dei gradi dei nodi
Esercizi:
Pajek
Octave:
Un grafo è un insieme di nodi (o vertici) V, collegati tra loro
da un insieme di archi [arcs,links] o spigoli (o collegamenti
o archi non orientati) [edges] E. Si indica con G=(V,E).
numero spigoli=|E|=m; numero vertici=|V|=n
L’ordine di un grafo è il numero di vertici n
Un grafo si dice semplice se non ha multiarchi (multiple arcs)
o loop
multiarco
loop
Nodi: persone, eventi, jobs, etc.
Archi: realazioni personali,
sequenze temporali, …
Un percorso (walk) è una sequenza di nodi adiacenti.
Un percorso chiuso è un percorso in cui il primo e l’ultimo vertice
coincidono ovvero che congiunge un nodo a se stesso
Due archi si dicono connessi se hanno un nodo in comune
Un cammino (path) è una sequenza di archi connessi
che congiunge due nodi (in modo tale che nessun nodo si ripeta)
Un ciclo è un cammino che congiunge un nodo a se stesso
Un grafo si dice connesso se dati due nodi qualsiasi esiste un
cammino che li congiunge
n1
n5
n2
n4
n3
Percorso diretto (Directed walk)
n5-n1-n2-n3-n4-n2-n3
Cammino diretto (Directed Path)
n5 n4 n2 n3
Cammino non diretto (Semipath)
n1 n2 n5 n4 n3
Ciclo (Cycle)
n2 n3 n4 n2
Ciclo non diretto (Semicycle) n1 n2 n5 n1
Un sottografo (sub-graph) di un grafo è un
grafo i cui nodi e archi sono un sottoinsieme
di quelli di G.
Una componente di un grafo è un sottografo connesso.
Grafo pesato
Un grafo è orientato (directed
graph o digraph) quando tutti i
suoi archi lo sono.
Un albero è un grafo connesso senza cicli
Un albero è un grafo tale che |n-m|=1
La struttura ad albero di un grafo permette di raggiungere tutti i nodi
con il minimo numero di archi 
Albero di Ricoprimento Minimo =minimum spanning tree (mst)
Un insieme di alberi disgiunti è una foresta
Algoritmi per calcolare il mst
Prim’s algorithm
Kruskal’s algorithm
Boruvka’s algorithm
Un grafo si dice completo se da ogni nodo si raggiunge qualsiasi altro
percorrendo un solo spigolo
Il numero di spigoli in un grafo completo è: m=n(n-1)/2
Il grado di ogni vertice è n-1
Un grafo si dice regolare se tutti i nodi hanno lo stesso grado
Come si rappresenta matematicamente un grafo
Matrice di adiacenza
Matrice binaria. E’ simmetrica se il grafo non è orientato e viceversa
n
n
j 1
j 1
ki   Aij   A ji ;
n7
1
4
2
3
E1 E2 E3
v1 v2 v3 v4
0
0
A
0

1
0 0 1
0 0 1
0 0 1

1 1 0
1

0
Inc  
0

1
v1
v2
v3
v4
Matrice adiacenza
0
1
0
1
0

0
1

1
v1
v2
v3
v4
Matrice Incidenza
141
241
341
411
421
431
Lista adiacenza
Se il grafo è pesato allora è descritto da una matrice W del tipo:
Matrice laplaciana:
L=Deg-A:
Esempio
Alcune proprietà:
Siano
g autovalori di L
L è sempre semidefinita positiva
Il numero degli autovalori nulli è quello delle componenti connesse
Distanza e diametro
La lunghezza di un cammino è il numero
di spigoli (link) in esso contenuti (per i
relativi pesi)
La distanza d(i,j) tra due nodi (non
necessariamente distinti) i e j è la lunghezza del
cammino minimo che li congiunge.
Il diametro di un grafo è la massima delle
distanze minime tra le coppie dei suoi vertici
Il diametro di un grafo completo è 1,
indipendente da n
La lunghezza caratteristica [characteristic
path length ], è la media delle distanze
minime
n(n-1)/2 =n° totale di link se la rete è non diretta
2m
2*8=16
Eigenvector centrality: Authorities and Hubs
Nelle reti orientate i gradi in entrata (xi) ed in uscita (yi) dei nodi
hanno un significato diverso.
Si deve risolvere un problema agli autovalori (anzi 2) Av=lv
WWW
Le authority (grande xi) contengono grandi informazioni su un
dato tema.
Gli hub (grande yi) dicono dove trovare quelle informazioni
Manuale Pajek
Eingenvector centrality
Un nodo è importante se ha «amici» importanti
La matrice di adiacenza A è non negativa (ha autovalori ≥0)
Il teorema di Perron-Froboenius afferma che se la rete è connessa
allora il massimo autovalore è reale e le componenti dell’autovettore
corrispondente sono positive
Le si può normalizzare e trovare un ranking dei nodi . La componente
con il valore più grande è quella con gli «amici più importanti».
E’ il metodo usato da Google. Una pagina è importante se puntata da
pagine importanti
Degree centrality e Degree centralization
Le persone sono centrali se l’informazione può facilmente raggiungerle
La degree centrality è Il più semplice indicatore di centralità di un nodo ovvero è
il numero dei sui vicini (il suo grado)
La degree centralization di una rete è la misura di quanto la sua struttura sia
lontana da quella di una rete a stella.
Esempio
v2
v1
v1
v3
v2
v5
v1
v3
v4
| V|
v5
v3
v5
A
C D (G ) 
v2
 deg(v * - deg(v ))
B
v4
C
i
i 1
(n - 2)(n - 1)
CD ( B) 
(2  1)  (2  2)  (2  2)  (2  1)  (2  2) 1
  0.17
12
6
C D ( A) 
v4
4  (4  1)  1 (4  4) 12

1
12
12
C D (C )  0
In una rete con linee multiple o loops (non semplice) il grado di un vertice è
diverso dal numero di vicini (e la centralization può essere >1). In questo caso
non è opportuno usare la misura di degree centralization
Closeness Centrality and Closeness Centralization
In una rete di comunicazione l’informazione raggiunge una persona più
facilmente ed in modo più corretto se il percorso che deve fare è breve.
La Closeness Centrality di un vertice è l’inverso della somma delle distanze del
vertice dagli altri divisa per il numero di vertici :
(Sum distanze dai vertici/ n°dei vertici) -1 = ( n°di vertici/sum distanze dai
vertici)
La Closeness Centralization è la variazione della closeness centrality dei vertici
divisa per la variazione della closeness centrality in una rete a stella delle stesse
dimensioni
N.B. Per calcolare le distanze i nodi devono essere connessi. La closeness
centralization è una misura definita solo su una componente connessa.
Centrality: efficiency (di un grafo)
Questa quantità è basata sull’assunzione che l’efficienza nella
comunicazione tra due nodi i e j è uguale a
L’efficienza del grafo G è definita così:
Il grado può non riuscire a cogliere l’importanza di un nodo
La betweenness (‘’essere tra’’) di un nodo i è il numero di cammini
minimi (geodesic paths) tra altri vertici che lo attraversano diviso per il
numero totale di cammini minimi .
Betweenneess Centrality and Betweenness Centralization
Una misura di centralità è quella dell’ «essere intermediario» ad esempio in una
rete di comunicazione cioè il flusso di informazioni che una persona può controllare
perché la attraversa.
La Betweenness centrality di un vertice è il numero di cammini minimi
(geodesiche) che attraversano un nodo diviso per il numero totale di cammini
minimi
La Betweenness centralization è la variazione della Betweenness Centrality dei
vertici divisa per la variazione della betweenness centrality in una rete a stella delle
stesse dimensioni.
La betweennees può essere una misura
della vulnerabilità del grafo ad attacchi
selettivi ai suoi nodi
degree
Alaska
Clustering coefficient
Il coefficiente di clustering Ci del nodo i è il numero di spigoli esistenti tra i suoi
nodi vicini diviso per tutti i nodi possibili tra i vicini stessi
21=7*6/2
In Pajek
CC1(v) 
2 E (G1 (v)
deg( v)(deg( v)  1)
Clustering coefficient
Deg(v)=degree of v
|E(G1(v)|=n°di connessioni tra i vicini di v
CC1 (v) 
2 E (G1 (v))
deg(v)(deg(v)  1)
deg(v)
CC (v) 
CC1 (v)
Max deg
'
1
0  CC '1 (v)  1
Il Clustering Coefficient del grafo è la media dei clustering dei nodi:
Esistono altre definizioni di clustering Coefficient che danno valori simili
(ma non identici)
Gli alberi hanno coefficiente di Clustering =0
Il Clustering misura la connessione dell’intorno di una rete e fornisce
un’altra misura della robustezza del grafo. Se un grafo ha un valore
di Clustering alto anche se eliminiamo un nodo il grafo rimane
connesso
Piccardi ACN2010
Esercizi:
Pajek
Applicazione delle misure di
centralità viste
Octave: degree distribution