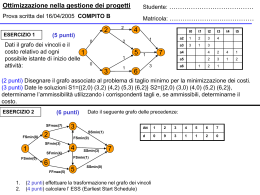
Presentazione di
Bruno Jannamorelli
Konigsberg …
Il problema dei 7 ponti di
Konigsberg
Partendo da una delle quattro zone della città,
esiste un percorso che permetta di ritornarvi
attraversando i sette ponti una e una sola volta?
Soluzione di EULERO:
Per ogni arco che
arriva su un vertice,
deve esserci un altro
arco che permette di
uscire da quel vertice.
Non esiste un percorso euleriano!
Konigsberg diventa Kaliningrad
… i ponti diventano nove!
Esiste un percorso euleriano?
Ecco un grafo che risolve il problema:
Non esiste un
percorso euleriano,
ma si può partire
da C e fermarsi in
D (o viceversa)
attraversando una e
una sola volta i 9
ponti.
Conclusione:
• Se un grafo connesso non ha vertici dispari, allora
può essere attraversato da un percorso ciclico
(euleriano), partendo da un vertice qualunque e
ritornando nello stesso vertice.
• Se un grafo connesso ha solo due vertici dispari A e
B, esiste un percorso che lo attraversa partendo da A
e fermandosi in B, o viceversa.
• Se un grafo connesso ha più di due vertici dispari,
non può essere attraversato da un solo percorso.
È possibile entrare in questa casa
attraversando le porte una e una sola volta?
Ecco un grafo che risolve il problema:
Ci sono quattro
vertici di
ordine dispari
…
Il percorso non esiste!
Avvio alla geometria premetrica
• attività topologiche
• attività che non richiedono l’uso di vere
e proprie metriche
Obiettivi:
• capacità di situare se stessi, gli altri e gli
oggetti in determinati spazi.
• capacità di effettuare percorsi
• capacità di leggere/produrre disegni
schematici per rappresentare situazioni
topologiche
• passaggio dalla tridimensionalità alla
bidimensionalità e viceversa.
“La topologia è la geometria …
del foglio di gomma”
.A
B
X
.A’
C
B’
X’
C’
Proprietà topologiche:
Sono quelle proprietà che restano
invariate rispetto alle trasformazioni
bicontinue e biunivoche
(omeomorfismi).
Omeomorfismo:
Corrispondenza tra i punti di una figura F e i
punti di una figura F’ tale che:
• La corrispondenza sia biunivoca:
ad ogni punto di F corrisponde uno e un sol
punto di F’, e viceversa.
• La corrispondenza sia continua nei due versi:
a punti “vicini” di F corrispondono punti
“vicini” di F’, e viceversa.
Esempi di omeomorfismi:
• deformazioni del foglio di gomma senza sovrapposizioni
o lacerazioni
(con le sovrapposizioni viene a mancare la
biunivocità, con le lacerazioni salta la continuità)
• Tagli-deformazioni-saldature.