Teoria dei linguaggi volgari
Anteprima sull’uso di linguaggi per rappresentare strutture di dati
Mauro Torelli
Note per il corso di Algoritmi e strutture di dati
1
Linguaggi
Un linguaggio è semplicemente un insieme di parole costruite su un determinato alfabeto di simboli
(numerici, caratteri o altro). Le presenti note scherzano sull’assonanza tra “teoria dei linguaggi formali” e
“teoria dei linguaggi volgari”, ma di fatto intendono presentare in modo leggero e (spero) divertente e facile
da ricordare classi di linguaggi formali particolarmente utili per introdurre strutture di dati e problematiche
rilevanti in informatica.
L’idea ispiratrice è quella di considerare alcune parole come “tabù” o “parolacce” e vedere che cosa si
può ricavare da questa idea. In realtà i linguaggi formali prescindono completamente dall’attribuire un
significato alle parole, mentre noi attribuiamo addirittura una connotazione etica o estetica a certe parole
“brutte”, ma solo per scherzo!
Vediamo subito un esempio. Se avete amici stranieri avrete probabilmente notato che hanno spesso
difficoltà a scrivere le parole italiane contenenti consonanti doppie (ieri vedevo un cartello “Si afita…”).
Potremmo allora aiutarli abolendo le doppie: ss, tt, pp, gg, ecc. sono tutte tabù (anzi, tute). OK, forse non è
una buona idea: non vogliamo aplicare (!) la nostra teoria ai linguagi naturali, ma solo a linguagi artificiali
(formali) interesanti.
Per (un altro) esempio può essere interessante considerare linguaggi in cui l’ordine dei simboli non è
rilevante: travaglio e giravolta diventano la stessa parola, come pure (è importante per la nostra teoria !)
volgarita, che andrebbe scritto volgarità, ma possiamo anche supporre di non usare gli accenti.
Se l’ordine non è importante, può non essere immediato distinguere parole di fatto equivalenti (vero?) ed
è quindi opportuno introdurre un ordine standard (perché non chiamarlo, in italiano invece che in inglese,
canonico?). L’ordine canonico più ovvio è quello alfabetico: le tre parole viste sopra diventano aagilortv,
che potrebbe essere la sigla di una nuova emittente televisiva…
Se abbiniamo i due esempi, ossia consideriamo tabù sia il disordine (ossia l’ordine non alfabetico) che le
doppie, che cosa otteniamo? Otteniamo una classe importantissima di linguaggi, o meglio di “oggetti”
matematici che di solito vediamo in un altro contesto e con altro nome: gli insiemi!
Questo è precisamente quello che vogliamo fare: ritrovare vecchi concetti in forma nuova, o ricavarne di
nuovi in un contesto diverso da quello del libro, un contesto comune a tutti i concetti (per quelli almeno che
riusciremo ad accomunare): quello dei linguaggi formali (possibilmente volgari). Con qualche vantaggio
1
magari: l’insieme {a, b, c, d} noi lo denotiamo semplicemente con abcd!
L’idea di trascurare l’ordine può sembrare contraddittoria con l’idea stessa di parola (perché non usare
allora direttamente gli insiemi?). Le parole hanno però il vantaggio di poter rappresentare quasi ugualmente
bene il caso in cui l’ordine importa e quello in cui non importa (anche con eventuali ripetizioni di simboli,
che richiederebbero multinsiemi anziché insiemi). Se l’ordine non importa possiamo pensare di avere tutti gli
anagrammi di una data parola: aagilortv, travaglio, giravolta, volgarita, …, oppure di escludere o
considerare tabù tutti gli anagrammi non canonici travaglio, giravolta, volgarita, ….
Un concetto nuovo abbinato a parole senza ripetizioni (ma in cui l’ordine in generale conta) è quello di
parola semplice: nella teoria dei linguaggi, anche se la terminologia non è sempre del tutto standard, una
parola si dice semplice se non contiene ripetizioni, ossia se tutti i suoi simboli sono distinti. Quindi la parola
alla non è semplice (c’è una doppia l) ma neppure ala (la a è ripetuta). Le parole agilortv (senza la doppia a
iniziale) e gilortva sono semplici (e distinte). Un linguaggio semplice è un linguaggio (magari
complicatissimo) in cui tutte le parole sono semplici.
2
Un esempio serio e (moderatamente) complesso
Forse vi è capitato di assistere a qualche incidente d’auto occorso nei pressi del Dipartimento:
quell’incrocio ha un dannato bisogno di un semaforo! Progettare i cicli di funzionamento di un semaforo per
un incrocio un po’ più complicato di quello di cui stiamo parlando (con una confluenza di più vie, per
esempio) può non essere facile e richiedere una metodologia opportuna per evitare di incorrere in errori o
dimenticanze.
Usereste, per esempio, i nomi delle vie (“corso di Porta Vigentina”) o piuttosto una sola lettera per
indicare una via? E non vi sembra conveniente indicare semplicemente con AB il flusso dei veicoli che
transitano dalla via A alla via B (diverso dal flusso BA, magari impossibile per via di un senso unico)? E se
il flusso AB interseca il flusso CD, magari è opportuno considerare tabù la parola ABCD, per esprimere il
rischio di collisioni tra i due flussi.
Allora non è più soltanto un gioco di parole, ma uno strumento di progettazione. Ed è magari conveniente
riconoscere le caratteristiche di questi strumenti e il fatto che si tratta, in realtà, di una classe di strumenti ben
nota e ricca di applicazioni, superando marginali difficoltà di interpretazione. Vediamo.
Abbiamo già visto un esempio in cui le “parolacce” erano parole di due soli caratteri (uguali): se la
parolaccia è di un solo carattere, tanto vale eliminarlo dall’alfabeto, quindi il caso di due caratteri è il primo
interessante. Un linguaggio in cui le parolacce sono solo parole di due caratteri… potrebbe esservi già
familiare in un altro contesto. Un tale linguaggio è un criptomorfismo (“una struttura sotto mentite spoglie”:
comunque questo termine ve lo potete dimenticare ) di un grafo: i caratteri si chiamano di solito vertici e le
parolacce lati o archi!
2
Riprendendo l’esempio del semaforo, abbiamo associato alle vie dei caratteri (incidentalmente maiuscoli,
per adeguarci alla notazione del libro a cui rimandiamo per i dettagli dell’esempio: Aho, Hopcroft, Ullman,
Data Structures and Algorithms, Addison-Wesley, 1983; a proposito dei problemi con le doppie, nella
bibliografia di questo volume almeno in un caso il buon Fibonacci è diventato Fibonnaci) e quindi i vertici di
un grafo. Poi abbiamo accennato ai flussi veicolari dalla via A alla via B, denotati con AB, che saranno
quindi archi del grafo.
Solitamente si chiamano archi le parolacce (attenzione a non prendere per canonica la nostra disinvolta
terminologia!) nei grafi orientati, in cui l’ordine è importante e non è detto che la presenza dell’arco AB
implichi la presenza anche dell’arco BA: potrebbe esserci un divieto di svolta da B verso A!
Nei grafi… e basta, detti anche grafi non orientati, le parolacce non sono ordinate e quindi AB vale
quanto BA: in questo caso si preferisce denominare lati le parolacce, che risultano insiemi di due vertici. O
no? Ci potrebbe essere AA? In qualche caso ciò potrebbe risultare significativo, e il lato si chiamerebbe
cappio, ma nell’esempio del semaforo (e quasi sempre) non lo è e si preferisce considerare grafi senza cappi,
detti anche grafi semplici.
Poiché queste note propongono una sorta di ginnastica mentale per passare agilmente da strutture
concrete ad astratte, e riconoscere le strutture mascherate da altre strutture (i criptomorfismi), facciamo
qualche passo avanti. Per il semaforo siamo partiti etichettando le vie con opportune etichette (caratteri
maiuscoli = vertici del grafo), poi i flussi veicolari (coppie di etichette = archi del grafo), ma in realtà ci
interessano solo i flussi veicolari compatibili o incompatibili, ossia che possono svolgersi simultaneamente
senza rischio di collisioni, oppure no.
Possiamo quindi passare a un nuovo grafo in cui questa volta i vertici sono i flussi (ossia gli archi del
vecchio grafo) e i lati sono le coppie di flussi incompatibili (potevamo scegliere i compatibili, ma quelli tabù
sono quelli importanti, quelli che creano gli incidenti). Ora il grafo non è più orientato: due flussi o sono
compatibili o non lo sono, indipendentemente dall’ordine in cui li consideriamo. Il fatto che a ciascun
vertice-flusso non corrisponda più un unico simbolo, ma
due, è scomodo ma irrilevante.
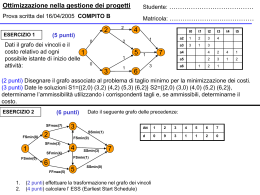
Giusto per essere concreti, ecco qui a lato il grafo
preso dal libro citato.
Torniamo al nostro semaforo: possiamo far muovere
un flusso veicolare alla volta, il che è certamente molto
sicuro. Ma nell’esempio del libro, neanche troppo
complesso, i flussi sono 13. Avete mai misurato quanto
dura il rosso a un semaforo? O avete mai provato tre
minuti di silenzio per qualche commemorazione? Non li
fa mai nessuno! Tre minuti sono eterni!!
3
Quindi il problema è quello di minimizzare il numero di cicli semaforici necessari: assegniamo un ciclo
semaforico (un verde, per intenderci) a un flusso e ad altri flussi compatibili. Vincolo: non possiamo mettere
nello stesso ciclo flussi incompatibili. Obiettivo: minimizzare i cicli dando il verde, prima o poi, a tutti.
Metafora: coloriamo i vertici-flussi del grafo, ovvero le nostre parole di due simboli, col vincolo che paroleflussi incompatibili non possono avere lo stesso colore. Vogliamo colorare il grafo in modo che vertici
adiacenti, ossia incompatibili, abbiano colori diversi, e usare il minimo numero di colori.
I colori non hanno niente a che fare col verde/rosso/giallo del semaforo, ma ciascun “colore” individua un
ciclo (non assegnate un significato rigido al termine “colore”: ginnastica, elasticità!). Useremo spesso,
metaforicamente, i colori.
Se vogliamo tornare alle parole, dobbiamo formare
“belle” parole colorate, che non contengano parolacce.
Le “belle” parole del libro citato corrispondenti ai 4 cicli
semaforici individuati sono AB.AC.AD.BA.DC.ED,
BC.BD.EA.BA.DC.ED,
DA.DB.AD.BA.DC.ED,
EB.EC.EA.BA.DC.ED: nessuna contiene parolacce
come AB.BC o DA.EC (abbiamo usato un punto per
separare i vertici, solo come aiuto al lettore).
Esercizio 1. Provare a ricostruire il grafo dalla
soluzione, ossia a trovare tutte (e sole?) le parolaccelati-incompatibilità: la ricostruzione non è univoca!
Esercizio 2. Come si può procedere per ottenere la
colorazione descritta sopra?
Esercizio 3. Perché il sottografo AC.BD.EB.DA ci garantisce che abbiamo scoperto una colorazione
minima, ossia che il grafo non si può colorare con meno di 4 colori?
Riflettiamo su quello che abbiamo fatto. Siamo partiti da un problema concreto (il semaforo), abbiamo
cercato di formulare un modello astratto del problema (parole e flussi tabù), abbiamo scoperto che la
struttura dei dati, opportunamente interpretata, è ben nota (i grafi), e siamo quindi pervenuti a un problema
teorico anch’esso ben noto, quello della colorazione (minima) dei grafi. A questo punto possiamo
legittimamente sperare che il problema sia già stato risolto in generale, e quindi usare algoritmi risolutivi noti
o addirittura programmi già pronti in qualche libreria di programmi.
La situazione è proprio questa, anche se purtroppo il problema della colorazione minima è noto per essere
un problema difficile, per il quale non si conoscono (e verosimilmente non esistono) in generale algoritmi
risolutivi efficienti. I (molto particolari) grafi di intervalli, per esempio, si colorano facilmente: vedere
l’esercizio 16.1-3 del libro. Alla fine del corso il concetto di efficienza dovrebbe essere perfettamente chiaro:
per ora può restare abbastanza oscuro.
4
3
La volgarità è ereditaria?
Una parola che contiene una parolaccia (“scazzottata”) è anch’essa una parolaccia? Torniamo ai nostri
grafi. Abbiamo (arbitrariamente) deciso che i lati sono parolacce. Che dire di una parola in cui ogni coppia di
simboli adiacenti è una parolaccia: la chiameremo superparolaccia? Potremmo: di fatto, in teoria dei grafi si
chiama semplicemente un cammino, perché la metafora non è quella delle parolacce, ma quella dell’arco AB
pensato come cammino dal vertice A al vertice B, e se c’è anche l’arco BC allora ABC sarà il cammino da A
a C passante per B, e così via. ABABABC potrebbe essere il cammino di un ubriaco, e anche questo ha una
sua tradizione scientifica (i cammini casuali, il moto browniano…). Se il cammino non ha vertici ripetuti si
dice semplice: infatti è espresso da una parola semplice (talvolta la terminologia è coerente!).
Che cosa succede se non solo ABCD è un cammino (semplice), ma tutti suoi anagrammi lo sono? Tutti i
vertici nel cammino devono essere collegati da un lato: abbiamo allora quella che in teoria dei grafi si
chiama una cricca, un sottografo completo, dove completo indica appunto il collegamento di ciascuna coppia
di vertici. Il sottografo AC.BD.EB.DA del semaforo è una cricca!
Vi piacciono le parolacce di quattro simboli (l’equivalente inglese di parolaccia è four-letter word. Un
motivo in più per imparare l’inglese…)? OK! Togliamo ogni limite di lunghezza, ma restiamo tra parole
semplici e non ordinate (insiemi).
Che cosa succede se fissiamo un certo numero di parolacce e diciamo che tutte quelle che le contengono
sono a loro volta parolacce? Quali sono le parole “per bene” o semplicemente “belle”?
Abbiamo bisogno di un esempio: torniamo alle minuscole e prendiamo una parolaccia di 3 lettere, abc, e
supponiamo che il nostro alfabeto abbia solo le 4 lettere a, b, c, d. Tutte le parole di una o due lettere sono
belle, così come abd, acd, bcd (non ce ne sono altre di 3 lettere: sono “parole non ordinate” ossia insiemi,
scritti canonicamente in ordine alfabetico). Le parolacce sono abc e abcd.
Quale situazione potrebbe modellare questo esempio? Forse quella di quattro simpatici ragazzini, Ada,
Bruno, Carlo e Dina, in genere tranquilli, mentre la combinazione Ada-Bruno-Carlo è esplosiva, come sanno
bene le madri che evitano di metterli insieme. Si tratta di una sorta di incompatibilità (ricordate i flussi al
semaforo?) a tre, invece che a coppie.
Se tutte le parole che contengono parolacce sono anch’esse parolacce, è pure vero che tutte le parole
contenute in belle parole sono belle. Anche questo tipo di struttura è ben nota: si tratta dei cosiddetti sistemi
d'indipendenza o complessi simpliciali astratti. Basta chiamare insiemi indipendenti le belle parole e
viceversa insiemi dipendenti le brutte. Un’alternativa potrebbe essere quella di parlare di sistemi ereditari:
l’indipendenza è ereditata dai sottoinsiemi (se abd è indipendente, lo sono anche a, ab, bd, …), la
dipendenza dai superinsiemi (se abc è dipendente lo è anche abcd).
Ginnastica! Gli insiemi di vertici di un grafo in cui nessuna coppia di vertici è unita da un lato si
chiamano… insiemi indipendenti del grafo. Ma anche le cricche ereditano la “cricchicità”: un sottoinsieme
dei vertici di una cricca è ancora una cricca!
5
Se passiamo dagli insiemi alle parole in cui l’ordine conta arriviamo al concetto di linguaggio ereditario:
l’appartenenza al linguaggio è ereditata dai prefissi di ogni parola. I prefissi sono naturalmente… quelli che
vi aspettate che siano: tutte le porzioni iniziali della parola, inclusa l’intera parola e la parola vuota,
l’analogo dell’insieme vuoto . La parola vuota avrà anch’essa diritto a un simbolo tutto suo: di solito  o .
Quale sarà dunque, per esempio, il linguaggio ereditario generato dalla sola parola volgarita? Sarà il
linguaggio L costituito da tutti i prefissi, ossia L = {, v, vo, vol, volg, volga, volgar, volgari, volgarit,
volgarita}.
Riprendiamo ora un vecchio quiz. Sul pianeta Alber è facile stabilire le parentele: i figli aggiungono
semplicemente una lettera in fondo al nome del padre. Per esempio, Bobb è figlio di Bob. Chi tra i seguenti è
lo zio di Bobby?
1)
2)
3)
4)
Bobb
Bobo
Bob
Boh
Che cosa vorrebbe insegnarci il quiz riportato sopra? Forse che è possibile pensare
ai linguaggi ereditari come ad alberi (con radice), e viceversa? Quale linguaggio
assocereste all’albero riportato a lato (non è vietato usare le cifre come simboli
dell’alfabeto!)?
L = {, 3, 32, 324, 321, 3216, 37, 375}. Se vogliamo che la radice (nel nostro caso
il nodo 3) sia etichettata, come tutti gli altri nodi, dovremo avere in L una sola parola di lunghezza 1 (ossia
costituita da un solo simbolo), altrimenti potremmo accontentarci di una radice “anonima” . Inoltre, se
etichettiamo i vertici con simboli differenti, ogni parola dovrà, come qui, terminare con un simbolo diverso
dalle altre: ci occorrono tanti simboli dell’alfabeto quanti sono i vertici.
Ma il linguaggio T = {, 0, 00, 01, 010, 1, 10} definisce la stessa struttura di albero (astraendo dalle
etichette) e usa un alfabeto di cardinalità pari al massimo numero di figli che un vertice può avere: 00 e 01
sono entrambi figli di 0, a sua volta figlio della radice  e prima etichettato con 2, e dobbiamo poter
distinguere ciascun figlio; se 0 avesse 7 figli ci servirebbero (almeno) 7 simboli diversi!
Gli alberi binari possono essere rappresentati astrattamente usando un alfabeto binario, con soli due
simboli, ma, una volta tanto, si attribuisce un preciso significato a ciascuno dei due simboli: figlio destro o
figlio sinistro. Parafrasando parola per parola (anzi, nodo per parola ) la definizione ricorsiva del libro
(appendice B.5.3), un albero binario T è un linguaggio che o è il linguaggio vuoto  (non contiene parole,
neppure la parola vuota) oppure è l’unione (disgiunta) della parola vuota , del linguaggio 0S, con S
sottoalbero sinistro, e del linguaggio 1D, con D sottoalbero destro. Il linguaggio 0S si ottiene premettendo 0
a ciascuna parola di S mentre 1D si ottiene premettendo 1 a ciascuna parola di D, avendo (arbitrariamente)
deciso di indicare con 0 i figli sinistri e con 1 i destri.
6
Nell’esempio visto sopra abbiamo T =  ∪ 0S ∪ 1D con S = {, 0, 1, 10} e D = {, 0}. Il sottoalbero
destro D poi, per esempio, è a sua volta un albero binario: D =  ∪ 0{} ∪ 1. La parola vuota  non si
vede, e quindi 0 = 0, mentre se premettiamo un 1 a… niente, otteniamo ancora niente: 1 = .
4
Parole buone e matroidi
La metafora delle parole più o meno “buone” si presta bene per introdurre un’ulteriore struttura molto
importante nella teoria degli algoritmi così come in matematica combinatoria.
Supponiamo che le parole-insiemi che non contengono parolacce abbiano una proprietà aggiuntiva: prese
due parole di lunghezza diversa, è sempre possibile aggiungere alla parola più corta qualche simbolo
presente nella parola più lunga, in modo tale che la nuova parola sia ancora “buona”. La parola più lunga è
così “buona” da regalare qualche simbolo alla parola più corta, che così cresce! Questa proprietà è dunque
chiamata proprietà di accrescimento, ed è equivalente a una proprietà formulata diversamente che si chiama
proprietà di scambio: il libro non distingue tra le due. Qui la chiameremo anche noi così, anche se è evidente
che non c’è uno “scambio” tra parola lunga e corta: la parola lunga si tiene il suo simbolo e ne regala uno
uguale alla corta, per così dire.
Conosciamo già un esempio, quello con le parolacce abc e abcd: prese le parole ac e abd, per esempio,
possiamo aggiungere ad ac il simbolo d, presente in abd, e ottenere la parola buona acd. Notiamo che non è
detto che tutti i simboli nella parola lunga vadano bene: dobbiamo ovviamente escludere quelli
eventualmente già presenti nella parola corta (a) e forse altri (b), ma ce ne dev’essere almeno uno che la
parola lunga può “regalare” alla corta.
Vediamo un controesempio, ossia un caso in cui la proprietà di scambio non è vera. Supponiamo che le
uniche parole buone di due lettere, sempre sull’alfabeto di quattro lettere, siano ab e cd (ovvero abbiamo 4
parolacce: ac, ad, bc, bd) e prendiamo le due parole b e cd: questa volta non possiamo aggiungere a b nessun
simbolo di cd, perché sia bc sia bd sono parolacce.
Saremmo tentati di chiamare linguaggi buoni quelli in cui la proprietà è presente, ma hanno già un nome
più esotico: greedoidi, dall’inglese greedy = ingordo. La connessione, non tanto ovvia, è con gli algoritmi
greedy. Vedremo più avanti la stretta connessione tra questi algoritmi e le strutture in cui vale la proprietà di
scambio insieme con quella ereditaria che definisce i sistemi d’indipendenza.
Facciamo prima una digressione linguistica (nel senso dei linguaggi naturali). Vorrei far notare come sia
molto diverso scrivere (o dire) “algoritmi greedy” piuttosto che “algoritmi di Greedy” (come ho visto scritto
in un libro!): la seconda forma fa pensare che tali algoritmi prendano il nome da un qualche signor Greedy
che li ha scoperti, ma non è così!
7
Un sistema d’indipendenza che sia anche un greedoide (ossia abbia anche la proprietà di scambio) è
chiamato matroide. Nei matroidi, tutti gli insiemi indipendenti massimali sono anche massimi. Cosa vuol
dire? Semplicemente che le parole-insiemi buone che non possono “ricevere regali”, cioè essere allungate (le
chiamiamo massimali), devono avere la stessa lunghezza massima: se infatti esistesse una parola buona più
lunga, questa dovrebbe poter regalare nuovi simboli alla parola più corta.
Sarà bene notare che nel controesempio visto sopra la parola b non è massimale: infatti può essere
allungata a formare ab, e ab e cd sono le uniche parole indipendenti massimali e sono anche massime.
Eppure la proprietà di scambio non valeva e quindi il controesempio non era un greedoide e dunque neanche
un matroide. C’è una contraddizione? Se pensate di sì dovreste riflettere sulla differenza tra condizione
necessaria e sufficiente.
Nei matroidi, è necessario che tutti gli insiemi indipendenti massimali siano anche massimi, ma non è
sufficiente. Quindi, se in un sistema d’indipendenza troviamo insiemi indipendenti massimali di cardinalità
diverse, allora certamente non è un matroide, ma se, come sopra, non ne troviamo, non è ugualmente detto
che sia un matroide. La proprietà massimale = massimo è una conseguenza della proprietà di scambio, ma
non viceversa: la proprietà di scambio implica qualcosa in più, come spiegheremo più avanti.
Vorremmo che la differenza tra massimale e massimo fosse ben chiara. Riprendiamo gli alberi come
linguaggi ereditari: le parole del linguaggio rappresentano i rami dell’albero (o i tratti di ramo dalla radice
fino a un certo nodo) e le foglie (o i rami completi) corrispondono alle parole massimali, che non sono
prefissi più corti di altre parole del linguaggio. Nell’esempio sopra, 324 e 375 sono massimali, mentre 321,
per esempio, non lo è. Le parole massime (nell’esempio 3216, ma non è detto che il massimo sia unico)
corrispondono ai rami più lunghi, la cui lunghezza definisce l’altezza dell’albero.
Analogamente, abbiamo visto insiemi indipendenti e cricche nei grafi: una cricca è massimale quando
ogni vertice esterno alla cricca è scollegato da qualche vertice della cricca. E tuttavia il grafo può ben
contenere “altrove” una cricca più grande e massima! Nel grafo del semaforo il vertice isolato BA è una
(piccola) cricca massimale, mentre AC.BD.EB.DA è una cricca massima (visto che siamo riusciti a colorare
tutto il grafo con 4 colori)!
Abbiamo anticipato in maniera alquanto informale e forse imprecisa parecchi concetti che riprenderemo
in seguito con maggiore rigore. Qui volevamo mostrare come questi concetti, a prima vista eterogenei,
possano essere ritrovati in maniera abbastanza naturale in un contesto omogeneo legato ai linguaggi formali.
5 Giochi di parole
Vogliamo concludere con un altro quiz, che speriamo vi aiuterà a imprimere in memoria le caratteristiche
di una struttura di dati assai importante. Non daremo le risposte.
Sul pianeta Ip i nomi delle persone di una data famiglia formano un linguaggio ereditario, contenente
tutti i prefissi del nome dell’ultimo nato. Di conseguenza, i nomi hanno tutte le lunghezze da 1 sino alla
8
lunghezza massima. Ma la caratteristica davvero peculiare è che, detta l(x) la lunghezza del nome x, il nome
del genitore di x è costituito dai primi l(x)/2 caratteri di x, ossia è il prefisso di x di lunghezza pari alla metà
della lunghezza di x, troncata alla parte intera. Il nome del genitore di Filippo, per esempio, è Fil.
Ed ecco il quiz!
1) Filippo ha un fratello?
2) Come si chiama il nonno di Filippo? e lo zio?
3) Ricostruire l’intero albero genealogico di Filippo.
4) In generale, su Ip, quanti figli ha ciascun genitore? Ci possono essere eccezioni?
5) Quanto sono lunghi i nomi dei figli di un genitore?
6) Esistono i sessi sul pianeta Ip?
Solo dopo aver risposto ai quesiti, ritrovate nel testo la struttura di dati corrispondente, che vi aiuterà
anche a controllare le risposte e risolvere eventuali dubbi.
9