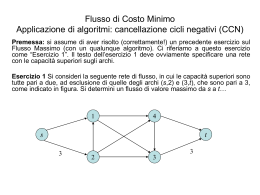
Cos'è la Ricerca Operativa
partendo da basi teoriche
disciplina che tratta dello
sviluppo e
dell'applicazione di
metodi scientifici
costruzione di modelli
concreti
confronto diretto con la
realtà
permettendo di
effettuare scelte
razionali
Un po' di storia...
Nasce durante la seconda guerra
mondiale.
al termine del conflitto"riconversione"
dell'approccio orientandolo verso
problematiche di tipo civile.
In Italia, un gruppo di ricercatori, tecnici
e dirigenti d'azienda fondò l'AIRO avente
lo scopo di promuovere studi teorici ed
applicazioni pratiche della disciplina.
Campi di applicazione
Può essere utilizzata in:
teoria dei giochi
(problemi di
decisione in
condizioni
competitive)
teoria dei grafi
(utilizzata per le reti
di comunicazione)
teoria delle scorte
(stoccaggio di
magazzino)
programmazione
lineare (pianificazione
del problema)
programmazione
dinamica
(pianificazione delle
vendite)
programmazione
reticolare (gestione
progetti);
teoria delle code (per
gestire i problemi di
traffico)
Viene applicata in Logistica, Trasporti, Finanza, Gestione delle Risorse Umane, Gestione
dei Servizi Sanitari, Telecomunicazioni, Progettazione Industriale, Data Mining, Bioinformatica
Ottimizzazione
Problemi formalizzabili come
minimizzazione e massimizzazione
di una funzione sottoposta a vincoli.
Gli altri casi sono riconducibili ad
un modello di Programmazione
Matematica.
Programmazione Lineare
Modelli di Programmazione Lineare
Allocazione ottima di
risorse
Miscelazione
Trasporto
Metodo grafico
Rappresentazione
geometrica del
dominio dei vicoli.
Teorema
fondamentale della PL:
Ottimo sui vertici.
Determinazione
soluzione ottima.
Esempio di problema di PL
Algoritmo del simplesso
L'Algoritmo del simplesso è un metodo per
risolvere problemi di programmazione lineare.
Si vuole massimizzare o minimizzare una
funzione lineare con delle restrizioni (vincoli)
anch'esse lineari per i valori delle variabili, che
possono assumere valori positivi.
I vincoli definiscono la regione ammissibile.
Nel caso della programmazione lineare la regione
ammissibile è un insieme poliedrico, il quale può
essere vuoto, limitato o illimitato.
L'algoritmo del simplesso è in grado di determinare
di che tipo di poliedro si tratta e trova la soluzione
ottima, che è un vertice del poliedro.
George Dantzig
(Portland, Oregon, USA, 8
novembre 1914 – Palo Alto,
California, USA, 13 maggio 2005)
Come funziona il Simplesso
8 x1  4 x2  2 x3 min
1x2  0,375 x4  0,25 x5  3

1x3  0,046 x4  0,25 x5  1
1x  0,046 x  0,25 x  9
4
5
 1
X1
X2
Caso di partenza
Si genera la prima tabella con i dati del
sistema.
X3
X4
X5
X1 8
1
0
0
-0,046
0,25
9
X2 4
0
1
0
-0,375
-0,25
3
X3 2
0
0
1
0,046
-0,25
1
Cr
8
4
2
0
0
88
Δr
0
0
0
2,25
-0,5
X1
X2
X3
X4
I ∆r si calcolano moltiplicando il
coefficienti delle variabili in base per la
rispettiva colonna del ∆r, sottraendo il
risultato al Cr.
Il medesimo ragionamento si applica
alla Z.
X5
X2 4
1
1
0
-0,042
0
12
X3 2
1
0
1
0
0
10
X5 0
4
0
0
-0,18
1
36
Cr
8
4
2
0
0
68
Δr
2
0
0
1,68
0
Dato che il problema è di minimo la
variabile ad entrare in base è quella con
il ∆r minore.
Si arriva alla soluzione finale quando
tutti i ∆r sono maggiori di zero.
Algoritmo di Dijkstra
L'algoritmo di Dijkstra permette di trovare i cammini
minimi in un grafo.
In particolare l'algoritmo può essere utilizzato per trovare:
 cammino minimo che unisce due nodi del grafo,
 quelli che uniscono un nodo d'origine a tutti gli altri
 tutti i cammini minimi da ogni nodo ad ogni altro nodo.
Tale algoritmo trova applicazione in molteplici contesti.
Per esempio permette, dato un grafo che rappresenta
un'ipotetica "mappa" di condotte di
approvvigionamento idrico di una città. Esempio
analogo può essere fatto considerando il "problema" di
trovare il collegamento meno dispendioso, in termini di
potenza dissipata, nella realizzazione di un circuito
elettrico.
Edsger Dijkstra
(Rotterdam, 11 maggio 1930 Nuenen, 6 agosto 2002)
Come funziona Dijkstra
Caso di partenza
•Ogni nodo ha, all'inizio potenziale ∞
•Il nodo di partenza ha potenziale 0
•Ogni volta si sceglie il nodo con potenziale minore e lo si rende
definitivo e si aggiornano i nodi adiacenti
•Il potenziale di un nodo è dato dalla somma del potenziale del
nodo precedente + il costo del collegamento
•Non si aggiornano i potenziali dei nodi resi definitivi
•I potenziali definitivi indicano la distanza di quel nodo da
quello di partenza
•Quando si aggiorna il potenziale di un nodo si lascia quello
minore
L’algoritmo partendo dal nodo di origine trova ad ogni
passaggio il nodo adiacente con peso minore e lo aggiunge alla
coda, e aggiorna man mano il peso dei nodi adiacenti.
Una volta raggiunto il nodo di arrivo è sufficiente ripercorrere
all’indietro il percorso individuato per avere il percorso minimo.
Funzioni di due variabili
z  f ( x, y )
R2
Insieme di definizione
Linee di livello
Limite
Continuità
lim f ( x, y )  l
Derivate parziali de primo ordine
x  x0
y  y0
Derivate parziali del secondo ordine
Massimi e minimi relativi
Massimi e minimi condizionati
Fonti utilizzate
www.matematicamente.it
www.wikipedia.org