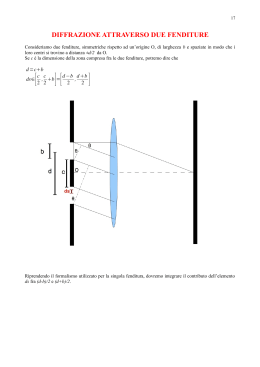
Ruggero Caravita, Giacomo Guarnieri, Roberta Lanfranco – Gruppo Me7 1
Interferenza e diffrazione
Interferenza e diffrazione
Relazione sperimentale
Lo scopo dell’esperienza è quello di indagare i fenomeni di interferenza e
diffrazione di un raggio di luce monocromatico misurando la lunghezza d’onda
della luce incidente, il passo di reticoli di varia natura e l’ampiezza di differenti
fenditure. Le ultime due grandezze (passo dei reticoli e ampiezza delle
fenditure) saranno indagate anche in contemporanea, esaminando reticoli
d’interferenza le cui fenditure abbiano ampiezza non trascurabile.
Apparato sperimentale
L’apparato di misura è atto alla riuscita dell’esperienza è composto da:
un laser, ossia un fascio molto coerente e ben collimato, di luce monocromatica verde;
un supporto per i diaframmi con i reticoli e le fenditure;
una lente divergente, posta tra il laser e il support;
una fotocellula con micrometro, posta su un carrello dotato di grado di libertà lungo la
direzione ortogonale alla direzione di propagazione del raggio;
uno schermo per raccogliere la figura di interferenza/diffrazione;
un software collegato alla fotocellula, atto alla raccolta di tutti i dati di campionamento che
la fotocellula rileva durante la traslazione e memoria dei valori di intensità relative.
Presupposti teorici
Misura dei massimi di interferenza e dei minimi di diffrazione
I fenomeni di interferenza e diffrazione di un’onda elettromagnetica hanno luogo ogniqualvolta
viene posto un ostacolo sul suo cammino ed evidenziano l’insufficienza dell’utilizzo del solo
modello geometrico di descrizione della luce, a favore di uno misto ad un modello anche
ondulatorio. Il fenomeno di interferenza più in particolare ha luogo quando due onde
elettromagnetiche sono emesse da sorgenti coerenti, sincrone e polarizzate nello stesso piano,
mentre il fenomeno di diffrazione si verifica quando la presenza di diaframmi limita parzialmente il
percorso:o ogni punto del nuovo fronte d’onda secondario può essere interpretato secondo il
modello di Huyghens-Fresnel come origine di una successiva onda sferica (o circolare) infinitesima.
Sfruttando il principio di sovrapposizione, è possibile studiare i due fenomeni indipendentemente
l’uno dall’altro sulla stessa figura.
Le tipologie di diffrazione sono sostanzialmente due: quella di Fraunhofer e quella di Fresnel, che
differiscono per il fatto che nel primo caso la sorgente è considerata posta a distanza infinita dal
diaframma, mentre nel secondo caso a distanza finita. L’utilizzo della lente e il posizionamento
della sorgente nel suo fuoco permettono di ritenere soddisfatte le ipotesi di Fraunhofer, e in
questo esperimento ci si limiterà a studiare fenomeni di questo tipo.
E’ noto in letteratura che la figura di interferenza generata da un reticolo incide sull’intensità
secondo la legge
Pagina 1 di 6
Ruggero Caravita, Giacomo Guarnieri, Roberta Lanfranco – Gruppo Me7 2
Interferenza e diffrazione
dove d è la distanza fra le fenditure (nota anche come passo del reticolo), λ la lunghezza d’onda
della luce monocromatica incidente, θ l’angolo del raggio considerato a partire dal centro di una
qualunque delle frange (θ è costante per tutti solo nel caso della diffrazione di Fraunhofer),
presentando dei massimi in coincidenza di
mentre il fenomeno di diffrazione interviene sempre sulla stessa con un fattore pari a
presentando dei minimi in corrispondenza di
Si può dimostrare che la diffrazione è il fenomeno modulante dell’intensità (ovvero fornisce la
forma della figura), la quale è inframezzata dall’andamento sinusoidale dell’interferenza che agisce
da portante. Ciò è coerente con il fenomeno di interferenza in quanto tale se considera costante il
termine modulante della diffrazione. Nonostante la distanza della sorgente sia abbastanza
maggiore della larghezza angolare della figura di interferenza, si è preferito non ricorrere
all’approssimazione di piccoli angoli, al fine di minimizzare eventuali errori sistematici.
Procedimento sperimentale
Misura della lunghezza d’onda del laser
Si inserisce sul supporto un reticolo di passo noto d = 617 frange/mm e, misurando la posizione di
n massimi principali, si applica la (2). Al fine di ridurre gli errori di lettura, è stata usata l’accortezza
di misurare per ogni massimo registrato la coppia di posizioni simmetriche rispetto al massimo
centrale, per poi mediare ogni posizione.
In Tabella 1 sono riportate le misure della lunghezza d’onda
Dist. Schermo-Reticolo
50,6 cm
39,7 cm
63,7 cm
79,4 cm
20,6 cm
Media
λ media
σ
0,3
0,3
0,3
0,4
0,2
Dist. Max-Max
35,7 cm
28,2 cm
44,9 cm
55,8 cm
14,5 cm
σ
0,1 cm
0,1 cm
0,1 cm
0,1 cm
0,1 cm
Lunghezza d'onda λ
σλ
539,2 nm
542,4 nm
538,7 nm
537,3 nm
538,1 nm
4,1 nm
5,2 nm
3,2 nm
3,3 nm
7,4 nm
538,8 ± 1,8 nm
Pagina 2 di 6
Ruggero Caravita, Giacomo Guarnieri, Roberta Lanfranco – Gruppo Me7 3
Interferenza e diffrazione
Lunghezza d'onda (nm)
550
545
540
535
530
525
Tabella 1: Misura della lunghezza d'onda del laser e confronto grafico dei valori per la compatibilità
Poiché le misure risultano compatibili fra loro entro 1.98σ il valore finale della lunghezza d’onda è
la media pesata delle misure.
Misura del passo del reticolo di diffrazione e dell’ampiezza delle fenditure
Dato che la fotocellula che verrà usata per acquisire i dati è in grado di rilevare solo intensità
relative, la si deve prima di tutto calibrare sul valore minimo, assunto come “zero”. Si procende
quindi all’ inserimento di vari diaframmi differenti sul supporto, con la rispettiva raccolta dati: la
fotocellula, mossa dall’albero di un micrometro lungo la guida ortogonale alla direzione di
propagazione del fascio, rileva e invia al computer coppie di dati del tipo [posizione, intensità] . Per
aumentare la mole di dati a nostra disposizione e ridurre quindi eventuali errori, si è ripetuto l’iter
di raccolta dati per ogni tipologia di reticolo facendo variare tre volte la distanza del reticolo dalla
fotocellula (modificando quindi il parametro L delle formule per i massimi di interferenza e per i
minimi di diffrazione).
OSS: La vite micrometrica collegata alla fotocellula presenta ovviamente un po’ di gioco, per cui si
è avuta l’accortezza di farla sempre partire da un punto vicino ma non coincidente allo zero della
stessa.
Una volta completata l’acquisizione di una serie di dati, si è immediatamente palesata
all’attenzione la difficoltà di individuare con una precisione sufficiente i minimi di diffrazione,
molto disturbati dal “rumore” di fondo rappresentato dalla luminosità limitrofa (Grafico 1).
Pagina 3 di 6
Ruggero Caravita, Giacomo Guarnieri, Roberta Lanfranco – Gruppo Me7 4
Interferenza e diffrazione
Intensità rilevata
0,6
Intensità rilevata (W/m2)
0,5
0,4
0,3
0,2
0,1
0
0
5
-0,1
10
15
20
25
30
25
30
Tempo dall'inizio dell'esperimento (s)
3
Derivata dell'intensità rispetto al tempo
Variazione dell'intensità (W/(s*m2))
2
1
0
0
5
10
15
20
-1
-2
-3
Tempo dall'inizio dell'esperimento (s)
Grafico 1: Presa dati di prova e sua derivata rispetto al tempo calcolata con gli incrementi finiti
Dall’esame del grafico (soprattutto dal grafico della derivata a incrementi finiti calcolata come )
appare evidente che il rilevatore di intensità rilevi l’intensità a scalini non trascurabili (stimati
intorno a 0,010 W/m2). Il problema dell’estrazione dei massimi e dei minimi non è banale, poiché
non è assolutamente evidente dove collocarli in modo rigoroso.
Pagina 4 di 6
Ruggero Caravita, Giacomo Guarnieri, Roberta Lanfranco – Gruppo Me7 5
Interferenza e diffrazione
L’unica soluzione che è praticabile per non commettere errori grossolani nella determinazione dei
minimi è realizzare un software che applichi un filtro medio o filtro gaussiano ai dati (il filtro altera
la posizione dei singoli punti sostituendo la media pesata di N punti pari a sinistra e destra di esso),
quindi proceda ad estrarre i massimi e i minimi cercando gli zeri della funzione derivata e
determinandoli eseguendo una regressione lineare nei punti di prossimità allo zero. In Grafico 2 è
dimostrata l’efficacia del filtro gaussiano sui dati prima mostrati per l’identificazione di massimi e
minimi; il grafico non è più normalizzato ne tanto meno si conservano le altezze dei picchi, ma
questo è indifferente ai nostri scopi.
Intensità rilevata
0,6
Intensità rilevata (W/m2)
0,5
0,4
0,3
0,2
0,1
0
0
5
10
15
20
25
30
Tempo dall'inizio dell'esperimento (s)
2,50E-02
Derivata dell'intensità rispetto al tempo
Variazione dell'intensità (W/(s*m2))
2,00E-02
1,50E-02
1,00E-02
5,00E-03
0,00E+00
-5,00E-03
0
5
10
15
20
25
30
-1,00E-02
-1,50E-02
-2,00E-02
-2,50E-02
Tempo dall'inizio dell'esperimento (s)
Grafico 2: Serie di dati di esempio con applicato il filtro gaussiano per facilitare l’estrazione dei massimi e dei minimi
Pagina 5 di 6
Ruggero Caravita, Giacomo Guarnieri, Roberta Lanfranco – Gruppo Me7 6
Interferenza e diffrazione
Il sensore resituisce, oltre al dato di tempo, un valore di posizione che è quello che è stato
effettivamente impiegato per ottenere le distanze. Nelle seguenti Tabelle sono sintetizzati i
risultati ottenuti valutando per ciascun set di dati massimi e minimi nel modo mostrato, divisi per
tipologia del reticolo di diffrazione e della distanza.
#Fend dteor
(mm)
1
1
2
0,125
2
0,250
2
0,500
1
1
2
0,125
2
0,250
2
0,500
1
1
2
0,125
2
0,250
2
0,500
ateor
(mm)
0,040
0,080
0,040
0,040
0,040
0,040
0,080
0,040
0,040
0,040
0,040
0,080
0,040
0,040
0,040
L
(m)
1,379
1,379
1,379
1,379
1,379
1,584
1,584
1,584
1,584
1,584
2,000
2,000
2,000
2,000
2,000
x-x
(mm)
36
19
38
37
34
40
24
43
42
40
53
27
55
55
55
σx-x
(mm)
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
dsper
(mm)
0,139
0,266
0,496
0,136
0,250
0,551
0,136
0,263
0,540
σd
(mm)
0,006
0,021
0,074
0,004
0,012
0,060
0,002
0,007
0,029
X-X
(mm)
10,7
5,6
3,0
12,6
6,8
3,1
15,9
8,2
4,0
σX-X
(mm)
0,2
0,2
0,2
0,2
0,2
0,2
0,2
0,2
0,2
asper
(mm)
0,041
0,078
0,039
0,040
0,044
0,043
0,071
0,040
0,041
0,043
0,040
0,080
0,039
0,040
0,039
σa
(mm)
0,005
0,002
0,005
0,005
0,006
0,004
0,010
0,003
0,003
0,004
0,002
0,006
0,002
0,002
0,002
Tabella 2: Tabella delle misure svolte, comprensiva di dteor e ateor teoriche, distanza L del laser, distanza x-x minimo
minimo, distanza X-X massimo massimo, dsper e asper sperimentali con relativi errori di misura.
Conclusioni
I valori ottenuti sono compatibili con la teoria e dimostrano la validità del metodo per estrarre i
massimi e minimi. Tale strumento non è perfetto: non è in grado, per esempio, di dare una stima
valida delle distanze minimo minimo e massimo massimo nel caso dei reticoli di diffrazione, in
quanto una qualunque media sui dati altera significativamente il quadro dei massimi e dei minimi.
Un eventuale miglioramento del software dovrebbe senz’altro comprendere un sistema per
stimare la lunghezza d’onda del laser con maggiore precisione, ricorrendo alla grande quantità di
dati presi con setup molto diversi fra loro; un metodo iterativo potrebbe essere una scelta, oppure
una massimizzazione del grafo a più dimensioni di χ 2 intorno ai valori teorici per ottenere il miglior
fit di tutte le variabili contemporaneamente.
Pagina 6 di 6