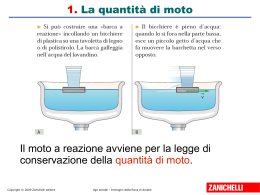
Unità 11
La quantità di moto e il
momento angolare
Copyright © 2009 Zanichelli editore
1. La quantità di moto
Il moto a reazione avviene per la legge di
conservazione della quantità di moto.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Il vettore quantità di moto
Il vettore quantità di moto di un corpo è dato dal
prodotto della massa per il vettore velocità.
•
ha la stessa direzione e verso del vettore velocità;
•
è proporzionale alla velocità
e alla massa (a parità di v, p è maggiore per un
treno che per un'automobile).
•
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
2. La conservazione della quantità di moto
Consideriamo un fenomeno che simula
“l’esplosione” di un corpo in due frammenti:
p totale era zero all'inizio e rimane zero alla fine.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
La conservazione della quantità di moto
Consideriamo ora i due frammenti di massa
l'una doppia dell'altra:
p totale era zero all'inizio e rimane
zero alla fine.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
La conservazione della quantità di moto
Quindi la quantità di moto di ciascun corpo
cambia, mentre la quantità di moto totale del
sistema rimane costante.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
La legge di conservazione della quantità di moto
In termini più generali si esprime:
se su un sistema non agiscono forze esterne, la
quantità di moto totale del sistema si conserva.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
3. L'impulso di una forza
Definiamo impulso di una forza F il vettore
prodotto della forza per l'intervallo di tempo
durante il quale essa agisce:
L'impulso è legato alla variazione di p:
ovvero
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Il teorema dell'impulso
Dalle formule precedenti si ricava il teorema
dell'impulso:
ovvero
La variazione della quantità di moto che una forza
determina è uguale all'impulso della forza stessa.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Minimizzare la forza d'urto
Quando si subisce un urto, c'è una grossa
variazione di p.
Poiché
, Furto=p/t.
Se il tempo dell'urto t è più lungo allora la Furto è
più piccola.
Per aumentare t , nelle cadute si piegano le
gambe.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Minimizzare e massimizzare la forza d'urto
Nelle automobili l'intervallo di tempo t viene
aumentato (e quindi Furto minimizzata) utilizzando
gli airbag e carrozzerie deformabili.
Nel karate, un brevissimo t massimizza Furto e
consente di spezzare una pila di mattoni.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
4. I princìpi della dinamica e la legge di conservazione
della quantità di moto
Consideriamo l'interazione di due corpi A e B e
utilizziamo la notazione seguente:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
I princìpi della dinamica e la legge di conservazione
della quantità di moto
Per il III principio della dinamica:
Moltiplicando per t:
Per il teorema dell'impulso si ha:
quindi
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
I princìpi della dinamica e la legge di conservazione
della quantità di moto
La formula precedente si può scrivere:
La conservazione della quantità di moto in un
sistema isolato è conseguenza dei princìpi della
dinamica.
L'emissione di gas dai motori
dell'aereo determina la spinta
in avanti.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Una conferma sperimentale
La foto mostra l'urto di due biglie di massa
diversa:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Una conferma sperimentale
Se rappresentiamo con frecce dello stesso colore
delle biglie le quantità di moto iniziali e finali, si
vede che la quantità di moto totale resta la stessa
prima e dopo l'urto.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
5. Gli urti su una retta
Durante un urto i due corpi che collidono
rappresentano un sistema isolato, quindi la
quantità di moto totale si conserva.
m1, m2: masse
dei corpi

v1, v2: velocità
prima dell'urto

V1, V2: velocità
dopo l'urto

Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Urto elastico
Durante un urto elastico si conservano:
•
la quantità di moto totale;
•
l'energia cinetica totale.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Urto elastico
Se conosciamo le masse di corpi e le velocità
iniziali, possiamo ricavare le velocità finali
risolvendo il sistema:
p1 + p2 = cost.
K1 + K2 = cost.
In cui compaiono due equazioni nelle due
incognite V1 e V2.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Urto completamente anelastico
I due oggetti che collidono rimangono uniti dopo
l'urto:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Urto completamente anelastico
In un urto completamente anelastico V1 = V2 = V:
la velocità finale V è determinata dalla sola legge
di conservazione della quantità di moto.
Si ha
ovvero
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
6. Gli urti obliqui
Caso semplice: due biglie uguali di massa m, di
cui una inizialmente ferma; urto elastico.
Indichiamo con:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Gli urti obliqui
1) Imponiamo la conservazione di p:
dividendo per m:
2) Imponiamo la conservazione di K:
ovvero
Il triangolo ABC è rettangolo.
Dopo l'urto le due biglie hanno velocità
perpendicolari tra loro.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
7. Il momento angolare
Esaminiamo i moti di rotazione.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Il momento angolare
Per descrivere le
momento angolare:
rotazioni
(Il vettore quantità di moto ha
stessa direzione e verso
del vettore velocità.)
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
introduciamo
il
Il momento angolare
Ricordando la definizione di prodotto vettoriale,
L ha:
direzione perpendicolare al piano di r e v;
verso dato dalla regola della mano destra;
modulo L dato dalle formule:
dove  è l'angolo tra i
vettori r e p.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
8. Conservazione e variazione del momento angolare
Il momento angolare totale di un sistema si
conserva se è nullo il momento totale delle forze
esterne che agiscono sul sistema stesso.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica
Conservazione e variazione del momento angolare
Se sul sistema agiscono delle forze che hanno
un momento totale M per un tempo t, la
variazione di L è data da:
M è il momento torcente del sistema, che è in
grado di aumentare o diminuire la velocità di
rotazione.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Corso di fisica