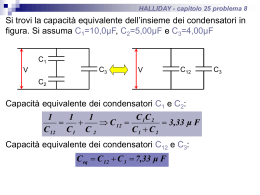
ELETTROSTATICA
+ Carica Elettrica
+ Campi Elettrici
+ Legge di Gauss
+ Potenziale Elettrico
+ Capacita’ Elettrica
ELETTRODINAMICA
+ Correnti
+ Campi Magnetici
+ Induzione e Induttanza
+ Equazioni di Maxwell
+ Onde Elettromagnetiche
Capacita’ elettrica
Cos’e’ un condensatore ?
E’ un dispositivo in grado di immagazzinare la carica elettrica. Svolge un ruolo
importante nella realizzazione tecnica di dispositivi elettronici
Il principio del condensatore aiuta a schematizzare anche altri effetti (fenomeni
METEO di origine elettrostatica)
Prendiamo un conduttore. Quanta carica riusciamo ad immagazzinare ? Qual e’
cioe’ la sua capacita’ ?
Capacita’ elettrica
2 conduttori isolati formano un condensatore. I 2 conduttori si definiscono ARMATURE del
condensatore
Un condensatore e’ carico quando e’ presente una carica +q e -q rispettivamente sulle 2
armature
Le armature sono superfici equipotenziali.
Esiste quindi una differenza di potenziale ΔV (per comodita’ d’ora in poi indicheremo con V)
legata alla carica presente alle armature da una relazione di proporzionalita’:
q = CV
dove C = capacita’ elettrica
q
[C]
C=
=
= [F ] F arad
V
[V ]
Carica di un condensatore
collegando il condensatore con un circuito elettrico ad una batteria lo possiamo caricare
circuito elettrico:
e’ un percorso attraverso cui puo’ fluire una carica elettrica
batteria:
e’ un dispositivo in grado di mantenere una ddp costante tra
i suoi “poli”
Carica di un condensatore
Quando il circuito e’ “chiuso” la batteria fornisce il lavoro
necessario a muovere le cariche, instaurando un campo
elettrico E
Gli elettroni si spostano da h al polo positivo della batteria e
h si carica positivamente
Un numero uguale di elettroni lasciano il polo negativo e si
dirigono verso l che si carica negativamente
Ora i poli della batteria e le armature corrispondenti sono
allo stesso potenziale e le cariche non si muovono piu’
Il condensatore e’ completamente carico con carica q e ddp V
Calcoliamo la capacita’ elettrica
1) C’e’ una carica q sulle armature
2) Si calcola il campo E tra le armature
3) Da E si ricava la ddp V tra le armature
4) Si ricava C
calcolo del campo E
usiamo il teorema di Gauss
�0
�
� · dA
� = qint q = �0 EA
E
calcolo della ddp V
Vf − V i = −
V =
�
�
f
i
f
Eds
i
� · d�s
E
1) per superfici per cui E e dA sono
paralleli
2) E costante
su un qualunque percorso tra le armature da
quella negativa a quella positiva, cosicche’ E e ds
hanno verso opposto e V (=Vf-Vi) e’ definito
positivo
condensatore piano
consideriamo la superficie gaussiana
in figura
q = �0 EA
V =
�
f
Eds = E
i
q
�0 A
C=
=
V
d
�0 = 8, 85 · 10−12 C 2 /N · m2 → F/m
�0 = 8, 85 pF/m
�
d
ds = Ed
0
condensatore cilindrico
2 cilindri lunghi L, coassiali, di raggio a e b
scelgo una superficie gaussiana chiusa una cilindrica di
raggio r
q = �0 EA = �0 E(2πrL)
q
E=
2π�0 rL
V =
�
+
−
q
Eds = −
2π�0 L
L
C = 2π�0
ln(b/a)
�
a
b
dr
q
b
=
ln( )
r
2π�0 L
a
condensatore sferico
uso l’immagine di prima, consideratele come 2 sezioni
sferiche di raggio a e b
q = �0 EA = �0 E(4πr2 )
1 q
E=
4π�0 r2
V =
�
+
−
q
Eds = −
4π�0
ab
C = 4π�0
b−a
�
a
b
dr
q
=
2
r
4π�0
�
1 1
−
a b
�
osservazione: sfera carica isolata di raggio R
a
C = 4π�0
, b→∞
1 − a/b
C = 4π�0 R
(a = R)
condensatori in parallelo
tutti i condensatori sono soggetti alla stessa
differenza di potenziale V
sono quindi analoghi ad un unico
condensatore con carica totale pari alla
somma delle cariche:
q1 = C1V q2 = C2V q3 = C3V
qT = q1+q2+q3 = (C1+C2+C3)V
CT ot =
�
i
Ci
condensatori in serie
la differenza di potenziale ai capi dei singoli condensatori
stabilisce la stessa carica q
la differenza di potenziale applicata e’ la somma delle Vi ai capi dei
singoli Ci
perche’ hanno la stessa carica ?
1) attacchiamo la batteria
2) l’armatura inferirore di C3 si carica -q
3) questa carica “respinge” quelle negative dell’armatura superiore
inducendo la carica +q
4) le cariche allontanate finiscono sull’armatura inferiore di C2
ecc...ecc...
La batteria instaura una carica solo sull’armatura inferiore di C3 e
su quella superiore di C1, tutto il resto e’ induzione
condensatori in serie
piu’ condensatori in serie equivalgono ad un unico condensatore
con la medesima carica q sottoposto ad una ddp V pari alla
somma delle ddp
V1 = q/C1
V2 = q/C2
V3 = q/C3
V = V1 + V2 + V3 = q(1/C1 + 1/C2 + 1/C3)
CTot = q/V
1/CTot = (1/C1 + 1/C2 + 1/C3)
1
CT ot
� 1
=
Ci
i
energia immagazzinata nel campo elettrico
la carica viene posta nel condensatore ad opera di un agente esterno che compie del lavoro
la batteria compie lavoro che viene immagazzinato nel condensatore sotto forma di energia
potenziale U associata al campo elettrico tra le armature
questa puo’ essere riutilizzata scaricando il condensatore
Partiamo da un istante in cui sul condensatore sia gia’ presente della carica q e calcoliamo il
lavoro necessario a portare un’altra carica dq sulle armature
q
dL = V dq = dq
C�
�
1 Q
Q2
L = dL =
qdq =
C 0
2C
Q2
1
U=
= CV 2
2C
2
defibrillatore
200 J vengono scaricati con un impulso molto
breve ~ 2 ms
(carica a 200 - libera!)
1
1
2
U = CV = (70 · 10−6 F )(5000V ) = 875 J
2
2
U
200J
P =
=
= 100 kW
−3
t
2 · 10
densita’ di energia
u = energia/unita’ di volume
U
CV 2
u=
=
Ad
2Ad
per un condensatore piano
1 V 2
u = �0 ( )
2
d
q
�0 A
C=
=
V
d
cioe’
1
u = �0 E 2
2
se esiste un campo elettrico E in un certo punto dello spazio e’ associata a quel punto una
certa quantita’ di energia
condensatori e dielettrici
Faraday, 1837
se riempiamo lo spazio tra le armature di un condensatore con un isolante, un dielettrico
Faraday osserva tramite gli strumenti:
la capacita’ aumenta di un fattore εr
(costante dielettrica relativa del
materiale introdotto rispetto al
vuoto)
La ddp massima VMAX, che puo’
essere applicata tra le armature
oltre il quale il mezzo diventa
conduttore (cioe’ scarica) aumenta
a) la carica aumenta (la batteria manda altre cariche) a parita’ di V
b) la carica rimane costante, la ddp diminuisce
In una regione dove e’ presente un dielettrico tutte le leggi dell’elettrostatica viste fino
ad ora continuano ad essere valide sostituendo:
�0 → �0 �r
1
q
E=
4π�0 �r r2
interpretazione atomica
dielettrici polari/non polari
i condensatori nei banchi di memoria RAM hanno, tipicamente,
una capacita’ di 55 fF.
Se vengono caricati con potenziali dell’ordine di 5.3 V, quanti
elettroni in eccesso ci sono sulle armature ?
i condensatori nei banchi di memoria RAM hanno, tipicamente,
una capacita’ di 55 fF.
Se vengono caricati con potenziali dell’ordine di 5.3 V, quanti
elettroni in eccesso ci sono sulle armature ?
q
CV
(55 · 10−15 F )(5, 3V )
6
n= =
=
=
1,
8
·
10
e
e
1, 6 · 10−19
qual e’ la capacita’ equivalente del sistema di 3 condensatori in
figura se:
C1 = 12 uF
C2 = 5,3 uF
C3 = 4,5 uF
qual e’ la capacita’ equivalente del sistema di 3 condensatori in
figura se:
C1 = 12 uF
C2 = 5,3 uF
C3 = 4,5 uF
C12 = C1 + C2 = 12, 0µF + 5, 3µF = 17, 3µF
qual e’ la capacita’ equivalente del sistema di 3 condensatori in
figura se:
C1 = 12 uF
C2 = 5,3 uF
C3 = 4,5 uF
1
C123
1
1
1
1
=
+
=
+
= 0, 28µF −1
C12
C3
17, 3µF
4, 5µF
C123 = 3, 57µF
se si applica una ddp V = 12,5 V, qual e’ la carica su C1 ?
se si applica una ddp V = 12,5 V, qual e’ la carica su C1 ?
q123 = C123 V = (3, 57 µF )(12, 5V ) = 44, 6µC
se si applica una ddp V = 12,5 V, qual e’ la carica su C1 ?
C12 e C3 hanno la
stessa carica di C123
la ddp ai capi di C12 sara’:
V12
q12
=
= (44, 6 µC)(17, 3µF ) = 2, 58V
C12
se si applica una ddp V = 12,5 V, qual e’ la carica su C1 ?
C1 e C2 sono
soggetti alla stessa
ddp
q1 = C1 V1 = (12µF )(2, 58V ) = 31, 0 µC
su una sfera conduttrice isolata di raggio R = 6,85 cm e’ collocata una
carica q =1,25 nC
quanta energia potenziale e’ immagazzinata nel campo elettrico generato
dal conduttore ?
su una sfera conduttrice isolata di raggio R = 6,85 cm e’ collocata una
carica q =1,25 nC
quanta energia potenziale e’ immagazzinata nel campo elettrico generato
dal conduttore ?
q2
q2
U=
=
= 103 nJ
2C
8π�0 R
su una sfera conduttrice isolata di raggio R = 6,85 cm e’ collocata una
carica q =1,25 nC
qual e’ la densita’ di energia sulla superficie della sfera ?
su una sfera conduttrice isolata di raggio R = 6,85 cm e’ collocata una
carica q =1,25 nC
qual e’ la densita’ di energia sulla superficie della sfera ?
1
u = �0 E 2
2
1 q
E=
4π�0 R2
q2
3
u=
=
24,
4
µJ/m
32π 2 �0 R4
sulla superficie della
sfera