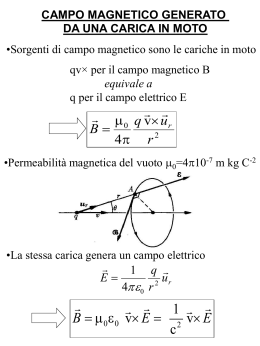
TERZA LEZIONE (4 ore):
INTERAZIONE MAGNETICA
•Evidenza dell’interazione magnetica; sorgenti delle
azioni magnetiche; forze tra poli magnetici, il campo
magnetico
•Forza magnetica su una carica in moto; particella
carica in moto in un campo magnetico
•Spettrometro di massa, ciclotrone
•Campo magnetico generato da una carica puntiforme
in moto; confronto tra interazione magnetica e
interazione elettrica;
•Il dipolo magnetico; azioni meccaniche su un dipolo
magnetico in campo magnetico esterno;
•Definizione di corrente elettrica; la corrente elettrica
in un conduttore; la densità di corrente;
•La legge di Ohm e la conducibilità;
•La potenza elettrica;
•Esercizi, leggi di Kirchoff, resistori in serie e parallelo;
INTERAZIONE MAGNETICA
Dall’analisi delle forze che si scambiano delle
sbarrette di alcuni minerali di ferro (dopo aver
escluso la natura gravitazionale o elettrica
delle interazioni) si introduce una nuova proprietà
della materia: IL MAGNETISMO
Nelle sbarrette il MAGNETISMO appare concentrato
agli estremi, che vengono chiamati poli magnetici.
Dalla attrazione o repulsione dei poli si deduce
l’esistenza di due tipi di poli magnetici: NORD e SUD
L’interazione tra poli magnetici uguali e repulsiva,
mentre l’interazione tra poli diversi è attrattiva.
Si potrebbe sviluppare un discorso analogo a quello
visto con la carica elettrica.
Cioè introdurre:
l’equivalente di una carica magnetica e
l’equivalente della Legge di Coulomb
per il magnetismo
STORICAMENTE SI E’ FATTO COSI’
FORZA MAGNETICA
SU UNA CARICA IN MOTO
Sperimentalmente si osserva che:
•una carica elettrica in quiete posta in un campo
magnetico non subisce alcuna forza;
•una carica elettrica che si muove con una velocità v
in una regione ove esiste un campo magnetico B
subisce una forza
di modulo proporzionale alla
carica e alla componente della velocità perpendicolare
al campo magnetico, di direzione perpendicolare al
piano definito dal vettore velocità della carica e dal
campo magnetico, di verso dato dalla regola della
mano destra.
In formula tale forza è esprimibile come:
F = qv × B
In modulo la forza vale:
F = qvBsinα
Tramite questa relazione è definibile l’unità di
misura del campo magnetico:
Ns
nel S.I. [ B ] =
= Tesla
Cm
Particella carica in moto in un
campo magnetico uniforme
1) Consideriamo una particella di carica q in moto
con vettore velocità v perpendicolare al vettore
campo magnetico B uniforme.
La forza è sempre perpendicolare alla velocità.
F = qv × B
F ⋅ v = potenza = 0
Quindi la direzione di v cambia ma il modulo
rimane costante.
Infatti il campo magnetico non compie lavoro,
non induce una variazione di energia cinetica, e
quindi non cambia v2 (ossia il suo modulo)
Si instaura quindi un moto circolare uniforme con
2
v
F qvB
acc. centripeta =
= =
r m
m
Quindi
il raggio dell’orbita è:
mv
r=
qB
La velocità angolare è
v
; con ω =
r
q
ω = B
m
detta frequenza ciclotronica
2) Se la carica q entra nel campo magnetico uniforme
con direzione non perpendicolare al campo,
il vettore velocità può essere scomposto in
(i) una componente parallela al campo
(che non viene modificata)
(ii) una componente perpendicolare al campo
(che cambia direzione).
Il moto risultante è un’ elica
ESEMPI
1)
Lo spettrometro di massa
F = qv × B
mv
q
r=
v = Br
qB
m
1 2
q
2
mv = q∆V
v = 2 ∆V
2
m
q
2
= 2 2 ∆V
m B r
mel=9.1 1031 Kg
2
Campo magnetico generato da una carica in moto
Le sorgenti del campo magnetico sono le cariche
elettriche in moto. Sperimentalmente si è verificata
la seguente legge per il campo generato da una
carica q in moto con velocità v:
µ0 è detta permeabilità magnetica
del vuoto e vale nel S.I.
µ 0 qv × u r
µ0 = 4π
π 10-7 m kg C-2
B=
4π
r
2
Ricordando che la stessa
carica genera un campo elettrico
Si vede che
1 q
E=
ur
2
4 πε 0 r
1
B = µ0 ε0 v × E = 2 v × E
c
µ 0 qv × u r
B=
2
4π r
N. B. 2 osservatori in moto relativo
misureranno velocità della carica
diverse e quindi campi magnetici
diversi
Confronto tra interazioni elettrica e magnetica
Vediamo di confrontare l’ordine di grandezza della
interazione magnetica con quella elettrica.Prendiamo due
cariche q e q’ con velocità v e v’ rispetto un sistema inerziale.
q
v
q’
v’
La forza magnetica tra le cariche è
C.M. dovuto a q’ C.E. dovuto a q’
Forza magn. agente su q
FM = qvB =
vv'
qE
2
c
La forza elettrica agente sulla carica q è
FE = qE
FM
vv'
= 2
FE
c
Se prendiamo gli elettroni
in un atomo hanno velocità
dell’ordine di 105 m/s
FM
≈ 10-7
FE
CORRENTI ELETTRICHE
La corrente elettrica è un flusso di particelle cariche.
L’intensità di una corrente è definita come la quantità
di carica netta che attraversa nell’unità di tempo una
superficie:
∆Q
I=
∆t
L’unità di misura di I nel S.I è C/s detta Ampere (A)
LA CORRENTE ELETTRICA
IN UN CONDUTTORE
Prendiamo un filo conduttore di sezione S.
Nel conduttore ci sono n particelle cariche per
unità di volume, ognuna di carica q, in moto con
velocità v nella stessa direzione.
Attraverso la sezione in B passano nel tempo ∆t
le cariche contenute nel volume delimitato dalle
sezioni A e B
∆Q = nqSv∆t
∆Q
I=
= nqSv
∆t
Definendo la densità di corrente come la
corrente che passa per una superficie unitaria
I
j = = nqv
S
Tenendo conto che la velocità è un vettore
j = nqv
La densità di corrente nel S.I. si misura in A/m2
Legge di Ohm
In un materale conduttore (con elettroni liberi)
la presenza di un campo elettrico E dà origine ad
un moto ordinato degli elettroni che si sovrappone
al moto termico casuale.
A temperatura costante il rapporto tra la differenza di
potenziale fra due punti e la corrente elettrica è una
costante detta resistenza elettrica R (Legge di Ohm).
∆V=RI
Nel S.I. la unità di misura di R è l’OHM [Ω]
Ω]
Conducibilità elettrica
Se consideriamo un conduttore cilindrico di sezione S
e lunghezza l ai cui capi si pone una diff. di pot. ∆V
abbiamo:
∆V lE
I = jS =
=
R
R
l
j=
E = σE
RS
σ è detta
conducibilità elettrica
con unità di misura
nel S.I. (Ω
Ω m)-1
Possiamo mettere in relazione la conducibilità
e la resistenza elettrica:
l
R=
σS
1
Si definisce anche la resistività elettrica ρ =
σ
che nel S.I. si misura in Ω ·m
Tenendo poi conto delle due relazioni:
j = σE
j = nqv
si ottiene v =
σ
nq
⋅E
mobilità
v è la velocità di deriva degli elettroni dovuta al
campo elettrico.
Quindi i portatori di carica in un conduttore
raggiungono una velocità di deriva costante anche
se sono sottoposti alla forza del campo elettrico.
Si può quindi supporre l’esistenza di un meccanismo
di perdita di energia cinetica ---> urto con gli atomi.
Potenza elettrica
In un materiale conduttore l’energia fornita alle
cariche per tenerle in moto è persa negli urti con
gli atomi (sotto forma di calore, effetto Joule).
Supponiamo di voler spostare N cariche q nel tempo
∆t attraverso la diff. di pot. ∆V. L’energia per
unità di tempo (potenza, P) vale:
energia Nq∆V Q∆V
P=
=
=
∆t
∆t
∆t
P = I∆V = RI 2
E
v
∆V
E
v
∆V
P = I∆V = RI 2
Energia = P∆t = I∆t∆V = I∆t ⋅ RI
Se le cariche che costituiscono una corrente devono
percorrere un cammino chiuso (circuito), esse hanno
bisogno di energia per rimanere in moto nonostante
gli urti con il reticolo.
ENERGIA FORNITA = ENERGIA PERSA IN URTI
Q∆V
=
Q RI
da cui in un circuito deve essere fornita dall’esterno una
energia ∆V (detta forza elettro motrice fem) per
vincere la resistenza elettrica totale R
Esercizio
Vediamo di calcolare la resistività e la
velocità di deriva degli elettroni di un conduttore di
rame cilindrico in cui circola una corrente I=100 A.
densità elettronica 8.49 1028 elettroni/m3
diametro d=5 mm, lunghezza l=1 m
diff. di pot. applicata ai capi del filo V= 86 mV
velocità termica degli elettroni supposti
un gas ideale vt=(3kT/me)1/2=1.17 105 ms-1
velocità di deriva v=3.7 10 -4 m/s, t transito = 45 min!!!
resistività rame ρ=1.69 10-8 ohm m
Esercizio
In un materiale isolante si ricava una semisfera di raggio
r1 = 1 m, sulla cui superficie si deposita uno strato
conduttore, che viene riempita di un liquido con
ρ =5 × 10 10 Ωm.
Nel liquido si immerge un elettrodo emisferico di raggio
r2 = 0.5 m e concentrico con l'
altra emisfera. Determinare la
corrente che circola nel liquido quando è applicata una
tensione tra i due elettrodi V = 50 V.
resistenza totale R=80 GΩ
corrente I=6.3 pA
Avendo un insieme di conduttori
che costituiscono una rete elettrica complessa
i principi:
(i) di conservazione della carica elettrica
e (ii) conservazione dell’energia
(visto sotto forma di bilancio del potenziale o fem)
diventano le leggi di Kirchoff
1. La somma di tutte le correnti (entranti e
uscenti) da un nodo è nulla;
2. La somma di tutte le differenze di potenziale
lungo un qualsiasi percorso chiuso entro la rete
è nulla (si deve tenere conto sia dei generatori
di fem che delle perdite negli urti, resistenze)
I1
I3
R1
I
_
+
I
I5
I1+I2-I3+I4+I5=0
I1+I2=I3+I4+I5
I4
+
∆V
R2
_
∆V-∆V2-∆V1=0
∆V=∆V2+∆V1= R2·I+ R1·I
∆V2=V2+-V2-=R2·I
I2
∆V1=V1+-V1-=R1·I
Resistori in serie e in parallelo
Resistori Ri i=1,2,…N posti in serie o in parallelo
possono essere ridotti ad un resistore equivalente Req
serie
parallelo
Req =
1
=
Req
N
i =1
N
i =1
Ri
1
Ri