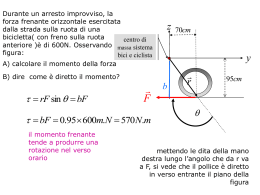
ESERCITAZIONI FISICA PER FARMACIA A.A. 2013/2014
ROTAZIONE, MECCANICA DEL CORPO RIGIDO
Esercizio 1
Un bimbo di massa m = 25 kg su una giostra si muove con una velocità di 1,25 m/s quando è a 1,10
m dal centro della giostra. Calcolare:
a) la velocità angolare del bimbo;
b) l’accelerazione del bimbo;
c) la forza orizzontale esercitata su di lui.
d) Qual è la velocità di un secondo bimbo posto a 2,3 m dal centro della giostra?
Esercizio 2
Una palla di 45 kg attaccata all’estremità di una corda orizzontale viene fatta roteare in una
circonferenza di raggio 1,3 m su una superficie priva di attrito. Se la corda si rompe quando la
tensione supera i 75 N, qual è la massima velocità che può avere la palla?
Nel caso in cui la palla ruoti con una velocità pari alla metà della velocità massima, calcolare quanti
giri compie la palla in 2 minuti.
________________________________________________________________________________
Esercizio 3
Le lame di un frullatore ruotano a una velocità di 108 rad/s. Quando il motore viene spento, le
lame rallentano fino a fermarsi in 3 s. Qual è l’accelerazione angolare quando le lame cominciano
a rallentare?
1
Esercizio 4
Una ruota del diametro di 70 cm accelera uniformemente attorno al suo centro da 2,2 rad/s a 4,7
rad/s in 4 s. Determinare:
a) la sua accelerazione angolare;
b) le componenti radiale e tangenziale dell’accelerazione lineare di un punto sul bordo della ruota
2 s dopo che essa ha iniziato ad accelerare.
c) Il numero di giri compiuti dalla ruota nei 4 secondi.
Esercizio 5
Un motore elettrico, che mantiene in rotazione una mola di momento di inerzia 4,8 kg m 2 alla
velocità di 10,5 rad/s, viene spento. Supponendo che la decelerazione angolare sia costante e pari
a 2,0 rad/s2, calcolare:
a)
l’energia cinetica rotazionale e il momento angolare della mola nell’istante in cui il motore
viene spento;
b)
il tempo impiegato dalla mola per fermarsi;
c)
il numero di giri effettuati dalla mola dopo 2 s dall’istante in cui il motore viene spento.
2
Esercizio 6
Una forza esterna e una forza di attrito dinamico, entrambe costanti, sono applicate ad una ruota
che gira attorno al suo asse. L’effetto risultante di queste due forze è un momento di 40 Nm
applicato alla ruota. La forza esterna agisce in 8 s e in questo intervallo di tempo la velocità
angolare della ruota passa da 0 a 12 rad/s. In questo istante, la forza esterna viene eliminata, e la
ruota si ferma in un intervallo di tempo Δt = 60 s. Calcolare:
a)
il momento di inerzia della ruota;
b)
il momento della forza di attrito;
c)
il lavoro effettuato dalla forza di attrito.
3
Esercizio 7
Una ragazza si accinge a fare una flessione, come mostrato in figura. Il suo centro di gravità si
trova in corrispondenza del punto P sul pavimento, che è a 0,9 m dai suoi piedi e a 0,6 m dalle sue
mani. Se la sua massa è 54 kg, qual è la forza esercitata sul pavimento dalle sue mani?
A
0,9m
P
0,6m
B
Esercizio 8
In una macchina di Atwood, come quella in figura, un blocco ha una massa M = 0,5 kg, l’altro m =
0,46 kg. La puleggia, montata su cuscinetti orizzontali privi di attrito, ha raggio 5 cm. Lasciato
libero da fermo, il blocco più pesante cala di 75 cm in 5 s, senza che il filo slitti sulla puleggia.
a) Qual è, in modulo, l’accelerazione di ciascun blocco?
b) Qual è la tensione nel tratto di filo che sostiene il blocco più pesante?
c) Qual è la tensione nel tratto di filo che sostiene il blocco più leggero?
d) Qual è in modulo l’accelerazione angolare della puleggia?
e) Qual è il suo momento di inerzia?
4
5