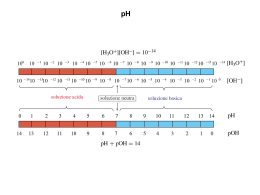
Acidi Deboli
Si definisce acido debole un acido con Ka < 1 che risulta perciò solo
parzialmente dissociato in soluzione.
Esempi di acidi deboli:
Acido acetico (CH3COOH) Ka = 1.75 × 10-5
Acido ascorbico (vitamina C) Ka1 = 6.76 × 10-5 Ka2 =2.5 × 10-12
Acido acetilsalicilico (aspirina) Ka = 3.2 × 10-4
Acido Carbonico H2CO3 Ka1 = 4.45 ×10-7 Ka2 = 4.69 × 10-12
Ione ammonio NH4+ Ka = 5.70 × 10-10
Dati ottenuti da Harris
Alcune di queste slides riportano materiale gentilmente concesso dal Dr.
Valerio Di Marco- Dip. Scienze Chimiche – Univ. Padova
1
Determinazione del pH in una soluzione di un acido debole monoprotico
La reazione di dissociazione acida è solo parziale:
HA (aq) + H2O (solv) = H3O+ (aq) + A− (aq)
In soluzione saranno quindi presenti le specie: HA, A¯ , H3O+, OH¯ (dall’equilibrio
di autoprotolisi). Per conoscere le concentrazioni di queste specie è necessario
trovare un sistema di quattro equazioni che leghino queste incognite:
K W = [H 3O + ][OH − ]
[A − ][H 3O + ]
Ka =
[HA]
Autoprotolisi dell’acqua
Costante di equilibrio di dissociazione acida
[OH − ] + [A − ] = [H 3O + ]
Bilancio di carica
[A − ] + [HA] = C 0HA
Bilancio di massa (C0HA è la concentrazione
di acido inizialmente sciolta)
Risolvendo questo sistema rispetto a [H3O+] (posta uguale a x) si ottiene
un’equazione di terzo grado in questa incognita:
(
)
x 3 + K a x 2 − K w + K a C0HA x − K w K a = 0 x = [H 3O + ]
2
Questa equazione si può risolvere numericamente con un foglio elettronico.
Ad esempio se Ka = 1.75 ×10-5 (acido acetico) e C0HA = 0.01 M
1e-10
1e-11
5e-11
f(x)
f(x)
5e-12
0
0
-5e-12
-5e-11
-1e-11
0.00030
-1e-10
-0.0010
-0.0005
0.0000
0.0005
0.00040
0.00045
0.00050
x
0.0010
x
[H3O+] = 4.097·10–4 M
0.00035
x = 0.0004097
pH = 3.39
[OH–] = 10–14/[H3O+] = 2.441·10–11 M
[A–] = [H3O+] – [OH−] = 4.097·10–4 M
[HA] = 0.01 – [A−] = 9.590·10–3 M
3
E’ possibile arrivare allo stesso risultato, entro una precisione del 5%,
facendo però un’approssimazione che riduce l’equazione precedente ad
un’equazione di secondo grado.
Trascuro [OH–] nel bilancio di carica dove appare come termine additivo,
supponendo che sia molto piccolo. Rimangono allora solo tre variabili e sono
sufficienti tre equazioni:
[ A− ][ H 3O + ]
Ka =
[ HA]
[ A− ] = [ H 3O + ]
0
[ A− ] + [ HA] = C HA
Da cui si ottiene una semplice equazione di secondo grado:
x = [ H 3O + ]
−5
[H3
O+]
=
− 1.75 ⋅10 ±
0
x 2 + K a x − K a C HA
=0
(1.75 ⋅10 )
−5 2
2
+ 4 ⋅1.75 ⋅10
0.0004097
−7
=
–0.000427
4
Soluzione di un’equazione di secondo grado generica:
ax 2 + bx + c = 0
− b ± b 2 − 4ac
x=
2a
Matematicamente l’equazione ha due soluzioni, di cui una sola però ha significato
fisico, per cui si sceglie quella con significato fisico (in questo caso quella positiva
perché non ha significato fisico una concentrazione negativa)
5
Per verificare se l’approssimazione introdotta è corretta, si sostituiscono i risultati
ottenuti nell’equazione approssimata, e si valuta se il termine trascurato fosse
veramente approssimabile
Regola adottata per le approssimazioni:
un termine additivo A può essere approssimato rispetto ad un
altro termine B se A è minore o uguale al 5% del valore di B
[H3O+] = [OH–] + [A–]
4.097·10–4 = 2.441·10–11 + 4.097·10–4
Per esempio, in questo caso [OH–] è lo 0.000006%
rispetto ad [A–], quindi l’approssimazione è corretta
Commento: la regola del 5% viene adottata in questo corso per dare una stima
delle quantità trascurabili. Quando si lavora in campo analitico la tolleranza da
imporre dipende da vari fattori (precione richiesta, eprciollosità di una sostanza,
etc.etc.) e deve essere scelta in modo opportuno.
6
E’ possibile fare un’ulteriore approssimazione: poiché l’acido è debole,
l’equilibrio è spostato verso i reagenti, per cui possiamo ipotizzare che anche la
concentrazione di A– sia trascurabile come termine additivo nel bilancio di massa
[ A− ][ H 3O + ]
Ka =
[ HA]
[ A − ] = [ H 3O + ]
0
[ HA] = C HA
In questo caso:
0
0
x 2 − K a C HA
= 0 x = K a C HA
= [ H 3O + ]
pH =
1
1
0
pK a − log10 C HA
2
2
L’approssimazione di [A–] è possibile se (all’incirca)
C0HA > 100·Ka
E comunque va sempre verificata con la regola del 5%
7
Reazioni acido-base
Grafico: pH di un ac. debole in funzione della sua conc. iniziale C0HA
esempio dell’acido acetico (Ka = 1.75·10–5, pKa = 4.76)
C0HA>100·Ka
C0HA<0.1·Ka
7
6
[H O ] =
5
pH
Quando l’acido è molto diluito tende a
essere completamente dissociato
+
3
Da qui in poi, andamento pH
vs. -logC0HA è simile a quello
dell’acido forte
0
HA
C Ka
4
3
pH=½pKa
Ciò accade se (circa!) C0HA < 0.1·Ka
[H O ] =
+
2
3
0
− K a + K a2 + 4 K a CHA
2
1
0
0
1
2
3
4
5
6
7
8
9 10 11 12
0
0
− log
pC
10 C
HA
HA
8
Perché a basse concentrazioni l’acido debole tende a essere
completamente dissociato?
Frazione di dissociazione di un acido debole
Si definisce frazione di dissociazione α di un acido debole il rapporto tra la
concentrazione di acido dissociato e la concentrazione iniziale di acido posta
in soluzione (concentrazione analitica)
HA (aq) + H2O (solv) = H3O+ (aq) + A‒ (aq)
[A − ]
[A − ]
α= 0 =
CHA [HA] + [A − ]
• La frazione di dissociazione aumenta al diminuire della concentrazione
analitica di acido debole.
• La frazione di dissociazione è tanto più grande quanto più grande è la
Ka
9
Frazione di dissociazione percentuale di un acido debole
Spesso la frazione di dissociazione α di un acido viene riportata in maniera
percentuale, ovvero il valore di α viene moltiplicato per 100 e indicato con il
simbolo %
[A − ]
[A − ]
α = 0 × 100 =
× 100
−
[HA] + [A ]
CHA
Esempio: Per l’acido acetico (Ka= 1.7 x 10-5 M) si considerano le seguenti
concentrazioni analitiche:
C0= 0.01 M, C0 =1 x 10-4 M e C0=1x10-6 M:
Risolvendo con le formule precedenti il problema all’equilibrio si ottiene:
0
C HA
= 0.01 M
[ H 3O + ] = [A − ] = C 0HA K a = 4.12 × 10 −4 M
[A − ]
α = 0 = 0.04 ×100 = 4%
CHA
10
0
C HA
= 0.0001 M
− K a ± K a2 + 4C 0HA K a
[ H 3O ] = [ A ] =
= 3.36 × 10 −5 M
2
[A − ]
α = 0 = 0.34 × 100 = 34%
CHA
+
−
0
C HA
= 0.000001 M
− K a ± K a2 + 4C 0HA K a
= 9.48 × 10 − 7 M
[ H 3O ] = [ A ] =
2
[A − ]
α = 0 = 0.94 × 100 = 94%
CHA
+
−
11
Riportando in grafico i valori di α in funzione della concentrazione iniziale
decrescente per l’acido acetico con Ka = 1.7x10-5 si ottiene un andamento
crescente, come mostrato nella figura
α
0
C HA
= 0.01
α = 4%
0
C HA
= 0.0001
C
0
HA
= 0.000001
α = 34%
α = 94%
100
80
60
40
Al diminuire della
concentrazione
l’acido si dissocia sempre di
più, fino a risultare
completamente dissociato alle
basse concentrazioni come nel
caso degli acidi forti.
20
0
10-1
10-2
10-3
10-4
10-5
10-6
10-7
[HAc]0
12
Effetto della Ka sul pH di un acido debole in funzione
della sua concentrazione iniziale C0HA
L’acido con Ka = 10–3 è pochissimo dissociato per (circa) C0HA > 10–1 ed è tutto
dissociato (è acido forte) per (circa) C0HA < 10–4
L’acido con Ka = 10–7 è pochissimo dissociato per (circa) C0HA > 10–5 ed è tutto
dissociato (è acido forte) per (circa) C0HA < 10–8.
Ka = 10–3
Ka = 10–7
6
5
pH
4
3
2
1
7
pochissimo dissociato
7
6
5
tutto dissociato
pH
4
tutto
dissociato
pochissimo
dissociato
3
2
1
0
0
0
1
2
3
4
5
6
pC0HA
7
8
9 10 11 12
0
1
2
3
4
5
6
pC0HA
7
8
9 10 11 12
13
13
Riassumendo:
Calcolo del pH per soluzioni contenenti un acido debole, di cui sono dati la sua
C0HA e la sua Ka. Il calcolo è indipendente dalla carica dell’acido.
– se (circa) C0HA > 100·Ka, l’acido è pochissimo dissociato, ed è:
+
[H 3O ] = K a C
oppure
0
HA
pH =
1
1
0
pK a + pCHA
2
2
– se (circa) C0HA < 0.1·Ka, l’acido è tutto dissociato, cioè si comporta da
acido forte
– se C0HA è intermedio, l’acido è apprezzabilmente ma non tutto
dissociato. E’ necessario risolvere il sistema approssimando solo
[OH–], oppure ricordare la formula:
2
0
−
K
+
K
+
4
K
C
a
a
a HA
H 3O + =
2
[
]
14
Acido debole carico positivamente AH+:
Caso tipico: NH4+, ione ammonio, che viene introdotto in soluzione come sale
(associato ad un controione che non dà reazioni acido-base). Ad esempio,
NH4Cl.
In generale per un composto generico AHD:
AHD (s) = AH+ (aq) + D‒ (aq)
AH+(aq) + H2O (solv) = A (aq) + H3O+ (aq)
Supponiamo che la concentrazione iniziale di AHD sia C0AHD e che AH+ sia
un’acido debole con costante di dissociazione Ka. Inoltre D− non dà reazione
acido base con l’acqua
Trascurando l’acqua come solvente, le specie presenti in soluzione sono:
[AH+], [A], [D−], [H3O+], [OH−], quindi servono 5 equazioni in 5 incognite:
15
K W = [H 3O + ][OH − ]
[A][H3O + ]
Ka =
[AH + ]
[OH − ] + [D − ] = [H 3O + ] + [AH + ]
Bilancio di carica
[A] + [AH + ] = C 0AHD
[D − ] = C0AHD
Bilanci di massa
Nel bilancio di carica trascuro [OH−] perché la soluzione sarà acida.
Ponendo sempre nel bilancio di carica [ AH + ] = C 0AHD − [ A ] e [ D − ] = C 0AHD
Si ottiene:
[A] = [H 3O + ]
E quindi:
Se C 0HA > 100 K a
[H 3O + ] = [A] = K a C 0AHD
Se C
0
HA
< 100 K a
2
0
−
K
±
K
+
4C
a
a
AHD K a
+
[H 3O ] = [A] =
2
Infine:
[OH − ] =
Kw
[H 3O + ]
[AH + ] = C 0AHD − [A]
16