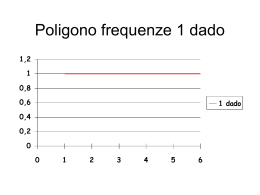
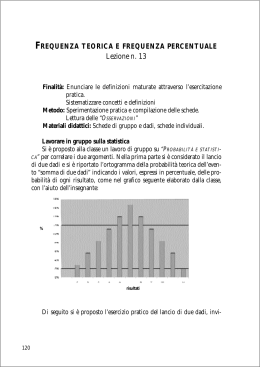
RICONOSCIMENTO AUTOMATICO
DI DADI DA GIOCO TRAMITE
IMAGE PROCESSING
Stefano Schillani
CdLS in Ingegneria Elettronica
Università degli Studi di Trieste
Corso: Elaborazione Elettronica delle
Immagini II (A.A. 2011/2012)
Docente: prof. Gabriele Guarnieri
Introduzione



I dadi hanno una distribuzione di probabilità
discreta uniforme e vengono solitamente utilizzati
in qualsiasi ambito in cui sia necessario
determinare uno possibile tra più esiti
equiprobabili in maniera casuale (es: giochi,
diceware...)
Sono più affidabili di algoritmi pseudo-casuali
Solitamente i risultati vengono determinati per
ispezione visiva da parte di un operatore (es:
casinò, giochi da tavolo, wargame...)
Obiettivo

Riconoscere da una fotografia il risultato del
lancio di una serie di dadi
3, 2, 6, 3, 1, 3, 5, 3
Problematiche

Legate all'immagine


Legate all'acquisizione


Illuminazione, ombre, tipo di dadi...
Risoluzione immagine, altezza e angolazione
macchina fotografica...
Legate all'algoritmo

Complessità computazionale...
Scelta delle condizioni


Si può supporre di operare all'interno di una
macchina predisposta

Altezza della fotocamera fissata per semplificare
l'algoritmo → valido anche su un tavolo da gioco

Illuminazione “decente” e sfondo nero per
ridurre ombre e riflessi → abbastanza
riproducibile in una sala da casinò
Dadi noti

Dadi uguali tra loro

Dadi bianchi a pallini neri tutti uguali
Scelta delle condizioni

Risoluzione immagine


L'algoritmo deve poter accettare immagini a
risoluzioni diverse
Complessità computazionale

Per trovare i dadi si usa una versione
ridimensionata dell'immagine di partenza

Si cercano i pallini su sottoinsiemi dell'immagine
originale
Descrizione dell'algoritmo
Preprocessing



Riduzione immagine a 1152x864
Aggiustamento costanti di lavoro degli operatori
morfologici
Filtraggio rumore e binarizzazione dell'immagine
ridotta
Trovare i dadi

I dadi sono regioni quadrate, ma dadi vicini
possono produrre regioni contigue e una semplice
apertura potrebbe non funzionare

Erosione complessiva → Segmentazione →
Dilatazione delle singole regioni
Trovare i dadi

Una singola regione è quadrata (cioè è un dado)
quando il rapporto tra perimetro al quadrato e area
è vicino a 16


Perimetro2 / Area ~ (4L)2 / L2 = 16
Una volta trovato un dado, occorre delimitare la
zona corrispondente

Scorrendo sui vettori delle somme per colonne e
per righe, si cercano i primi e gli ultimi elementi
diversi da zero, che corrispondono alle 4
coordinate estreme della regione
Trovare i pallini


Ritaglio immagine
originale in base alle
coordinate del dado
Riduzione rumore,
binarizzazione,
mascheratura tramite
intersezione,
complemento, apertura,
segmentazione
Trovare i pallini

Una singola regione è circolare (cioè è un pallino)
quando il rapporto tra perimetro al quadrato e area
è vicino a 4π

Perimetro2 / Area ~ (r2π)2 / r2π= 4π
Risultati e conclusioni


L'algoritmo è stato testato su 12 immagini di
diverse dimensioni per un totale di 86 dadi senza
compiere errori
L'attendibilità raggiunta è del 100%
Sviluppi Futuri




Altezza variabile (es:
cellulare)
Illuminazione variabile
(es: retinex)
Sfondo variabile
Segmentazione per
colore (es: i dadi rossi
hanno un significato
diverso dai dadi neri)
Bibliografia



Chin-Ho Chung, Wen-Yuan Chen, Bor-Liang Lin,
“Image Identification Scheme for Dice Game”,
2009 International Conference on Advanced
Information Technologies (AIT) 2009, pp. 144150, 24-25 April. 2009.
Wen-Yuan Chen, Pei-Jung Lin, Dong-Yi Kuo,
“Dice image Recognition Scheme Using Pattern
Comparison Technique”, 2012 International
Symposium on Computer, Consumer and Control
http://world.std.com/~reinhold/diceware.html