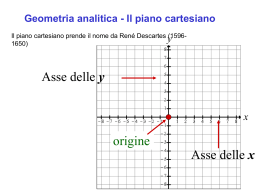
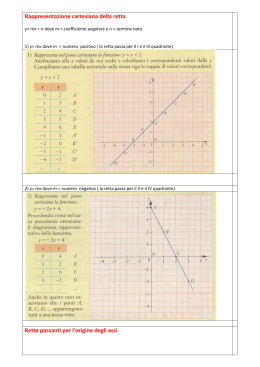
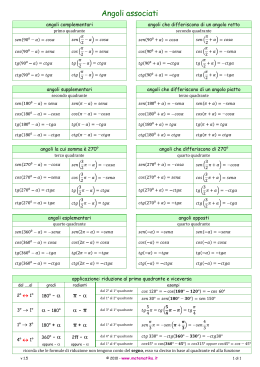
IL PIANO CARTESIANO
Prof.ssa A. Sia
Il piano cartesiano è individuato da due rette
perpendicolari (ortogonali) che si incontrano in un
punto O detto origine del piano cartesiano.
0
Prof.ssa A. Sia
Si fissa la stessa unità di misura su
entrambe le rette a partire dall’origine
O. le rette vengono così dette
monometriche.
-La retta orizzontale prende
il nome di asse delle x o
delle ascisse, e la retta
verticale prende il nome di
asse delle y o delle ordinate.
-I due assi individuano quattro angoli
che prendono il nome di quadranti che
vengono numerati a partire da quello
in alto a destra.a e procedendo
Prof.ssa A. Sia
Ogni punto del piano cartesiano individua
una coppia di numeri sugli assi cartesiani
individuata tracciando le distanze (i
segmenti di perpendicolare) del punto
degli assi. Ogni coppia ordinata di numeri
individua un punto nel piano cartesiano e
quindi si dice che esiste una
corrispondenza biunivoca tra punti del
piano e coppie ordinate di numeri.
II Quadrante x<0
Y>0
III Quadrante x<0
Y<0
Prof.ssa A. Sia
I Quadrante x>0
Y>0
IV Quadrante x>0
Y<0
•Nel secondo
quadrante i punti
hanno la prima
coordinata negativa
e la seconda positiva
-vedi ad esempio il
punto B(-4,2)
•Nel terzo
quadrante i punti
hanno entrambe le
coordinate negative
-vedi ad esempio il
punto C(-5,-3)
Prof.ssa A. Sia
•Nel primo quadrante i
punti hanno entrambe le
coordinate positive
-vedi ad esempio il punto
A(2,3)_
•Nel quarto quadrante i
punti hanno la prima
coordinata positiva e la
seconda negativa
-vedi ad esempio il
punto D(3,-4)
Vogliamo ora calcolare la distanza
assoluta tra due punti del piano nel
quale sia fissato un sistema di
riferimento di coordinate cartesiane
ortogonali. Siano A(x1,y1) e B(x2,y2)
i due punti dati. Osservando la figura
si nota che:
Applicando il teorema di Pitagora…..
Allora anche..
Prof.ssa A. Sia
Casi Particolari
Se i due punti hanno ascissa uguale, oppure ordinata uguale
ritroviamo ancora rispettivamente
Allineati orizzontale
Allineati verticale
Infine la distanza di un punto A(x) dall’origine O(0,0) sarà
Prof.ssa A. Sia
Vogliamo trovare le coordinate del punto medio M di un segmento, i
cui estremi sono i punti A(xA,yA) e B(xB,yB).
Coordinate punto Medio del segmento di estremi A B
Lo stesso procedimento ci
permette di risolvere anche il
problema di trovare il
simmetrico di un punto rispetto
ad un punto dato. Supponendo
noti A e M vogliamo ad esempio
ricavare B. Le formule
precedenti diventano allora:
Prof.ssa A. Sia
Prof.ssa A. Sia