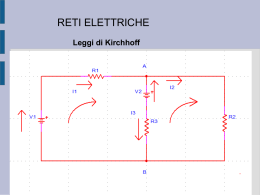
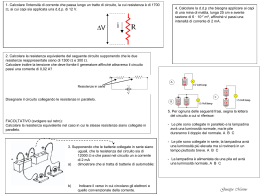
Strategie per la risoluzione di
problemi sui circuiti elettrici
Le leggi di Kirchhoff
Gustav Kirchhoff , Germania, (1824 – 1887)
Le due leggi di Kirchhoff , che vedremo in dettaglio di
seguito, non sono altro che un modo particolare per
esprimere la conservazione della carica (legge dei nodi)
e la conservazione dell’energia (legge delle maglie).
In
parallelo
Primo metodo
Per analizzare un circuito
che presenta più resistenze
ed è alimentato da uno o
più generatori, occorre
esaminare
tutti
i
collegamenti e riconoscere
gruppi di resistenze in
serie e in parallelo.
Successivamente occorrerà
sostituirli con le rispettive
resistenze equivalenti.
R
+
-
R1
R2
R
R
+
-
Req
R
In serie
Primo metodo: le resistenze
equivalenti
Ridisegnare
il
circuito
semplificato ed applicare la
legge della maglia:
“La somma algebrica di tutte le
differenze di potenziale lungo
una maglia chiusa in un circuito
è nulla.”
f – R’eq * i = 0
+
-
R’eq
-
Se al termine di questo
procedimento il circuito
presenta ancora due o
più maglie,
(come esempio in figura)
assegna un verso alle
correnti il ciascun ramo
del
circuito
(tratto
compreso tra due nodi)
e indica i versi nel
diagramma.
+
Secondo metodo
+
R
R
R
Secondo metodo
-
+
9V
15 V
+
-
Nell’esempio raffigurato
si possono evidenziare
due maglie e due nodi.
100 
100 
100 
-
+
9V
15 V
15 V
+
-
100 
100 
100 
Secondo metodo
Maglia 1
-
+
Per studiare il circuito,
cioè conoscere le
correnti
che
attraversano
ciascun
ramo, applichiamo la
legge dei nodi:
“la somma algebrica di
tutte le correnti entranti
(+) e uscenti (-) in un
nodo di un circuito deve
essere uguale a zero.”
E la legge delle maglie
già citata.
Nodo
A
15 V
+
-
100 
100 
100 
Maglia 2
Nodo
B
Secondo metodo
A
Legge della maglia 1
15 - RI3- RI1 = 0
+
Si ottengono tre equazioni
indipendenti con tre incognite,
cioè le tre correnti.
I2
I3
100 
-
Legge della maglia 2
-9 – RI2 + RI3 = 0
I1= 0,07 A
I2= -0,01 A
I3 = 0,08 A
I1
15 V
100 
-
Legge dei nodi in A
I1- I2- I3 = 0
+
9V
100 
B
La corrente I2 risulta negativa, questo vuol dire che
la sua direzione è opposta a quella mostrata in
figura.
Esegui l’esercizio seguente
A
1,0 
7,1 
4,5 
3,2 
r
-
5,8 
+
Il circuito in figura comprende una
batteria dotata di una resistenza
interna r = 0,050 .
• Calcola la corrente che attraversa
le resistenze da 7,1  e 3,2 
rispettivamente.
• Qual è l’intensità della corrente
che scorre nella batteria?
• Qual è la differenza di potenziale
tra i terminali della batteria?
B
12,0V
Risultati: i7,1 = 0,28 A ; i3,2 = 1,1 A ; ib = 1,4 A .